Question
Let \(f:x \mapsto {\sin ^3}x\) .
(i) Write down the range of the function f .
(ii) Consider \(f(x) = 1\) , \(0 \le x \le 2\pi \) . Write down the number of solutions to this equation. Justify your answer.
Find \(f'(x)\) , giving your answer in the form \(a{\sin ^p}x{\cos ^q}x\) where \(a{\text{, }}p{\text{, }}q \in \mathbb{Z}\) .
Let \(g(x) = \sqrt 3 \sin x{(\cos x)^{\frac{1}{2}}}\) for \(0 \le x \le \frac{\pi }{2}\) . Find the volume generated when the curve of g is revolved through \(2\pi \) about the x-axis.
Answer/Explanation
Markscheme
(i) range of f is \([ – 1{\text{, }}1]\) , \(( – 1 \le f(x) \le 1)\) A2 N2
(ii) \({\sin ^3}x \Rightarrow 1 \Rightarrow \sin x = 1\) A1
justification for one solution on \([0{\text{, }}2\pi ]\) R1
e.g. \(x = \frac{\pi }{2}\) , unit circle, sketch of \(\sin x\)
1 solution (seen anywhere) A1 N1
[5 marks]
\(f'(x) = 3{\sin ^2}x\cos x\) A2 N2
[2 marks]
using \(V = \int_a^b {\pi {y^2}{\rm{d}}x} \) (M1)
\(V = \int_0^{\frac{\pi }{2}} {\pi (\sqrt 3 } \sin x{\cos ^{\frac{1}{2}}}x{)^2}{\rm{d}}x\) (A1)
\( = \pi \int_0^{\frac{\pi }{2}} {3{{\sin }^2}x\cos x{\rm{d}}x} \) A1
\(V = \pi \left[ {{{\sin }^3}x} \right]_0^{\frac{\pi }{2}}\) \(\left( { = \pi \left( {{{\sin }^3}\left( {\frac{\pi }{2}} \right) – {{\sin }^3}0} \right)} \right)\) A2
evidence of using \(\sin \frac{\pi }{2} = 1\) and \(\sin 0 = 0\) (A1)
e.g. \(\pi \left( {1 – 0} \right)\)
\(V = \pi \) A1 N1
[7 marks]
Question
Let \(f(x) = {{\rm{e}}^{ – 3x}}\) and \(g(x) = \sin \left( {x – \frac{\pi }{3}} \right)\) .
Write down
(i) \(f'(x)\) ;
(ii) \(g'(x)\) .
Let \(h(x) = {{\rm{e}}^{ – 3x}}\sin \left( {x – \frac{\pi }{3}} \right)\) . Find the exact value of \(h’\left( {\frac{\pi }{3}} \right)\) .
Answer/Explanation
Markscheme
(i) \( – 3{{\rm{e}}^{ – 3x}}\) A1 N1
(ii) \(\cos \left( {x – \frac{\pi }{3}} \right)\) A1 N1
[4 marks]
evidence of choosing product rule (M1)
e.g. \(uv’ + vu’\)
correct expression A1
e.g. \( – 3{{\rm{e}}^{ – 3x}}\sin \left( {x – \frac{\pi }{3}} \right) + {{\rm{e}}^{ – 3x}}\cos \left( {x – \frac{\pi }{3}} \right)\)
complete correct substitution of \(x = \frac{\pi }{3}\) (A1)
e.g. \( – 3{{\rm{e}}^{ – 3\frac{\pi }{3}}}\sin \left( {\frac{\pi }{3} – \frac{\pi }{3}} \right) + {{\rm{e}}^{ – 3\frac{\pi }{3}}}\cos \left( {\frac{\pi }{3} – \frac{\pi }{3}} \right)\)
\(h’\left( {\frac{\pi }{3}} \right) = {{\rm{e}}^{ – \pi }}\) A1 N3
[4 marks]
Question
Let \(g(x) = 2x\sin x\) .
Find \(g'(x)\) .
Find the gradient of the graph of g at \(x = \pi \) .
Answer/Explanation
Markscheme
evidence of choosing the product rule (M1)
e.g. \(uv’ + vu’\)
correct derivatives \(\cos x\) , 2 (A1)(A1)
\(g'(x) = 2x\cos x + 2\sin x\) A1 N4
[4 marks]
attempt to substitute into gradient function (M1)
e.g. \(g'(\pi )\)
correct substitution (A1)
e.g. \(2\pi \cos \pi + 2\sin \pi \)
\({\text{gradient}} = – 2\pi \) A1 N2
[3 marks]
Question
Consider f(x), g(x) and h(x), for x∈\(\mathbb{R}\) where h(x) = \(\left( {f \circ g} \right)\)(x).
Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.
Answer/Explanation
Markscheme
recognizing the need to find h′ (M1)
recognizing the need to find h′ (3) (seen anywhere) (M1)
evidence of choosing chain rule (M1)
eg \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{\text{d}}y}}{{{\text{d}}u}} \times \frac{{{\text{d}}u}}{{{\text{d}}x}},\,\,f’\left( {g\left( 3 \right)} \right) \times g’\left( 3 \right),\,\,f’\left( g \right) \times g’\)
correct working (A1)
eg \(f’\left( 7 \right) \times 4,\,\, – 5 \times 4\)
\(h’\left( 3 \right) = – 20\) (A1)
evidence of taking their negative reciprocal for normal (M1)
eg \( – \frac{1}{{h’\left( 3 \right)}},\,\,{m_1}{m_2} = – 1\)
gradient of normal is \(\frac{1}{{20}}\) A1 N4
[7 marks]
Question
Find the derivative of each function below.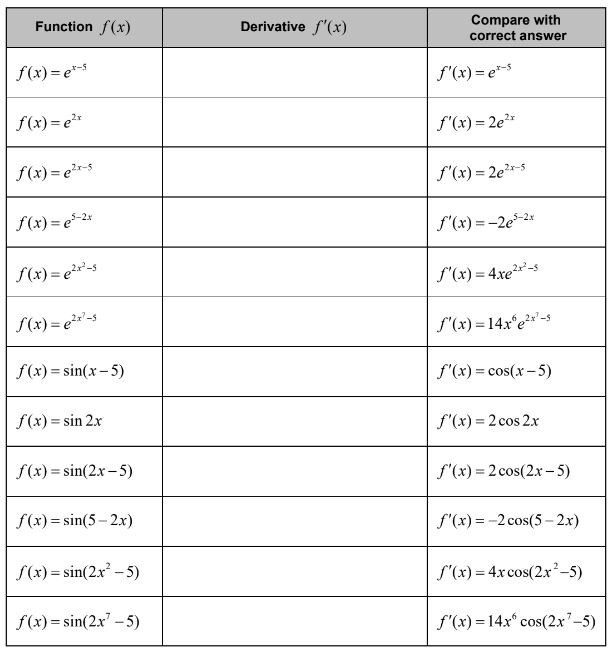



Answer/Explanation
Ans:
Solutions are shown in the question.