Question
A function f has its first derivative given by \(f'(x) = {(x – 3)^3}\) .
Find the second derivative.
Find \(f'(3)\) and \(f”(3)\) .
The point P on the graph of f has x-coordinate \(3\). Explain why P is not a point of inflexion.
Answer/Explanation
Markscheme
METHOD 1
\(f”(x) = 3{(x – 3)^2}\) A2 N2
METHOD 2
attempt to expand \({(x – 3)^3}\) (M1)
e.g. \(f'(x) = {x^3} – 9{x^2} + 27x – 27\)
\(f”(x) = 3{x^2} – 18x + 27\) A1 N2
[2 marks]
\(f'(3) = 0\) , \(f”(3) = 0\) A1 N1
[1 mark]
METHOD 1
\({f”}\) does not change sign at P R1
evidence for this R1 N0
METHOD 2
\({f’}\) changes sign at P so P is a maximum/minimum (i.e. not inflexion) R1
evidence for this R1 N0
METHOD 3
finding \(f(x) = \frac{1}{4}{(x – 3)^4} + c\) and sketching this function R1
indicating minimum at \(x = 3\) R1 N0
[2 marks]
Question
Let \(f(x) = \frac{{\cos x}}{{\sin x}}\) , for \(\sin x \ne 0\) .
In the following table, \(f’\left( {\frac{\pi }{2}} \right) = p\) and \(f”\left( {\frac{\pi }{2}} \right) = q\) . The table also gives approximate values of \(f'(x)\) and \(f”(x)\) near \(x = \frac{\pi }{2}\) .
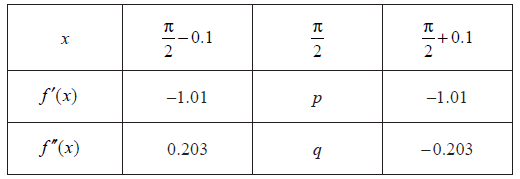
Use the quotient rule to show that \(f'(x) = \frac{{ – 1}}{{{{\sin }^2}x}}\) .
Find \(f”(x)\) .
Find the value of p and of q.
Use information from the table to explain why there is a point of inflexion on the graph of f where \(x = \frac{\pi }{2}\) .
Answer/Explanation
Markscheme
\(\frac{{\rm{d}}}{{{\rm{d}}x}}\sin x = \cos x\) , \(\frac{{\rm{d}}}{{{\rm{d}}x}}\cos x = – \sin x\) (seen anywhere) (A1)(A1)
evidence of using the quotient rule M1
correct substitution A1
e.g. \(\frac{{\sin x( – \sin x) – \cos x(\cos x)}}{{{{\sin }^2}x}}\) , \(\frac{{ – {{\sin }^2}x – {{\cos }^2}x}}{{{{\sin }^2}x}}\)
\(f'(x) = \frac{{ – ({{\sin }^2}x + {{\cos }^2}x)}}{{{{\sin }^2}x}}\) A1
\(f'(x) = \frac{{ – 1}}{{{{\sin }^2}x}}\) AG N0
[5 marks]
METHOD 1
appropriate approach (M1)
e.g. \(f'(x) = – {(\sin x)^{ – 2}}\)
\(f”(x) = 2({\sin ^{ – 3}}x)(\cos x)\) \(\left( { = \frac{{2\cos x}}{{{{\sin }^3}x}}} \right)\) A1A1 N3
Note: Award A1 for \(2{\sin ^{ – 3}}x\) , A1 for \(\cos x\) .
METHOD 2
derivative of \({\sin ^2}x = 2\sin x\cos x\) (seen anywhere) A1
evidence of choosing quotient rule (M1)
e.g. \(u = – 1\) , \(v = {\sin ^2}x\) , \(f” = \frac{{{{\sin }^2}x \times 0 – ( – 1)2\sin x\cos x}}{{{{({{\sin }^2}x)}^2}}}\)
\(f”(x) = \frac{{2\sin x\cos x}}{{{{({{\sin }^2}x)}^2}}}\) \(\left( { = \frac{{2\cos x}}{{{{\sin }^3}x}}} \right)\) A1 N3
[3 marks]
evidence of substituting \(\frac{\pi }{2}\) M1
e.g. \(\frac{{ – 1}}{{{{\sin }^2}\frac{\pi }{2}}}\) , \(\frac{{2\cos \frac{\pi }{2}}}{{{{\sin }^3}\frac{\pi }{2}}}\)
\(p = – 1\) , \(q = 0\) A1A1 N1N1
[3 marks]
second derivative is zero, second derivative changes sign R1R1 N2
[2 marks]
Question
A function f (x) has derivative f ′(x) = 3x2 + 18x. The graph of f has an x-intercept at x = −1.
Find f (x).
The graph of f has a point of inflexion at x = p. Find p.
Find the values of x for which the graph of f is concave-down.
Answer/Explanation
Markscheme
evidence of integration (M1)
eg \(\int {f’\left( x \right)} \)
correct integration (accept absence of C) (A1)(A1)
eg \({x^3} + \frac{{18}}{2}{x^2} + C,\,\,{x^3} + 9{x^2}\)
attempt to substitute x = −1 into their f = 0 (must have C) M1
eg \({\left( { – 1} \right)^3} + 9{\left( { – 1} \right)^2} + C = 0,\,\, – 1 + 9 + C = 0\)
Note: Award M0 if they substitute into original or differentiated function.
correct working (A1)
eg \(8 + C = 0,\,\,\,C = – 8\)
\(f\left( x \right) = {x^3} + 9{x^2} – 8\) A1 N5
[6 marks]
METHOD 1 (using 2nd derivative)
recognizing that f” = 0 (seen anywhere) M1
correct expression for f” (A1)
eg 6x + 18, 6p + 18
correct working (A1)
6p + 18 = 0
p = −3 A1 N3
METHOD 1 (using 1st derivative)
recognizing the vertex of f′ is needed (M2)
eg \( – \frac{b}{{2a}}\) (must be clear this is for f′)
correct substitution (A1)
eg \(\frac{{ – 18}}{{2 \times 3}}\)
p = −3 A1 N3
[4 marks]
valid attempt to use f” (x) to determine concavity (M1)
eg f” (x) < 0, f” (−2), f” (−4), 6x + 18 ≤ 0
correct working (A1)
eg 6x + 18 < 0, f” (−2) = 6, f” (−4) = −6
f concave down for x < −3 (do not accept x ≤ −3) A1 N2
[3 marks]