Question
The function h is defined by h(x) = \(2xe^x\) + 3, for \(x \epsilon \mathbb{R}\). The following diagram shows part of the graph of h, which has a local minimum at point A.
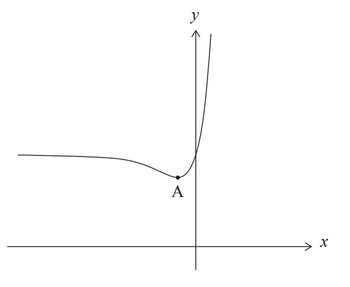
(a) Find the value of the y-intercept.
(b) Find h′(x).
(c) Hence, find the coordinates of A.
(d) (i) Show that h′′(x) = (2x + 4)\(e^x\).
(ii) Find the values of x for which the graph of h is concave-up.
Answer/Explanation
Answer:
(a) substitution of x = 0
(y = 3) (accept (0, 3 ))
(b) evidence of using the product rule
h'(x) = 2\(e^x\) + 2x\(e^x\)
(c) setting their derivative equal to zero
correct working
\(2e^x\) (1 + x) (=0) OR -2x = 2
x = -1 (seen anywhere, and must follow on from their derivative)
substituting their value of x into h(x)
\(y = -\frac{2}{e} +3\) (= – 2\(e^{-1} + 3\))
A(-1, – \(\frac{2}{e}\) + 3)
(d) (i) h”(x) = \(2e^x + 2e^x + 2xe^x\) OR \(2e^x + 2e^x (1 + x)\)
h”(x) = (2x + 4)\(e^x\)
(ii) recognition that h”>0 OR attempt to find point of inflexion
since \(e^x\) > 0, 2x + 4 > 0 OR 2x + 4 = 0 (⇒ x = -2)
x > -2
Question
Consider \(f(x) = \frac{1}{3}{x^3} + 2{x^2} – 5x\) . Part of the graph of f is shown below. There is a maximum point at M, and a point of inflexion at N.
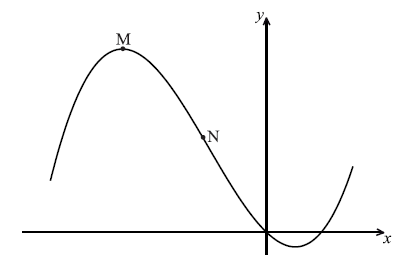
Find \(f'(x)\) .
Find the x-coordinate of M.
Find the x-coordinate of N.
The line L is the tangent to the curve of f at \((3{\text{, }}12)\). Find the equation of L in the form \(y = ax + b\) .
Answer/Explanation
Markscheme
\(f'(x) = {x^2} + 4x – 5\) A1A1A1 N3
[3 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
evidence of correct working A1
e.g. \((x + 5)(x – 1)\) , \(\frac{{ – 4 \pm \sqrt {16 + 20} }}{2}\) , sketch
\(x = – 5\), \(x = 1\) (A1)
so \(x = – 5\) A1 N2
[4 marks]
METHOD 1
\(f”(x) = 2x + 4\) (may be seen later) A1
evidence of setting second derivative = 0 (M1)
e.g. \(2x + 4 = 0\)
\(x = – 2\) A1 N2
METHOD 2
evidence of use of symmetry (M1)
e.g. midpoint of max/min, reference to shape of cubic
correct calculation A1
e.g. \(\frac{{ – 5 + 1}}{2}\)
\(x = – 2\) A1 N2
[3 marks]
attempting to find the value of the derivative when \(x = 3\) (M1)
\(f'(3) = 16\) A1
valid approach to finding the equation of a line M1
e.g. \(y – 12 = 16(x – 3)\) , \(12 = 16 \times 3 + b\)
\(y = 16x – 36\) A1 N2
[4 marks]
Question
The diagram shows part of the graph of \(y = f'(x)\) . The x-intercepts are at points A and C. There is a minimum at B, and a maximum at D.
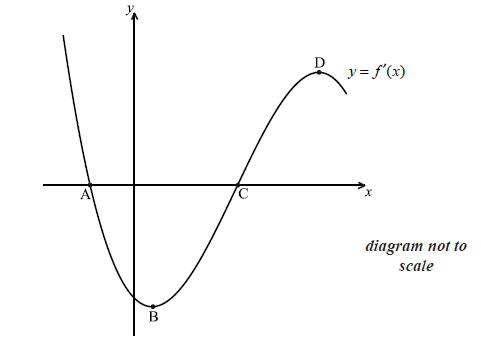
(i) Write down the value of \(f'(x)\) at C.
(ii) Hence, show that C corresponds to a minimum on the graph of f , i.e. it has the same x-coordinate.
Which of the points A, B, D corresponds to a maximum on the graph of f ?
Show that B corresponds to a point of inflexion on the graph of f .
Answer/Explanation
Markscheme
(i) \(f'(x) = 0\) A1 N1
(ii) METHOD 1
\(f'(x) < 0\) to the left of C, \(f'(x) > 0\) to the right of C R1R1 N2
METHOD 2
\(f”(x) > 0\) R2 N2
[3 marks]
A A1 N1
[1 mark]
METHOD 1
\(f”(x) = 0\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
METHOD 2
B is a minimum on the graph of the derivative \({f’}\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
[3 marks]
Question
The diagram shows part of the graph of \(y = f'(x)\) . The x-intercepts are at points A and C. There is a minimum at B, and a maximum at D.

(i) Write down the value of \(f'(x)\) at C.
(ii) Hence, show that C corresponds to a minimum on the graph of f , i.e. it has the same x-coordinate.
Which of the points A, B, D corresponds to a maximum on the graph of f ?
Show that B corresponds to a point of inflexion on the graph of f .
Answer/Explanation
Markscheme
(i) \(f'(x) = 0\) A1 N1
(ii) METHOD 1
\(f'(x) < 0\) to the left of C, \(f'(x) > 0\) to the right of C R1R1 N2
METHOD 2
\(f”(x) > 0\) R2 N2
[3 marks]
A A1 N1
[1 mark]
METHOD 1
\(f”(x) = 0\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
METHOD 2
B is a minimum on the graph of the derivative \({f’}\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
[3 marks]