Question
The following diagram shows a semicircle centre O, diameter [AB], with radius 2.
Let P be a point on the circumference, with \({\rm{P}}\widehat {\rm{O}}{\rm{B}} = \theta \) radians.
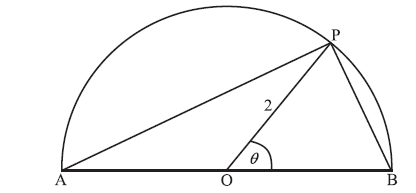
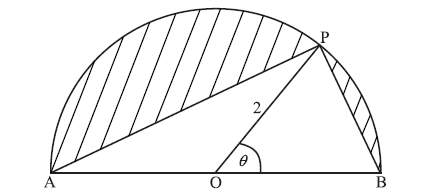
Let S be the total area of the two segments shaded in the diagram below.
Find the area of the triangle OPB, in terms of \(\theta \) .
Explain why the area of triangle OPA is the same as the area triangle OPB.
Show that \(S = 2(\pi – 2\sin \theta )\) .
Find the value of \(\theta \) when S is a local minimum, justifying that it is a minimum.
Find a value of \(\theta \) for which S has its greatest value.
Answer/Explanation
Markscheme
evidence of using area of a triangle (M1)
e.g. \(A = \frac{1}{2} \times 2 \times 2 \times \sin \theta \)
\(A = 2\sin \theta \) A1 N2
[2 marks]
METHOD 1
\({\rm{P}}\widehat {\rm{O}}{\rm{A = }}\pi – \theta \) (A1)
\({\text{area }}\Delta {\rm{OPA}} = \frac{1}{2}2 \times 2 \times \sin (\pi – \theta )\) \(( = 2\sin (\pi – \theta ))\) A1
since \(\sin (\pi – \theta ) = \sin \theta \) R1
then both triangles have the same area AG N0
METHOD 2
triangle OPA has the same height and the same base as triangle OPB R3
then both triangles have the same area AG N0
[3 marks]
area semicircle \( = \frac{1}{2} \times \pi {(2)^2}\) \(( = 2\pi )\) A1
\({\text{area }}\Delta {\rm{APB}} = 2\sin \theta + 2\sin \theta \) \(( = 4\sin \theta )\) A1
\(S{\text{ = area of semicircle}} – {\text{area }}\Delta {\rm{APB}}\) \(( = 2\pi – 4\sin \theta )\) M1
\(S = 2(\pi – 2\sin \theta )\) AG N0
[3 marks]
METHOD 1
attempt to differentiate (M1)
e.g. \(\frac{{{\rm{d}}S}}{{{\rm{d}}\theta }} = – 4\cos \theta \)
setting derivative equal to 0 (M1)
correct equation A1
e.g. \( – 4\cos \theta = 0\) , \(\cos \theta = 0\) , \(4\cos \theta = 0\)
\(\theta = \frac{\pi }{2}\) A1 N3
EITHER
evidence of using second derivative (M1)
\(S”(\theta ) = 4\sin \theta \) A1
\(S”\left( {\frac{\pi }{2}} \right) = 4\) A1
it is a minimum because \(S”\left( {\frac{\pi }{2}} \right) > 0\) R1 N0
OR
evidence of using first derivative (M1)
for \(\theta < \frac{\pi }{2},S'(\theta ) < 0\) (may use diagram) A1
for \(\theta > \frac{\pi }{2},S'(\theta ) > 0\) (may use diagram) A1
it is a minimum since the derivative goes from negative to positive R1 N0
METHOD 2
\(2\pi – 4\sin \theta \) is minimum when \(4\sin \theta \) is a maximum R3
\(4\sin \theta \) is a maximum when \(\sin \theta = 1\) (A2)
\(\theta = \frac{\pi }{2}\) A3 N3
[8 marks]
S is greatest when \(4\sin \theta \) is smallest (or equivalent) (R1)
\(\theta = 0\) (or \(\pi \) ) A1 N2
[2 marks]
Question
Fred makes an open metal container in the shape of a cuboid, as shown in the following diagram.
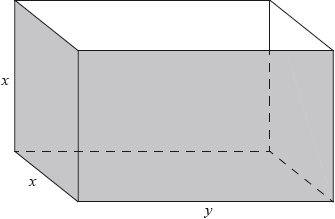
The container has height \(x{\text{ m}}\), width \(x{\text{ m}}\) and length \(y{\text{ m}}\). The volume is \(36{\text{ }}{{\text{m}}^3}\).
Let \(A(x)\) be the outside surface area of the container.
Show that \(A(x) = \frac{{108}}{x} + 2{x^2}\).
Find \(A'(x)\).
Given that the outside surface area is a minimum, find the height of the container.
Fred paints the outside of the container. A tin of paint covers a surface area of \({\text{10 }}{{\text{m}}^{\text{2}}}\) and costs $20. Find the total cost of the tins needed to paint the container.
Answer/Explanation
Markscheme
correct substitution into the formula for volume A1
eg\(\,\,\,\,\,\)\(36 = y \times x \times x\)
valid approach to eliminate \(y\) (may be seen in formula/substitution) M1
eg\(\,\,\,\,\,\)\(y = \frac{{36}}{{{x^2}}},{\text{ }}xy = \frac{{36}}{x}\)
correct expression for surface area A1
eg\(\,\,\,\,\,\)\(xy + xy + xy + {x^2} + {x^2},{\text{ area}} = 3xy + 2{x^2}\)
correct expression in terms of \(x\) only A1
eg\(\,\,\,\,\,\)\(3x\left( {\frac{{36}}{{{x^2}}}} \right) + 2{x^2},{\text{ }}{x^2} + {x^2} + \frac{{36}}{x} + \frac{{36}}{x} + \frac{{36}}{x},{\text{ }}2{x^2} + 3\left( {\frac{{36}}{x}} \right)\)
\(A(x) = \frac{{108}}{x} + 2{x^2}\) AG N0
[4 marks]
\(A'(x) = – \frac{{108}}{{{x^2}}} + 4x,{\text{ }}4x – 108{x^{ – 2}}\) A1A1 N2
Note: Award A1 for each term.
[2 marks]
recognizing that minimum is when \(A'(x) = 0\) (M1)
correct equation (A1)
eg\(\,\,\,\,\,\)\( – \frac{{108}}{{{x^2}}} + 4x = 0,{\text{ }}4x = \frac{{108}}{{{x^2}}}\)
correct simplification (A1)
eg\(\,\,\,\,\,\)\( – 108 + 4{x^3} = 0,{\text{ }}4{x^3} = 108\)
correct working (A1)
eg\(\,\,\,\,\,\)\({x^3} = 27\)
\({\text{height}} = 3{\text{ (m) }}({\text{accept }}x = 3)\) A1 N2
[5 marks]
attempt to find area using their height (M1)
eg\(\,\,\,\,\,\)\(\frac{{108}}{3} + 2{(3)^2},{\text{ }}9 + 9 + 12 + 12 + 12\)
minimum surface area \( = 54{\text{ }}{{\text{m}}^{\text{2}}}\) (may be seen in part (c)) A1
attempt to find the number of tins (M1)
eg\(\,\,\,\,\,\)\(\frac{{54}}{{10}},{\text{ }}5.4\)
6 (tins) (A1)
$120 A1 N3
[5 marks]
Question
A rectangle has sides x and y and its perimeter is 40m.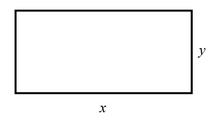
(a) Express y in term of x.
(b) Hence, express the area A of the rectangle in terms of x.
(c) Use \(\frac{dA}{dx}\) to find the maximum area of the rectangle, justify your answer.
(d) What is the minimum value of A?
Answer/Explanation
Ans:
(a) \(2x+2y=40 \Leftrightarrow x+y = 20 \Leftrightarrow y = 20 – x\)
(b) \(A=x(20-x)=20x-x^2\)
(c) \(\frac{dA}{dx}=20-2x\)
\(20-2x=0 \Leftrightarrow x = 10\)
\(\frac{d^2A}{dx^2}=-2<0\) so x = 10 gives a maximum.
It is a square of side x = 10 and the maximum area is A = 100
(d) The domain of A = x(20-x) is \(0 \leq x \leq 20\). At the endpoints x = 0 and x = 20, the area A = 0