Question
A farmer wishes to create a rectangular enclosure, ABCD, of area 525 m2, as shown below.

The fencing used for side AB costs \(\$ 11\) per metre. The fencing for the other three sides costs \(\$ 3\) per metre. The farmer creates an enclosure so that the cost is a minimum. Find this minimum cost.
Answer/Explanation
Markscheme
METHOD 1
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AB}} = x\) , \({\rm{AD}} = \frac{{525}}{x}\)
attempt to set up cost function using $3 for three sides and $11 for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(\frac{{525}}{x} \times 3 + \frac{{525}}{x} \times 3 + 11x + 3x\) , \(\frac{{525}}{{{\rm{AB}}}} \times 3 + \frac{{525}}{{{\rm{AB}}}} \times 3 + 11{\rm{AB}} + 3{\rm{AB}}\) , \(\frac{{3150}}{x} + 14x\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 15\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = \frac{{ – 1575}}{{{x^2}}} + \frac{{ – 1575}}{{{x^2}}} + 14\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(\frac{{ – 3150}}{{{x^2}}} + 14 = 0\)
minimum cost is 420 (dollars) A1 N4
METHOD 2
correct expression for second side, using area = 525 (A1)
e.g. let \({\rm{AD}} = x\) , \({\rm{AB}} = \frac{{525}}{x}\)
attempt to set up cost function using \(\$ 3\) for three sides and \(\$ 11\) for one side (M1)
e.g. \(3({\rm{AD}} + {\rm{BC}} + {\rm{CD}}) + 11{\rm{AB}}\)
correct expression for cost A2
e.g. \(3\left( {x + x + \frac{{525}}{x}} \right) + \frac{{525}}{x} \times 11\) , \(3\left( {{\rm{AD}} + {\rm{AD}} + \frac{{525}}{{{\rm{AD}}}}} \right) + \frac{{525}}{{{\rm{AD}}}} \times 11\) , \(6x + \frac{{7350}}{x}\)
EITHER
sketch of cost function (M1)
identifying minimum point (A1)
e.g. marking point on graph, \(x = 35\)
minimum cost is 420 (dollars) A1 N4
OR
correct derivative (may be seen in equation below) (A1)
e.g. \(C'(x) = 6 – \frac{{7350}}{{{x^2}}}\)
setting their derivative equal to 0 (seen anywhere) (M1)
e.g. \(6 – \frac{{7350}}{{{x^2}}} = 0\)
minimum cost is 420 (dollars) A1 N4
[7 marks]
Question
The diagram below shows a plan for a window in the shape of a trapezium.
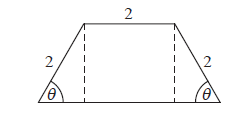
Three sides of the window are \(2{\text{ m}}\) long. The angle between the sloping sides of the window and the base is \(\theta \) , where \(0 < \theta < \frac{\pi }{2}\) .
Show that the area of the window is given by \(y = 4\sin \theta + 2\sin 2\theta \) .
Zoe wants a window to have an area of \(5{\text{ }}{{\text{m}}^2}\). Find the two possible values of \(\theta \) .
John wants two windows which have the same area A but different values of \(\theta \) .
Find all possible values for A .
Answer/Explanation
Markscheme
evidence of finding height, h (A1)
e.g. \(\sin \theta = \frac{h}{2}\) , \(2\sin \theta \)
evidence of finding base of triangle, b (A1)
e.g. \(\cos \theta = \frac{b}{2}\) , \(2\cos \theta \)
attempt to substitute valid values into a formula for the area of the window (M1)
e.g. two triangles plus rectangle, trapezium area formula
correct expression (must be in terms of \(\theta \) ) A1
e.g. \(2\left( {\frac{1}{2} \times 2\cos \theta \times 2\sin \theta } \right) + 2 \times 2\sin \theta \) , \(\frac{1}{2}(2\sin \theta )(2 + 2 + 4\cos \theta )\)
attempt to replace \(2\sin \theta \cos \theta \) by \(\sin 2\theta \) M1
e.g. \(4\sin \theta + 2(2\sin \theta \cos \theta )\)
\(y = 4\sin \theta + 2\sin 2\theta \) AG N0
[5 marks]
correct equation A1
e.g. \(y = 5\) , \(4\sin \theta + 2\sin 2\theta = 5\)
evidence of attempt to solve (M1)
e.g. a sketch, \(4\sin \theta + 2\sin \theta – 5 = 0\)
\(\theta = 0.856\) \(({49.0^ \circ })\) , \(\theta = 1.25\) \(({71.4^ \circ })\) A1A1 N3
[4 marks]
recognition that lower area value occurs at \(\theta = \frac{\pi }{2}\) (M1)
finding value of area at \(\theta = \frac{\pi }{2}\) (M1)
e.g. \(4\sin \left( {\frac{\pi }{2}} \right) + 2\sin \left( {2 \times \frac{\pi }{2}} \right)\) , draw square
\(A = 4\) (A1)
recognition that maximum value of y is needed (M1)
\(A = 5.19615 \ldots \) (A1)
\(4 < A < 5.20\) (accept \(4 < A < 5.19\) ) A2 N5
[7 marks]
Question
Let \(f(x) = \frac{{100}}{{(1 + 50{{\rm{e}}^{ – 0.2x}})}}\) . Part of the graph of \(f\) is shown below.
Write down \(f(0)\) .
Solve \(f(x) = 95\) .
Find the range of \(f\) .
Show that \(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) .
Find the maximum rate of change of \(f\) .
Answer/Explanation
Markscheme
\(f(0) = \frac{{100}}{{51}}\) (exact), \(1.96\) A1 N1
[1 mark]
setting up equation (M1)
eg \(95 = \frac{{100}}{{1 + 50{{\rm{e}}^{ – 0.2x}}}}\) , sketch of graph with horizontal line at \(y = 95\)
\(x = 34.3\) A1 N2
[2 marks]
upper bound of \(y\) is \(100\) (A1)
lower bound of \(y\) is \(0\) (A1)
range is \(0 < y < 100\) A1 N3
[3 marks]
METHOD 1
setting function ready to apply the chain rule (M1)
eg \(100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 1}}\)
evidence of correct differentiation (must be substituted into chain rule) (A1)(A1)
eg \(u’ = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\) , \(v’ = (50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct chain rule derivative A1
eg \(f'(x) = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}(50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct working clearly leading to the required answer A1
eg \(f'(x) = 1000{{\rm{e}}^{ – 0.2x}}{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\)
\(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
METHOD 2
attempt to apply the quotient rule (accept reversed numerator terms) (M1)
eg \(\frac{{vu’ – uv’}}{{{v^2}}}\) , \(\frac{{uv’ – vu’}}{{{v^2}}}\)
evidence of correct differentiation inside the quotient rule (A1)(A1)
eg \(f'(x) = \frac{{(1 + 50{{\rm{e}}^{ – 0.2x}})(0) – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{100( – 10){{\rm{e}}^{ – 0.2x}} – 0}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
any correct expression for derivative (\(0\) may not be explicitly seen) (A1)
eg \(\frac{{ – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
correct working clearly leading to the required answer A1
eg \(f'(x) = \frac{{0 – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{ – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
\(f'(x) = \frac{{{\rm{1000}}{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
[5 marks]
METHOD 1
sketch of \(f'(x)\) (A1)
eg
recognizing maximum on \(f'(x)\) (M1)
eg dot on max of sketch
finding maximum on graph of \(f'(x)\) A1
eg (\(19.6\), \(5\)) , \(x = 19.560 \ldots \)
maximum rate of increase is \(5\) A1 N2
METHOD 2
recognizing \(f”(x) = 0\) (M1)
finding any correct expression for \(f”(x) = 0\) (A1)
eg \(\frac{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}( – 200{{\rm{e}}^{ – 0.2x}}) – (1000{{\rm{e}}^{ – 0.2x}})(2(1 + 50{{\rm{e}}^{ – 0.2x}})( – 10{{\rm{e}}^{ – 0.2x}}))}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^4}}}\)
finding \(x = 19.560 \ldots \) A1
maximum rate of increase is \(5\) A1 N2
[4 marks]
Question
Let \(f(x) = \frac{{3x}}{{x – q}}\), where \(x \ne q\).
Write down the equations of the vertical and horizontal asymptotes of the graph of \(f\).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
Find the value of \(q\).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
The point \({\text{P}}(x,{\text{ }}y)\) lies on the graph of \(f\). Show that \({\text{PQ}} = \sqrt {{{(x – 1)}^2} + {{\left( {\frac{3}{{x – 1}}} \right)}^2}} \).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
Hence find the coordinates of the points on the graph of \(f\) that are closest to \((1,3)\).
Answer/Explanation
Markscheme
\(x = q,{\text{ }}y = 3\) (must be equations) A1A1 N2
[2 marks]
recognizing connection between point of intersection and asymptote (R1)
eg \(x = 1\)
\(q = 1\) A1 N2
[2 marks]
correct substitution into distance formula A1
eg \(\sqrt {{{(x – 1)}^2} + {{(y – 3)}^2}} \)
attempt to substitute \(y = \frac{{3x}}{{x – 1}}\) (M1)
eg \(\sqrt {{{(x – 1)}^2} + {{\left( {\frac{{3x}}{{x – 1}} – 3} \right)}^2}} \)
correct simplification of \(\left( {\frac{{3x}}{{x – 1}} – 3} \right)\) (A1)
eg \(\frac{{3x – 3x(x – 1)}}{{x – 1}}\)
correct expression clearly leading to the required answer A1
eg \(\frac{{3x – 3x + 3}}{{x – 1}},{\text{ }}\sqrt {{{(x – 1)}^2} + {{\left( {\frac{{3x – 3x + 3}}{{x – 1}}} \right)}^2}} \)
\({\text{PQ}} = \sqrt {{{(x – 1)}^2} + {{\left( {\frac{3}{{x – 1}}} \right)}^2}} \) AG N0
[4 marks]
recognizing that closest is when \({\text{PQ}}\) is a minimum (R1)
eg sketch of \({\text{PQ}}\), \(({\text{PQ}})'(x) = 0\)
\(x = – 0.73205{\text{ }}x = 2.73205\) (seen anywhere) A1A1
attempt to find y-coordinates (M1)
eg \(f( – 0.73205)\)
\((-0.73205, 1.267949) , (2.73205, 4.73205)\)
\((-0.732, 1.27) , (2.73, 4.73) \) A1A1 N4
[6 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
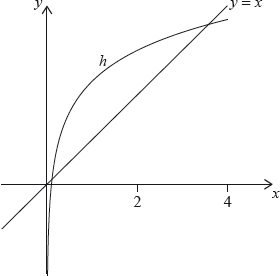
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]
