Question
The diagram shows part of the graph of \(y = f'(x)\) . The x-intercepts are at points A and C. There is a minimum at B, and a maximum at D.
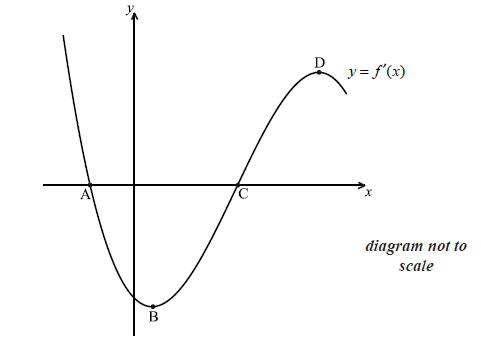
(i) Write down the value of \(f'(x)\) at C.
(ii) Hence, show that C corresponds to a minimum on the graph of f , i.e. it has the same x-coordinate.
Which of the points A, B, D corresponds to a maximum on the graph of f ?
Show that B corresponds to a point of inflexion on the graph of f .
Answer/Explanation
Markscheme
(i) \(f'(x) = 0\) A1 N1
(ii) METHOD 1
\(f'(x) < 0\) to the left of C, \(f'(x) > 0\) to the right of C R1R1 N2
METHOD 2
\(f”(x) > 0\) R2 N2
[3 marks]
A A1 N1
[1 mark]
METHOD 1
\(f”(x) = 0\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
METHOD 2
B is a minimum on the graph of the derivative \({f’}\) R2
discussion of sign change of \(f”(x)\) R1
e.g. \(f”(x) < 0\) to the left of B and \(f”(x) > 0\) to the right of B; \(f”(x)\) changes sign either side of B
B is a point of inflexion AG N0
[3 marks]
Question
A function f has its first derivative given by \(f'(x) = {(x – 3)^3}\) .
Find the second derivative.
Find \(f'(3)\) and \(f”(3)\) .
The point P on the graph of f has x-coordinate \(3\). Explain why P is not a point of inflexion.
Answer/Explanation
Markscheme
METHOD 1
\(f”(x) = 3{(x – 3)^2}\) A2 N2
METHOD 2
attempt to expand \({(x – 3)^3}\) (M1)
e.g. \(f'(x) = {x^3} – 9{x^2} + 27x – 27\)
\(f”(x) = 3{x^2} – 18x + 27\) A1 N2
[2 marks]
\(f'(3) = 0\) , \(f”(3) = 0\) A1 N1
[1 mark]
METHOD 1
\({f”}\) does not change sign at P R1
evidence for this R1 N0
METHOD 2
\({f’}\) changes sign at P so P is a maximum/minimum (i.e. not inflexion) R1
evidence for this R1 N0
METHOD 3
finding \(f(x) = \frac{1}{4}{(x – 3)^4} + c\) and sketching this function R1
indicating minimum at \(x = 3\) R1 N0
[2 marks]