Question
Let \(f(x) = 6 + 6\sin x\) . Part of the graph of f is shown below.
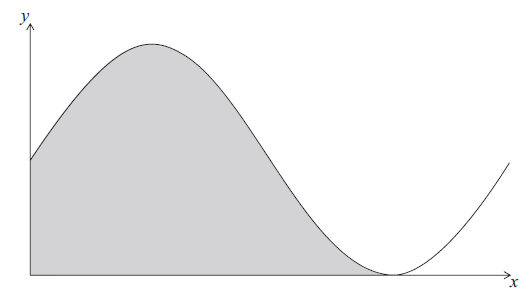
The shaded region is enclosed by the curve of f , the x-axis, and the y-axis.
Solve for \(0 \le x < 2\pi \)
(i) \(6 + 6\sin x = 6\) ;
(ii) \(6 + 6\sin x = 0\) .
Write down the exact value of the x-intercept of f , for \(0 \le x < 2\pi \) .
The area of the shaded region is k . Find the value of k , giving your answer in terms of \(\pi \) .
Let \(g(x) = 6 + 6\sin \left( {x – \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Give a full geometric description of this transformation.
Let \(g(x) = 6 + 6\sin \left( {x – \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Given that \(\int_p^{p + \frac{{3\pi }}{2}} {g(x){\rm{d}}x} = k\) and \(0 \le p < 2\pi \) , write down the two values of p.
Answer/Explanation
Markscheme
(i) \(\sin x = 0\) A1
\(x = 0\) , \(x = \pi \) A1A1 N2
(ii) \(\sin x = – 1\) A1
\(x = \frac{{3\pi }}{2}\) A1 N1
[5 marks]
\(\frac{{3\pi }}{2}\) A1 N1
[1 mark]
evidence of using anti-differentiation (M1)
e.g. \(\int_0^{\frac{{3\pi }}{2}} {(6 + 6\sin x){\rm{d}}x} \)
correct integral \(6x – 6\cos x\) (seen anywhere) A1A1
correct substitution (A1)
e.g. \(6\left( {\frac{{3\pi }}{2}} \right) – 6\cos \left( {\frac{{3\pi }}{2}} \right) – ( – 6\cos 0)\) , \(9\pi – 0 + 6\)
\(k = 9\pi + 6\) A1A1 N3
[6 marks]
translation of \(\left( {\begin{array}{*{20}{c}}
{\frac{\pi }{2}}\\
0
\end{array}} \right)\) A1A1 N2
[2 marks]
recognizing that the area under g is the same as the shaded region in f (M1)
\(p = \frac{\pi }{2}\) , \(p = 0\) A1A1 N3
[3 marks]
Question
The following diagram shows part of the graph of the function \(f(x) = 2{x^2}\) .
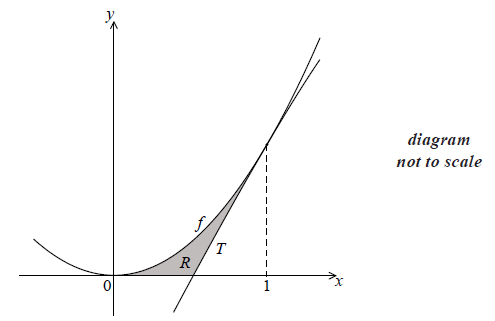
The line T is the tangent to the graph of f at \(x = 1\) .
Show that the equation of T is \(y = 4x – 2\) .
Find the x-intercept of T .
The shaded region R is enclosed by the graph of f , the line T , and the x-axis.
(i) Write down an expression for the area of R .
(ii) Find the area of R .
Answer/Explanation
Markscheme
\(f(1) = 2\) (A1)
\(f'(x) = 4x\) A1
evidence of finding the gradient of f at \(x = 1\) M1
e.g. substituting \(x = 1\) into \(f'(x)\)
finding gradient of f at \(x = 1\) A1
e.g. \(f'(1) = 4\)
evidence of finding equation of the line M1
e.g. \(y – 2 = 4(x – 1)\) , \(2 = 4(1) + b\)
\(y = 4x – 2\) AG N0
[5 marks]
appropriate approach (M1)
e.g. \(4x – 2 = 0\)
\(x = \frac{1}{2}\) A1 N2
[2 marks]
(i) bottom limit \(x = 0\) (seen anywhere) (A1)
approach involving subtraction of integrals/areas (M1)
e.g. \(\int {f(x) – {\text{area of triangle}}} \) , \(\int {f – \int l } \)
correct expression A2 N4
e.g. \(\int_0^1 {2{x^2}{\rm{d}}x – } \int_{0.5}^1 {(4x – 2){\rm{d}}x} \) , \(\int_0^1 {f(x){\rm{d}}x – \frac{1}{2}} \) , \(\int_0^{0.5} {2{x^2}{\rm{d}}x} + \int_{0.5}^1 {(f(x) – (4x – 2)){\rm{d}}x} \)
(ii) METHOD 1 (using only integrals)
correct integration (A1)(A1)(A1)
\(\int {2{x^2}{\rm{d}}x} = \frac{{2{x^3}}}{3}\) , \(\int {(4x – 2){\rm{d}}x = } 2{x^2} – 2x\)
substitution of limits (M1)
e.g. \(\frac{1}{{12}} + \frac{2}{3} – 2 + 2 – \left( {\frac{1}{{12}} – \frac{1}{2} + 1} \right)\)
area = \(\frac{1}{6}\) A1 N4
METHOD 2 (using integral and triangle)
area of triangle = \(\frac{1}{2}\) (A1)
correct integration (A1)
\(\int {2{x^2}{\rm{d}}x = } \frac{{2{x^3}}}{3}\)
substitution of limits (M1)
e.g. \(\frac{2}{3}{(1)^3} – \frac{2}{3}{(0)^3}\) , \(\frac{2}{3} – 0\)
correct simplification (A1)
e.g. \(\frac{2}{3} – \frac{1}{2}\)
area = \(\frac{1}{6}\) A1 N4
[9 marks]
Question
The following is the graph of a function \(f\) , for \(0 \le x \le 6\) .
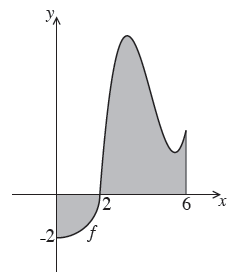
The first part of the graph is a quarter circle of radius \(2\) with centre at the origin.
(a) Find \(\int_0^2 {f(x){\rm{d}}x} \) .
(b) The shaded region is enclosed by the graph of \(f\) , the \(x\)-axis, the \(y\)-axis and the line \(x = 6\) . The area of this region is \(3\pi \) .
Find \(\int_2^6 {f(x){\rm{d}}x} \) .
Find \(\int_0^2 {f(x){\rm{d}}x} \) .
The shaded region is enclosed by the graph of \(f\) , the \(x\)-axis, the \(y\)-axis and the line \(x = 6\) . The area of this region is \(3\pi \) .
Find \(\int_2^6 {f(x){\rm{d}}x} \) .
Answer/Explanation
Markscheme
(a) attempt to find quarter circle area (M1)
eg \(\frac{1}{4}(4\pi )\) , \(\frac{{\pi {r^2}}}{4}\) , \(\int_0^2 {\sqrt {4 – {x^2}{\rm{d}}x} } \)
area of region \( = \pi \) (A1)
\(\int_0^2 {f(x){\rm{d}}x = – \pi } \) A2 N3
[4 marks]
(b) attempted set up with both regions (M1)
eg \({\text{shaded area}} – {\text{quarter circle}}\) , \(3\pi – \pi \) , \(3\pi – \int_0^2 {f = \int_2^6 f } \)
\(\int_2^6 {f(x){\rm{d}}x = 2\pi } \) A2 N2
[3 marks]
Total [7 marks]
attempt to find quarter circle area (M1)
eg \(\frac{1}{4}(4\pi )\) , \(\frac{{\pi {r^2}}}{4}\) , \(\int_0^2 {\sqrt {4 – {x^2}{\rm{d}}x} } \)
area of region \( = \pi \) (A1)
\(\int_0^2 {f(x){\rm{d}}x = – \pi } \) A2 N3
[4 marks]
attempted set up with both regions (M1)
eg \({\text{shaded area}} – {\text{quarter circle}}\) , \(3\pi – \pi \) , \(3\pi – \int_0^2 {f = \int_2^6 f } \)
\(\int_2^6 {f(x){\rm{d}}x = 2\pi } \) A2 N2
[3 marks]
Total [7 marks]