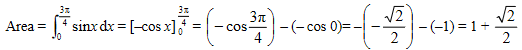Question
(a) The expression \(\frac{3\sqrt{x}-5}{\sqrt{x}}\) can be written as \(3-5x^p\) . Write down the value of p . [1]
(b) Hence, find the value of \(\int_{1}^{9}\frac{3\sqrt{x}-5}{\sqrt{x}}dx\)
Answer/Explanation
Ans

Question
Let f (x) = \(\sqrt{12-2x}\) , x ≤ a . The following diagram shows part of the graph of f .
The shaded region is enclosed by the graph of f , the x-axis and the y-axis.
 x
x
The graph of f intersects the x-axis at the point (a , 0) .
Find the value of a . [2]
Find the volume of the solid formed when the shaded region is revolved 360° about the x-axis. [5]
Answer/Explanation
Ans:
(a)
recognize f (x) = 0
eg \(\sqrt{12-2x}= 0, 2x=12\)
a= 6 (accept x= 6, (6,0))
(b)
attempt to substitute either their limits or the function into volume formula (must involve \(f^{2})\)
eg \(\int_{0}^{6}f^{2}dx , \pi \int (\sqrt{12-2x})^{2}, \pi \int_{0}^{6}\)(12-2x) dx
correct integaration of each term
eg \(12x-x^{2}, 12x-x^{2}\)+c, \(\left [ 12x-x^{2} \right ]_0^6\)
substituting limits into their integrated function and subtracting (in any order)
eg \(\pi (12(6)-(6)^{2})-\pi (0),72\pi -36\pi ,(12(6)-(6)^{2})-(0)\)
volume = \(36\pi \)
Question
Find \(\int {\frac{1}{{2x + 3}}} {\rm{d}}x\) .[2]
Given that \(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \ln \sqrt P \) , find the value of P.[4]
Answer/Explanation
Markscheme
\(\int {\frac{1}{{2x + 3}}} {\rm{d}}x = \frac{1}{2}\ln (2x + 3) + C\) (accept \(\frac{1}{2}\ln |(2x + 3)| + C\) ) A1A1 N2
[2 marks]
\(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \left[ {\frac{1}{2}\ln (2x + 3)} \right]_0^3\)
evidence of substitution of limits (M1)
e.g.\(\frac{1}{2}\ln 9 – \frac{1}{2}\ln 3\)
evidence of correctly using \(\ln a – \ln b = \ln \frac{a}{b}\) (seen anywhere) (A1)
e.g. \(\frac{1}{2}\ln 3\)
evidence of correctly using \(a\ln b = \ln {b^a}\) (seen anywhere) (A1)
e.g. \(\ln \sqrt {\frac{9}{3}} \)
\(P = 3\) (accept \(\ln \sqrt 3 \) ) A1 N2
[4 marks]
Question
Find \(\int_4^{10} {(x – 4){\rm{d}}x} \) .
Part of the graph of \(f(x) = \sqrt {{x^{}} – 4} \) , for \(x \ge 4\) , is shown below. The shaded region R is enclosed by the graph of \(f\) , the line \(x = 10\) , and the x-axis.
The region R is rotated \({360^ \circ }\) about the x-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
correct integration A1A1
e.g. \(\frac{{{x^2}}}{2} – 4x\), \(\left[ {\frac{{{x^2}}}{2} – 4x} \right]_4^{10}\), \(\frac{{{{(x – 4)}^2}}}{2}\)
Notes: In the first 2 examples, award A1 for each correct term.
In the third example, award A1 for \(\frac{1}{2}\) and A1 for \({(x – 4)^2}\).
substituting limits into their integrated function and subtracting (in any order) (M1)
e.g. \(\left( {\frac{{{{10}^2}}}{2} – 4(10)} \right) – \left( {\frac{{{4^2}}}{2} – 4(4)} \right),10 – ( – 8),\frac{1}{2}({6^2} – 0)\)
\(\int_4^{10} {(x – 4){\rm{d}}x = 18} \) A1 N2
attempt to substitute either limits or the function into volume formula (M1)
e.g. \(\pi \int_4^{10} {{f^2}} {\rm{d}}x{\text{, }}{\int_a^b {(\sqrt {x – 4} )} ^2}{\text{, }}\pi \int_4^{10} {\sqrt {x – 4} } \)
Note: Do not penalise for missing \(\pi \) or dx.
correct substitution (accept absence of dx and \(\pi \)) (A1)
e.g. \(\pi {\int_4^{10} {(\sqrt {x – 4} )} ^2}{\text{, }}\pi \int_4^{10} {(x – 4){\rm{d}}x} {\text{, }}\int_4^{10} {(x – 4){\rm{d}}x} \)
volume = \(18\pi \) A1 N2
[3 marks]
Question
The diagram shows part of the curve y = sin x. The shaded region is bounded by the curve and the lines y = 0 and \(x = \frac{3\pi}{4}\).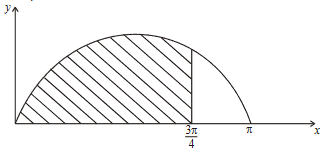
Given that sin \(\frac{3\pi}{4}=\frac{\sqrt{2}}{2}\) and cos \(\frac{3\pi}{4}=-\frac{\sqrt{2}}{2}\), calculate the exact area of the shaded region.
Answer/Explanation
Ans