Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = x{(x – 5)^2}\) , for \(0 \le x \le 6\) . The following diagram shows the graph of f .
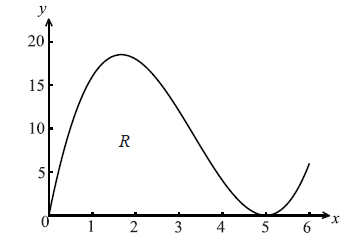
Let R be the region enclosed by the x-axis and the curve of f .
Find the area of R.
Find the volume of the solid formed when R is rotated through \({360^ \circ }\) about the x-axis.
The diagram below shows a part of the graph of a quadratic function \(g(x) = x(a – x)\) . The graph of g crosses the x-axis when \(x = a\) .
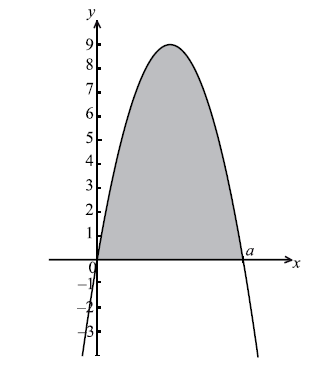
The area of the shaded region is equal to the area of R. Find the value of a.
Answer/Explanation
Markscheme
finding the limits \(x = 0\) , \(x = 5\) (A1)
integral expression A1
e.g. \(\int_0^5 {f(x){\rm{d}}x} \)
area = 52.1 A1 N2
[3 marks]
evidence of using formula \(v = \int {\pi {y^2}{\rm{d}}x} \) (M1)
correct expression A1
e.g. volume \( = \pi \int_0^5 {{x^2}{{(x – 5)}^4}{\rm{d}}x} \)
volume = 2340 A2 N2
[4 marks]
area is \(\int_0^a {x(a – x){\rm{d}}x} \) A1
\( = \left[ {\frac{{a{x^2}}}{2} – \frac{{{x^3}}}{3}} \right]_0^a\) A1A1
substituting limits (M1)
e.g. \(\frac{{{a^3}}}{2} – \frac{{{a^3}}}{3}\)
setting expression equal to area of R (M1)
correct equation A1
e.g. \(\frac{{{a^3}}}{2} – \frac{{{a^3}}}{3} = 52.1\) , \({a^3} = 6 \times 52.1\)
\(a = 6.79\) A1 N3
[7 marks]
Question
Let \(f(x) = {{\rm{e}}^x}\sin 2x + 10\) , for \(0 \le x \le 4\) . Part of the graph of f is given below.
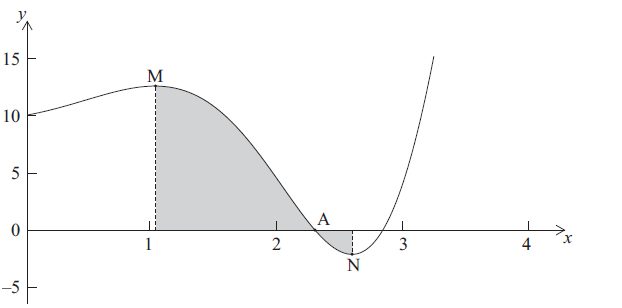
There is an x-intercept at the point A, a local maximum point at M, where \(x = p\) and a local minimum point at N, where \(x = q\) .
Write down the x-coordinate of A.
Find the value of
(i) p ;
(ii) q .
Find \(\int_p^q {f(x){\rm{d}}x} \) . Explain why this is not the area of the shaded region.
Answer/Explanation
Markscheme
\(2.31\) A1 N1
[1 mark]
(i) 1.02 A1 N1
(ii) 2.59 A1 N1
[2 marks]
\(\int_p^q {f(x){\rm{d}}x} = 9.96\) A1 N1
split into two regions, make the area below the x-axis positive R1R1 N2
[3 marks]
Question
The velocity v ms−1 of an object after t seconds is given by \(v(t) = 15\sqrt t – 3t\) , for \(0 \le t \le 25\) .
On the grid below, sketch the graph of v , clearly indicating the maximum point.
(i) Write down an expression for d .
(ii) Hence, write down the value of d .
Answer/Explanation
Markscheme
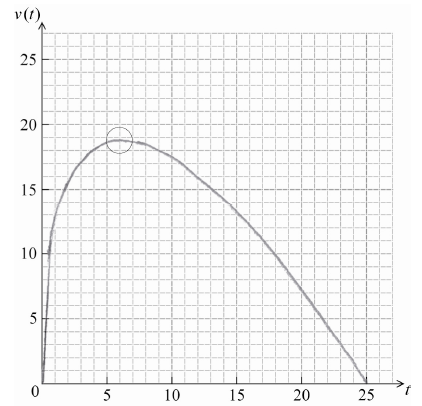A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for right endpoint at \((25{\text{, }}0)\) and A1 for maximum point in circle.
[3 marks]
(i) recognizing that d is the area under the curve (M1)
e.g. \(\int {v(t)} \)
correct expression in terms of t, with correct limits A2 N3
e.g. \(d = \int_0^9 {(15\sqrt t } – 3t){\rm{d}}t\) , \(d = \int_0^9 v {\rm{d}}t\)
(ii) \(d = 148.5\) (m) (accept 149 to 3 sf) A1 N1
[4 marks]
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
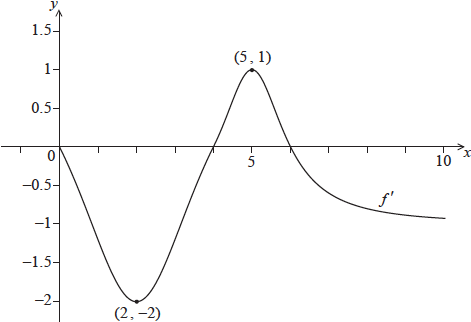
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
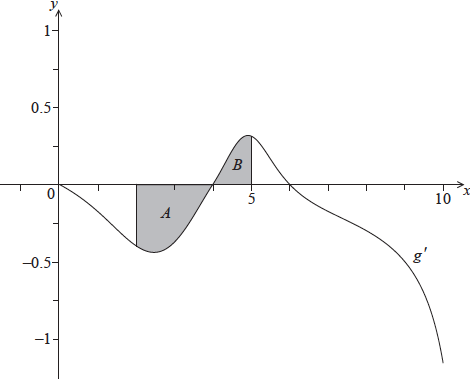
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Question
A particle P moves along a straight line so that its velocity, \(v\,{\text{m}}{{\text{s}}^{ – 1}}\), after \(t\) seconds, is given by \(v = \cos 3t – 2\sin t – 0.5\), for \(0 \leqslant t \leqslant 5\). The initial displacement of P from a fixed point O is 4 metres.
The following sketch shows the graph of \(v\).
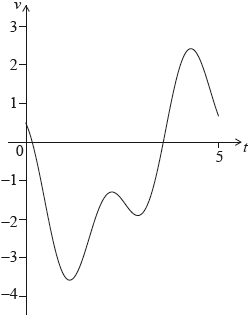
Find the displacement of P from O after 5 seconds.
Find when P is first at rest.
Write down the number of times P changes direction.
Find the acceleration of P after 3 seconds.
Find the maximum speed of P.
Answer/Explanation
Markscheme
METHOD 1
recognizing \(s = \int v \) (M1)
recognizing displacement of P in first 5 seconds (seen anywhere) A1
(accept missing \({\text{d}}t\))
eg\(\,\,\,\,\,\)\(\int_0^5 {v{\text{d}}t,{\text{ }} – 3.71591} \)
valid approach to find total displacement (M1)
eg\(\,\,\,\,\,\)\(4 + ( – 3.7159),{\text{ }}s = 4 + \int_0^5 v \)
0.284086
0.284 (m) A2 N3
METHOD 2
recognizing \(s = \int v \) (M1)
correct integration A1
eg\(\,\,\,\,\,\)\(\frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c\) (do not penalize missing “\(c\)”)
attempt to find \(c\) (M1)
eg\(\,\,\,\,\,\)\(4 = \frac{1}{3}\sin (0) + 2\cos (0)–\frac{0}{2} + c,{\text{ }}4 = \frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c,{\text{ }}2 + c = 4\)
attempt to substitute \(t = 5\) into their expression with \(c\) (M1)
eg\(\,\,\,\,\,\)\(s(5),{\text{ }}\frac{1}{3}\sin (15) + 2\cos (5)5–\frac{5}{2} + 2\)
0.284086
0.284 (m) A1 N3
[5 marks]
recognizing that at rest, \(v = 0\) (M1)
\(t = 0.179900\)
\(t = 0.180{\text{ (secs)}}\) A1 N2
[2 marks]
recognizing when change of direction occurs (M1)
eg\(\,\,\,\,\,\)\(v\) crosses \(t\) axis
2 (times) A1 N2
[2 marks]
acceleration is \({v’}\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(v'(3)\)
0.743631
\(0.744{\text{ }}({\text{m}}{{\text{s}}^{ – 2}})\) A1 N2
[2 marks]
valid approach involving max or min of \(v\) (M1)
eg\(\,\,\,\,\,\)\(v\prime = 0,{\text{ }}a = 0\), graph
one correct co-ordinate for min (A1)
eg\(\,\,\,\,\,\)\(1.14102,{\text{ }}-3.27876\)
\(3.28{\text{ }}({\text{m}}{{\text{s}}^{ – 1}})\) A1 N2
[3 marks]
Question
A particle moves in a straight line. Its velocity \(v{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v = 6t – 6,{\text{ for }}0 \leqslant t \leqslant 2.\]
After \(p\) seconds, the particle is 2 m from its initial position. Find the possible values of \(p\).
Answer/Explanation
Markscheme
correct approach (A1)
eg\(\,\,\,\,\,\)\(s = \int {v,{\text{ }}\int_0^p {6t – 6{\text{d}}t} } \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\int {6t – 6{\text{d}}t = 3{t^2} – 6t + C,{\text{ }}\left[ {3{t^2} – 6t} \right]_0^p} \)
recognizing that there are two possibilities (M1)
eg\(\,\,\,\,\,\)2 correct answers, \(s = \pm 2,{\text{ }}c \pm 2\)
two correct equations in \(p\) A1A1
eg\(\,\,\,\,\,\)\(3{p^2} – 6p = 2,{\text{ }}3{p^2} – 6p = – 2\)
0.42265, 1.57735
\(p = 0.423{\text{ or }}p = 1.58\) A1A1 N3
[7 marks]
Question
A particle P starts from a point A and moves along a horizontal straight line. Its velocity \(v{\text{ cm}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v(t) = \left\{ {\begin{array}{*{20}{l}} { – 2t + 2,}&{{\text{for }}0 \leqslant t \leqslant 1} \\ {3\sqrt t + \frac{4}{{{t^2}}} – 7,}&{{\text{for }}1 \leqslant t \leqslant 12} \end{array}} \right.\]
The following diagram shows the graph of \(v\).
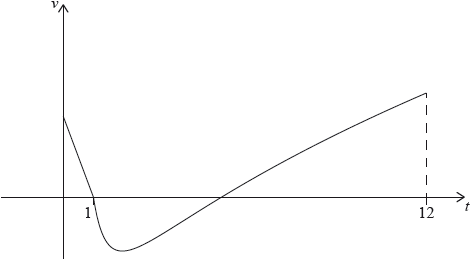
P is at rest when \(t = 1\) and \(t = p\).
When \(t = q\), the acceleration of P is zero.
Find the initial velocity of \(P\).
Find the value of \(p\).
(i) Find the value of \(q\).
(ii) Hence, find the speed of P when \(t = q\).
(i) Find the total distance travelled by P between \(t = 1\) and \(t = p\).
(ii) Hence or otherwise, find the displacement of P from A when \(t = p\).
Answer/Explanation
Markscheme
valid attempt to substitute \(t = 0\) into the correct function (M1)
eg\(\,\,\,\,\,\)\( – 2(0) + 2\)
2 A1 N2
[2 marks]
recognizing \(v = 0\) when P is at rest (M1)
5.21834
\(p = 5.22{\text{ }}({\text{seconds}})\) A1 N2
[2 marks]
(i) recognizing that \(a = v’\) (M1)
eg\(\,\,\,\,\,\)\(v’ = 0\), minimum on graph
1.95343
\(q = 1.95\) A1 N2
(ii) valid approach to find their minimum (M1)
eg\(\,\,\,\,\,\)\(v(q),{\text{ }} – 1.75879\), reference to min on graph
1.75879
speed \( = 1.76{\text{ }}(c\,{\text{m}}\,{{\text{s}}^{ – 1}})\) A1 N2
[4 marks]
(i) substitution of correct \(v(t)\) into distance formula, (A1)
eg\(\,\,\,\,\,\)\(\int_1^p {\left| {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right|{\text{d}}t,{\text{ }}\left| {\int {3\sqrt t + \frac{4}{{{t^2}}} – 7{\text{d}}t} } \right|} \)
4.45368
distance \( = 4.45{\text{ }}({\text{cm}})\) A1 N2
(ii) displacement from \(t = 1\) to \(t = p\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\( – 4.45368,{\text{ }}\int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t} \)
displacement from \(t = 0\) to \(t = 1\) (A1)
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t,{\text{ }}0.5 \times 1 \times 2,{\text{ 1}}} \)
valid approach to find displacement for \(0 \leqslant t \leqslant p\) M1
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t + \int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t,{\text{ }}\int_0^1 {( – 2t + 2){\text{d}}t – 4.45} } } \)
\( – 3.45368\)
displacement \( = – 3.45{\text{ }}({\text{cm}})\) A1 N2
[6 marks]
Question
A particle P moves along a straight line. Its velocity \({v_{\text{P}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{P}}} = \sqrt t \sin \left( {\frac{\pi }{2}t} \right)\), for \(0 \leqslant t \leqslant 8\). The following diagram shows the graph of \({v_{\text{P}}}\).
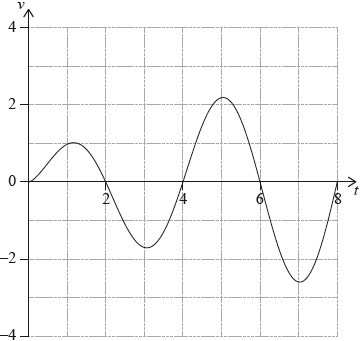
Write down the first value of \(t\) at which P changes direction.
Find the total distance travelled by P, for \(0 \leqslant t \leqslant 8\).
A second particle Q also moves along a straight line. Its velocity, \({v_{\text{Q}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{Q}}} = \sqrt t \) for \(0 \leqslant t \leqslant 8\). After \(k\) seconds Q has travelled the same total distance as P.
Find \(k\).
Answer/Explanation
Markscheme
\(t = 2\) A1 N1
[1 mark]
substitution of limits or function into formula or correct sum (A1)
eg\(\,\,\,\,\,\)\(\int_0^8 {\left| v \right|{\text{d}}t,{\text{ }}\int {\left| {{v_Q}} \right|{\text{d}}t,{\text{ }}\int_0^2 {v{\text{d}}t – \int_2^4 {v{\text{d}}t + \int_4^6 {v{\text{d}}t – \int_6^8 {v{\text{d}}t} } } } } } \)
9.64782
distance \( = 9.65{\text{ (metres)}}\) A1 N2
[2 marks]
correct approach (A1)
eg\(\,\,\,\,\,\)\(s = \int {\sqrt t ,{\text{ }}\int_0^k {\sqrt t } } {\text{d}}t,{\text{ }}\int_0^k {\left| {{v_{\text{Q}}}} \right|{\text{d}}t} \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\int {\sqrt t = \frac{2}{3}{t^{\frac{3}{2}}} + c,{\text{ }}\left[ {\frac{2}{3}{x^{\frac{3}{2}}}} \right]_0^k,{\text{ }}\frac{2}{3}{k^{\frac{3}{2}}}} \)
equating their expression to the distance travelled by their P (M1)
eg\(\,\,\,\,\,\)\(\frac{2}{3}{k^{\frac{3}{2}}} = 9.65,{\text{ }}\int_0^k {\sqrt t {\text{d}}t = 9.65} \)
5.93855
5.94 (seconds) A1 N3
[4 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
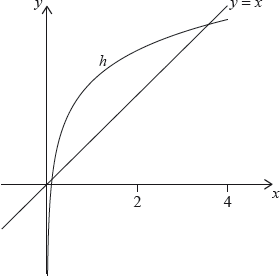
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)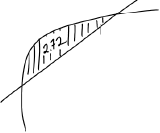
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]
Question
Note: In this question, distance is in metres and time is in seconds.
A particle moves along a horizontal line starting at a fixed point A. The velocity \(v\) of the particle, at time \(t\), is given by \(v(t) = \frac{{2{t^2} – 4t}}{{{t^2} – 2t + 2}}\), for \(0 \leqslant t \leqslant 5\). The following diagram shows the graph of \(v\)
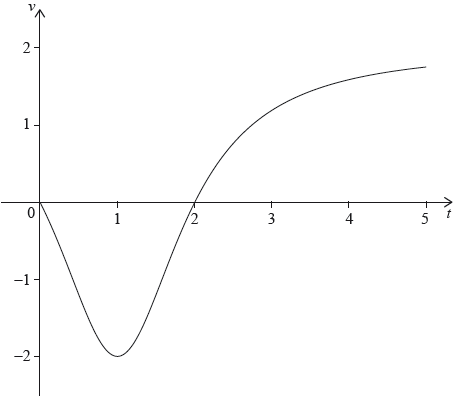
There are \(t\)-intercepts at \((0,{\text{ }}0)\) and \((2,{\text{ }}0)\).
Find the maximum distance of the particle from A during the time \(0 \leqslant t \leqslant 5\) and justify your answer.
Answer/Explanation
Markscheme
METHOD 1 (displacement)
recognizing \(s = \int {v{\text{d}}t} \) (M1)
consideration of displacement at \(t = 2\) and \(t = 5\) (seen anywhere) M1
eg\(\,\,\,\,\,\)\(\int_0^2 v \) and \(\int_0^5 v \)
Note: Must have both for any further marks.
correct displacement at \(t = 2\) and \(t = 5\) (seen anywhere) A1A1
\( – 2.28318\) (accept 2.28318), 1.55513
valid reasoning comparing correct displacements R1
eg\(\,\,\,\,\,\)\(\left| { – 2.28} \right| > \left| {1.56} \right|\), more left than right
2.28 (m) A1 N1
Note: Do not award the final A1 without the R1.
METHOD 2 (distance travelled)
recognizing distance \( = \int {\left| v \right|{\text{d}}t} \) (M1)
consideration of distance travelled from \(t = 0\) to 2 and \(t = 2\) to 5 (seen anywhere) M1
eg\(\,\,\,\,\,\)\(\int_0^2 v \) and \(\int_2^5 v \)
Note: Must have both for any further marks
correct distances travelled (seen anywhere) A1A1
2.28318, (accept \( – 2.28318\)), 3.83832
valid reasoning comparing correct distance values R1
eg\(\,\,\,\,\,\)\(3.84 – 2.28 < 2.28,{\text{ }}3.84 < 2 \times 2.28\)
2.28 (m) A1 N1
Note: Do not award the final A1 without the R1.
[6 marks]
Question
Let \(f(x) = – 0.5{x^4} + 3{x^2} + 2x\). The following diagram shows part of the graph of \(f\).
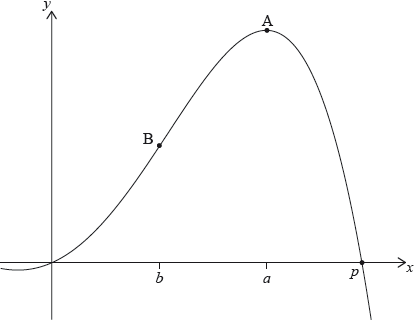
There are \(x\)-intercepts at \(x = 0\) and at \(x = p\). There is a maximum at A where \(x = a\), and a point of inflexion at B where \(x = b\).
Find the value of \(p\).
Write down the coordinates of A.
Write down the rate of change of \(f\) at A.
Find the coordinates of B.
Find the the rate of change of \(f\) at B.
Let \(R\) be the region enclosed by the graph of \(f\) , the \(x\)-axis, the line \(x = b\) and the line \(x = a\). The region \(R\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }}y = 0\)
2.73205
\(p = 2.73\) A1 N2
[2 marks]
1.87938, 8.11721
\((1.88,{\text{ }}8.12)\) A2 N2
[2 marks]
rate of change is 0 (do not accept decimals) A1 N1
[1 marks]
METHOD 1 (using GDC)
valid approach M1
eg\(\,\,\,\,\,\)\(f’’ = 0\), max/min on \(f’,{\text{ }}x = – 1\)
sketch of either \(f’\) or \(f’’\), with max/min or root (respectively) (A1)
\(x = 1\) A1 N1
Substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
METHOD 2 (analytical)
\(f’’ = – 6{x^2} + 6\) A1
setting \(f’’ = 0\) (M1)
\(x = 1\) A1 N1
substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
[4 marks]
recognizing rate of change is \(f’\) (M1)
eg\(\,\,\,\,\,\)\(y’,{\text{ }}f’(1)\)
rate of change is 6 A1 N2
[3 marks]
attempt to substitute either limits or the function into formula (M1)
involving \({f^2}\) (accept absence of \(\pi \) and/or \({\text{d}}x\))
eg\(\,\,\,\,\,\)\(\pi \int {{{( – 0.5{x^4} + 3{x^2} + 2x)}^2}{\text{d}}x,{\text{ }}\int_1^{1.88} {{f^2}} } \)
128.890
\({\text{volume}} = 129\) A2 N3
[3 marks]
Question
Note: In this question, distance is in metres and time is in seconds.
A particle P moves in a straight line for five seconds. Its acceleration at time \(t\) is given by \(a = 3{t^2} – 14t + 8\), for \(0 \leqslant t \leqslant 5\).
When \(t = 0\), the velocity of P is \(3{\text{ m}}\,{{\text{s}}^{ – 1}}\).
Write down the values of \(t\) when \(a = 0\).
Hence or otherwise, find all possible values of \(t\) for which the velocity of P is decreasing.
Find an expression for the velocity of P at time \(t\).
Find the total distance travelled by P when its velocity is increasing.
Answer/Explanation
Markscheme
\(t = \frac{2}{3}{\text{ (exact), }}0.667,{\text{ }}t = 4\) A1A1 N2
[2 marks]
recognizing that \(v\) is decreasing when \(a\) is negative (M1)
eg\(\,\,\,\,\,\)\(a < 0,{\text{ }}3{t^2} – 14t + 8 \leqslant 0\), sketch of \(a\)
correct interval A1 N2
eg\(\,\,\,\,\,\)\(\frac{2}{3} < t < 4\)
[2 marks]
valid approach (do not accept a definite integral) (M1)
eg\(\,\,\,\,\,\)\(v\int a \)
correct integration (accept missing \(c\)) (A1)(A1)(A1)
\({t^3} – 7{t^2} + 8t + c\)
substituting \(t = 0,{\text{ }}v = 3\) , (must have \(c\)) (M1)
eg\(\,\,\,\,\,\)\(3 = {0^3} – 7({0^2}) + 8(0) + c,{\text{ }}c = 3\)
\(v = {t^3} – 7{t^2} + 8t + 3\) A1 N6
[6 marks]
recognizing that \(v\) increases outside the interval found in part (b) (M1)
eg\(\,\,\,\,\,\)\(0 < t < \frac{2}{3},{\text{ }}4 < t < 5\), diagram
one correct substitution into distance formula (A1)
eg\(\,\,\,\,\,\)\(\int_0^{\frac{2}{3}} {\left| v \right|,{\text{ }}\int_4^5 {\left| v \right|} ,{\text{ }}\int_{\frac{2}{3}}^4 {\left| v \right|} ,{\text{ }}\int_0^5 {\left| v \right|} } \)
one correct pair (A1)
eg\(\,\,\,\,\,\)3.13580 and 11.0833, 20.9906 and 35.2097
14.2191 A1 N2
\(d = 14.2{\text{ (m)}}\)
[4 marks]