Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = x\cos (x – \sin x)\) , \(0 \le x \le 3\) .
Sketch the graph of f on the following set of axes.
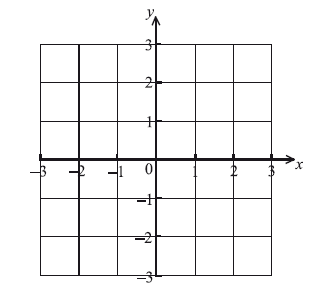
The graph of f intersects the x-axis when \(x = a\) , \(a \ne 0\) . Write down the value of a.
The graph of f is revolved \(360^\circ \) about the x-axis from \(x = 0\) to \(x = a\) . Find the volume of the solid formed.
Answer/Explanation
Markscheme
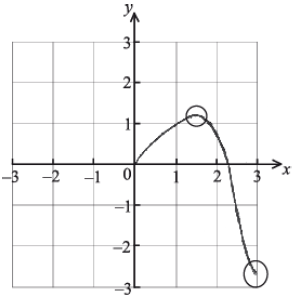A1A2 N3
Notes: Award A1 for correct domain, \(0 \le x \le 3\) . Award A2 for approximately correct shape, with local maximum in circle 1 and right endpoint in circle 2.
[3 marks]
\(a = 2.31\) A1 N1
[1 mark]
evidence of using \(V = \pi {\int {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) (M1)
fully correct integral expression A2
e.g. \(V = \pi {\int_0^{2.31} {\left[ {x\cos (x – \sin x)} \right]} ^2}{\rm{d}}x\) , \(V = \pi {\int_0^{2.31} {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) A1 N2
\(V = 5.90\)
[4 marks]
Question
Let \(f(x) = x{(x – 5)^2}\) , for \(0 \le x \le 6\) . The following diagram shows the graph of f .
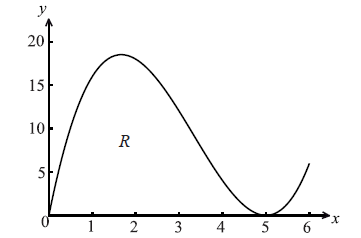
Let R be the region enclosed by the x-axis and the curve of f .
Find the area of R.
Find the volume of the solid formed when R is rotated through \({360^ \circ }\) about the x-axis.
The diagram below shows a part of the graph of a quadratic function \(g(x) = x(a – x)\) . The graph of g crosses the x-axis when \(x = a\) .
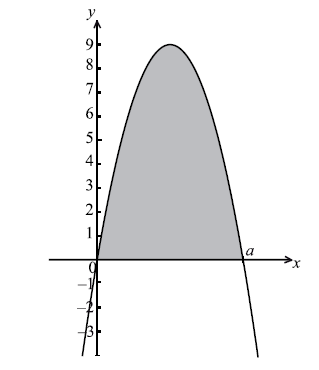
The area of the shaded region is equal to the area of R. Find the value of a.
Answer/Explanation
Markscheme
finding the limits \(x = 0\) , \(x = 5\) (A1)
integral expression A1
e.g. \(\int_0^5 {f(x){\rm{d}}x} \)
area = 52.1 A1 N2
[3 marks]
evidence of using formula \(v = \int {\pi {y^2}{\rm{d}}x} \) (M1)
correct expression A1
e.g. volume \( = \pi \int_0^5 {{x^2}{{(x – 5)}^4}{\rm{d}}x} \)
volume = 2340 A2 N2
[4 marks]
area is \(\int_0^a {x(a – x){\rm{d}}x} \) A1
\( = \left[ {\frac{{a{x^2}}}{2} – \frac{{{x^3}}}{3}} \right]_0^a\) A1A1
substituting limits (M1)
e.g. \(\frac{{{a^3}}}{2} – \frac{{{a^3}}}{3}\)
setting expression equal to area of R (M1)
correct equation A1
e.g. \(\frac{{{a^3}}}{2} – \frac{{{a^3}}}{3} = 52.1\) , \({a^3} = 6 \times 52.1\)
\(a = 6.79\) A1 N3
[7 marks]
Question
Let \(f(x) = x\ln (4 – {x^2})\) , for \( – 2 < x < 2\) . The graph of f is shown below.
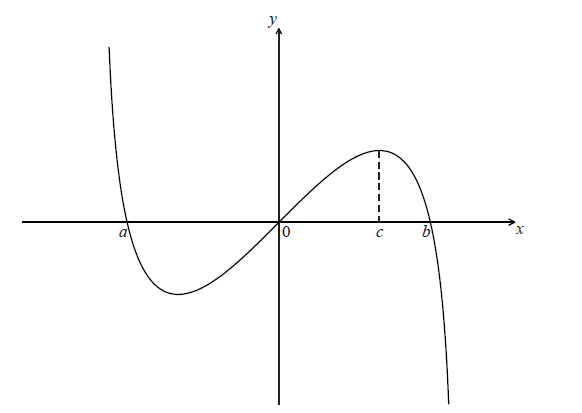
The graph of f crosses the x-axis at \(x = a\) , \(x = 0\) and \(x = b\) .
Find the value of a and of b .
The graph of f has a maximum value when \(x = c\) .
Find the value of c .
The region under the graph of f from \(x = 0\) to \(x = c\) is rotated \({360^ \circ }\) about the x-axis. Find the volume of the solid formed.
Let R be the region enclosed by the curve, the x-axis and the line \(x = c\) , between \(x = a\) and \(x = c\) .
Find the area of R .
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(f(x) = 0\) , graph
\(a = – 1.73\) , \(b = 1.73\) \((a = – \sqrt 3 {\text{, }}b = \sqrt 3 )\) A1A1 N3
[3 marks]
attempt to find max (M1)
e.g. setting \(f'(x) = 0\) , graph
\(c = 1.15\) (accept (1.15, 1.13)) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula M1
e.g. \(V = \pi {\int_0^c {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) , \(\pi {\int {\left[ {x\ln (4 – {x^2})} \right]} ^2}\) , \(\pi \int_0^{1.149 \ldots } {{y^2}{\rm{d}}x} \)
\(V = 2.16\) A2 N2
[3 marks]
valid approach recognizing 2 regions (M1)
e.g. finding 2 areas
correct working (A1)
e.g. \(\int_0^{ – 1.73 \ldots } {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \) , \( – \int_{ – 1.73 \ldots }^0 {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \)
area \( = 2.07\) (accept 2.06) A2 N3
[4 marks]
Question
The graph of \(y = (x – 1)\sin x\) , for \(0 \le x \le \frac{{5\pi }}{2}\) , is shown below.
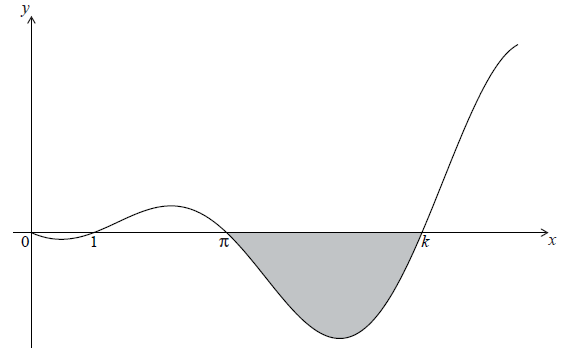
The graph has \(x\)-intercepts at \(0\), \(1\), \( \pi\) and \(k\) .
Find k .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Write down an expression for V .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Find V .
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(y = 0\) , \(\sin x = 0\)
\(2\pi = 6.283185 \ldots \)
\(k = 6.28\) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula (M1)
(accept absence of \({\rm{d}}x\) )
e.g. \(V = \pi \int_\pi ^k {{{(f(x))}^2}{\rm{d}}x} \) , \(\pi \int {{{((x – 1)\sin x)}^2}} \) , \(\pi \int_\pi ^{6.28 \ldots } {{y^2}{\rm{d}}x} \)
correct expression A2 N3
e.g. \(\pi \int_\pi ^{6.28} {{{(x – 1)}^2}{{\sin }^2}x{\rm{d}}x} \) , \(\pi \int_\pi ^{2\pi } {{{((x – 1)\sin x)}^2}{\rm{d}}x} \)
[3 marks]
\(V = 69.60192562 \ldots \)
\(V = 69.6\) A2 N2
[2 marks]
Question
Let \(f(x) = (x – 1)(x – 4)\).
Find the \(x\)-intercepts of the graph of \(f\).
The region enclosed by the graph of \(f\) and the \(x\)-axis is rotated \(360^\circ\) about the \(x\)-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(f(x) = 0\), sketch of parabola showing two \(x\)-intercepts
\(x = 1,{\text{ }}x = 4{\text{ }}\left( {{\text{accept (1, 0), (4, 0)}}} \right)\) A1A1 N3
[3 marks]
attempt to substitute either limits or the function into formula involving \({f^2}\) (M1)
eg \(\int_1^4 {{{\left( {f(x)} \right)}^2}{\text{d}}x,{\text{ }}\pi \int {{{\left( {(x – 1)(x – 4)} \right)}^2}} } \)
\({\text{volume}} = 8.1\pi {\text{ (exact), 25.4}}\) A2 N3
[3 marks]
Question
Let \(f(x) = 5 – {x^2}\). Part of the graph of \(f\)is shown in the following diagram.
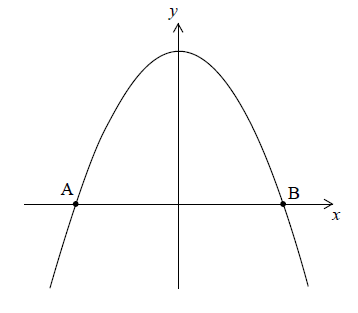
The graph crosses the \(x\)-axis at the points \(\rm{A}\) and \(\rm{B}\).
Find the \(x\)-coordinate of \({\text{A}}\) and of \({\text{B}}\).
The region enclosed by the graph of \(f\) and the \(x\)-axis is revolved \(360^\circ \) about the \(x\)-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
recognizing \(f(x) = 0\) (M1)
eg \(f = 0,{\text{ }}{x^2} = 5\)
\(x = \pm 2.23606\)
\(x = \pm \sqrt 5 {\text{ (exact), }}x = \pm 2.24\) A1A1 N3
[3 marks]
attempt to substitute either limits or the function into formula
involving \({f^2}\) (M1)
eg \(\pi \int {{{\left( {5 – {x^2}} \right)}^2}{\text{d}}x,{\text{ }}\pi \int_{ – 2.24}^{2.24} {\left( {{x^4} – 10{x^2} + 25} \right)} ,{\text{ }}2\pi \int_0^{\sqrt 5 } {{f^2}} } \)
\(187.328\)
volume \(= 187\) A2 N3
[3 marks]
Question
Let \(f(x) = – {x^4} + 2{x^3} – 1\), for \(0 \le x \le 2\).
Sketch the graph of \(f\) on the following grid.
Solve \(f(x) = 0\).
The region enclosed by the graph of \(f\) and the \(x\)-axis is rotated \(360°\) about the \(x\)-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for both endpoints in circles,
A1 for approximately correct shape (concave up to concave down).
Only if this A1 for shape is awarded, award A1 for maximum point in circle.
\(x = 1\;\;\;x = 1.83928\)
\(x = 1{\text{ (exact)}}\;\;\;x = 1.84{\text{ }}[1.83,{\text{ }}1.84]\) A1A1 N2
[2 marks]
attempt to substitute either (FT ) limits or function into formula with \({f^2}\) (M1)
eg\(\;\;\;\)\(V = \pi \int_1^{1.84} {{f^2},{\text{ }}\int {{{( – {x^4} + 2{x^3} – 1)}^2}{\text{d}}x} } \)
\(0.636581\)
\(V = 0.637{\text{ }}[0.636,{\text{ }}0.637]\) A2 N3
[3 marks]
Total [8 marks]
Question
Let \(f(x) = 2\ln (x – 3)\), for \(x > 3\). The following diagram shows part of the graph of \(f\).
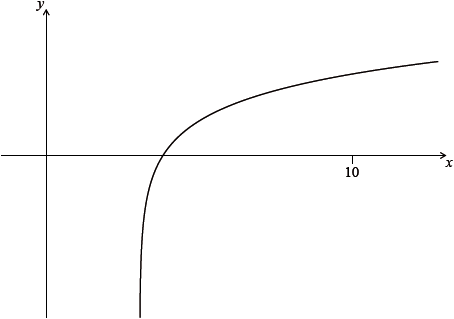
Find the equation of the vertical asymptote to the graph of \(f\).
Find the \(x\)-intercept of the graph of \(f\).
The region enclosed by the graph of \(f\), the \(x\)-axis and the line \(x = 10\) is rotated \(360\)° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)horizontal translation \(3\) units to the right
\(x = 3\) (must be an equation) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;f(x) = 0,{\text{ }}{e^0} = x – 3\)
\(4,{\text{ }}x = 4,{\text{ }}(4,{\text{ }}0)\) A1 N2
[2 marks]
attempt to substitute either their correct limits or the function into formula involving \({f^2}\) (M1)
eg\(\;\;\;\int_4^{10} {{f^2},{\text{ }}\pi \int {{{\left( {2\ln (x – 3)} \right)}^2}{\text{d}}x} } \)
\(141.537\)
volume = \(142\) A2 N3
[3 marks]
Total [7 marks]
Question
All lengths in this question are in metres.
Let \(f(x) = – 0.8{x^2} + 0.5\), for \( – 0.5 \leqslant x \leqslant 0.5\). Mark uses \(f(x)\) as a model to create a barrel. The region enclosed by the graph of \(f\), the \(x\)-axis, the line \(x = – 0.5\) and the line \(x = 0.5\) is rotated 360° about the \(x\)-axis. This is shown in the following diagram.
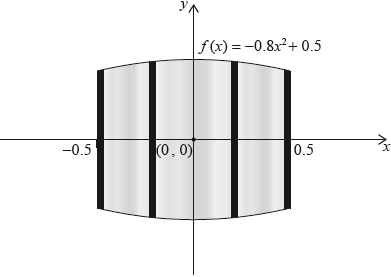
Use the model to find the volume of the barrel.
The empty barrel is being filled with water. The volume \(V{\text{ }}{{\text{m}}^3}\) of water in the barrel after \(t\) minutes is given by \(V = 0.8(1 – {{\text{e}}^{ – 0.1t}})\). How long will it take for the barrel to be half-full?
Answer/Explanation
Markscheme
attempt to substitute correct limits or the function into the formula involving
\({y^2}\)
eg\(\,\,\,\,\,\)\(\pi \int_{ – 0.5}^{0.5} {{y^2}{\text{d}}x,{\text{ }}\pi \int {{{( – 0.8{x^2} + 0.5)}^2}{\text{d}}x} } \)
0.601091
volume \( = 0.601{\text{ }}({{\text{m}}^3})\) A2 N3
[3 marks]
attempt to equate half their volume to \(V\) (M1)
eg\(\,\,\,\,\,\)\(0.30055 = 0.8(1 – {{\text{e}}^{ – 0.1t}})\), graph
4.71104
4.71 (minutes) A2 N3
[3 marks]
Question
A particle P starts from a point A and moves along a horizontal straight line. Its velocity \(v{\text{ cm}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v(t) = \left\{ {\begin{array}{*{20}{l}} { – 2t + 2,}&{{\text{for }}0 \leqslant t \leqslant 1} \\ {3\sqrt t + \frac{4}{{{t^2}}} – 7,}&{{\text{for }}1 \leqslant t \leqslant 12} \end{array}} \right.\]
The following diagram shows the graph of \(v\).
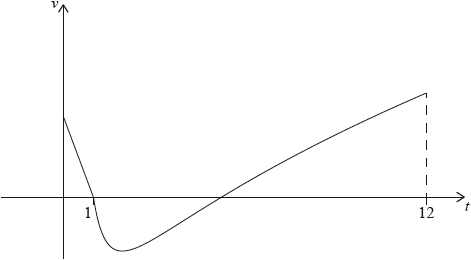
P is at rest when \(t = 1\) and \(t = p\).
When \(t = q\), the acceleration of P is zero.
Find the initial velocity of \(P\).
Find the value of \(p\).
(i) Find the value of \(q\).
(ii) Hence, find the speed of P when \(t = q\).
(i) Find the total distance travelled by P between \(t = 1\) and \(t = p\).
(ii) Hence or otherwise, find the displacement of P from A when \(t = p\).
Answer/Explanation
Markscheme
valid attempt to substitute \(t = 0\) into the correct function (M1)
eg\(\,\,\,\,\,\)\( – 2(0) + 2\)
2 A1 N2
[2 marks]
recognizing \(v = 0\) when P is at rest (M1)
5.21834
\(p = 5.22{\text{ }}({\text{seconds}})\) A1 N2
[2 marks]
(i) recognizing that \(a = v’\) (M1)
eg\(\,\,\,\,\,\)\(v’ = 0\), minimum on graph
1.95343
\(q = 1.95\) A1 N2
(ii) valid approach to find their minimum (M1)
eg\(\,\,\,\,\,\)\(v(q),{\text{ }} – 1.75879\), reference to min on graph
1.75879
speed \( = 1.76{\text{ }}(c\,{\text{m}}\,{{\text{s}}^{ – 1}})\) A1 N2
[4 marks]
(i) substitution of correct \(v(t)\) into distance formula, (A1)
eg\(\,\,\,\,\,\)\(\int_1^p {\left| {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right|{\text{d}}t,{\text{ }}\left| {\int {3\sqrt t + \frac{4}{{{t^2}}} – 7{\text{d}}t} } \right|} \)
4.45368
distance \( = 4.45{\text{ }}({\text{cm}})\) A1 N2
(ii) displacement from \(t = 1\) to \(t = p\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\( – 4.45368,{\text{ }}\int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t} \)
displacement from \(t = 0\) to \(t = 1\) (A1)
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t,{\text{ }}0.5 \times 1 \times 2,{\text{ 1}}} \)
valid approach to find displacement for \(0 \leqslant t \leqslant p\) M1
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t + \int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t,{\text{ }}\int_0^1 {( – 2t + 2){\text{d}}t – 4.45} } } \)
\( – 3.45368\)
displacement \( = – 3.45{\text{ }}({\text{cm}})\) A1 N2
[6 marks]
Question
Let \(f(x) = – 0.5{x^4} + 3{x^2} + 2x\). The following diagram shows part of the graph of \(f\).
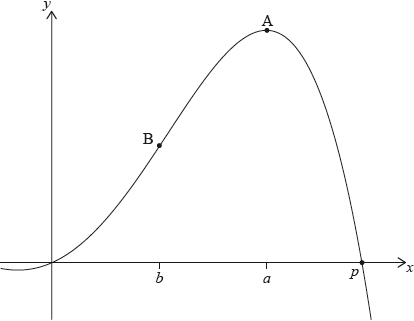
There are \(x\)-intercepts at \(x = 0\) and at \(x = p\). There is a maximum at A where \(x = a\), and a point of inflexion at B where \(x = b\).
Find the value of \(p\).
Write down the coordinates of A.
Write down the rate of change of \(f\) at A.
Find the coordinates of B.
Find the the rate of change of \(f\) at B.
Let \(R\) be the region enclosed by the graph of \(f\) , the \(x\)-axis, the line \(x = b\) and the line \(x = a\). The region \(R\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }}y = 0\)
2.73205
\(p = 2.73\) A1 N2
[2 marks]
1.87938, 8.11721
\((1.88,{\text{ }}8.12)\) A2 N2
[2 marks]
rate of change is 0 (do not accept decimals) A1 N1
[1 marks]
METHOD 1 (using GDC)
valid approach M1
eg\(\,\,\,\,\,\)\(f’’ = 0\), max/min on \(f’,{\text{ }}x = – 1\)
sketch of either \(f’\) or \(f’’\), with max/min or root (respectively) (A1)
\(x = 1\) A1 N1
Substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
METHOD 2 (analytical)
\(f’’ = – 6{x^2} + 6\) A1
setting \(f’’ = 0\) (M1)
\(x = 1\) A1 N1
substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
[4 marks]
recognizing rate of change is \(f’\) (M1)
eg\(\,\,\,\,\,\)\(y’,{\text{ }}f’(1)\)
rate of change is 6 A1 N2
[3 marks]
attempt to substitute either limits or the function into formula (M1)
involving \({f^2}\) (accept absence of \(\pi \) and/or \({\text{d}}x\))
eg\(\,\,\,\,\,\)\(\pi \int {{{( – 0.5{x^4} + 3{x^2} + 2x)}^2}{\text{d}}x,{\text{ }}\int_1^{1.88} {{f^2}} } \)
128.890
\({\text{volume}} = 129\) A2 N3
[3 marks]
Question
Let \(f\left( x \right) = \,\,{\text{sin}}\,\left( {{e^x}} \right)\) for 0 ≤ \(x\) ≤ 1.5. The following diagram shows the graph of \(f\).
Find the x-intercept of the graph of \(f\).
The region enclosed by the graph of \(f\), the y-axis and the x-axis is rotated 360° about the x-axis.
Find the volume of the solid formed.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(f\left( x \right) = 0,\,\,\,\,{e^x} = 180\) or 0…
1.14472
\(x = {\text{ln}}\,\pi \) (exact), 1.14 A1 N2
[2 marks]
attempt to substitute either their limits or the function into formula involving \({f^2}\). (M1)
eg \({\int_0^{1.14} {{f^2},\,\,\pi \int {\left( {{\text{sin}}\,\left( {{e^x}} \right)} \right)} } ^2}dx,\,\,0.795135\)
2.49799
volume = 2.50 A2 N3
[3 marks]
Question
Let \(h(x) = \frac{{2x – 1}}{{x + 1}}\) , \(x \ne – 1\) .
Find \({h^{ – 1}}(x)\) .
(i) Sketch the graph of h for \( – 4 \le x \le 4\) and \( – 5 \le y \le 8\) , including any asymptotes.
(ii) Write down the equations of the asymptotes.
(iii) Write down the x-intercept of the graph of h .
Let R be the region in the first quadrant enclosed by the graph of h , the x-axis and the line \(x = 3\).
(i) Find the area of R.
(ii) Write down an expression for the volume obtained when R is revolved through \({360^ \circ }\) about the x-axis.
Answer/Explanation
Markscheme
\(y = \frac{{2x – 1}}{{x + 1}}\)
interchanging x and y (seen anywhere) M1
e.g. \(x = \frac{{2y – 1}}{{y + 1}}\)
correct working A1
e.g. \(xy + x = 2y – 1\)
collecting terms A1
e.g. \(x + 1 = 2y – xy\) , \(x + 1 = y(2 – x)\)
\({h^{ – 1}}(x) = \frac{{x + 1}}{{2 – x}}\) A1 N2
[4 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct intercepts, A1 for correct shape, A1 for asymptotes, A1 for approximately correct domain and range.
(ii) \(x = – 1\) , \(y = 2\) A1A1 N2
(iii) \(\frac{1}{2}\) A1 N1
[7 marks]
(i) \({\text{area}} = 2.06\) A2 N2
(ii) attempt to substitute into volume formula (do not accept \(\pi \int_a^b {{y^2}{\rm{d}}x} \) ) M1
volume \( = \pi {\int_{\frac{1}{2}}^3 {\left( {\frac{{2x – 1}}{{x + 1}}} \right)} ^2}{\rm{d}}x\) A2 N3
[5 marks]