Question
An object moves along a straight line. Its velocity, \(vms^{-1}\), at time t seconds is given by
v(t) = -\(t^2 + \frac{7}{2}t^2 + 6\), for 0 ≤ t ≤ 4. The object first comes to rest at t = k .
The graph of v is shown in the following diagram.
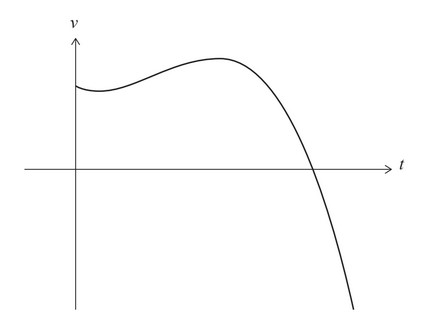
At t = 0, the object is at the origin.
(a) Find the displacement of the object from the origin at t = 1.
(b) Find an expression for the acceleration of the object.
(c) Hence, find the greatest speed reached by the object before it comes to rest.
(d) Find the greatest speed reached by the object for 0 ≤ t ≤ 4 .
(e) Write down an expression that represents the distance travelled by the object while its speed is increasing. Do not evaluate the expression.
Answer/Explanation
Answer:
(a) attempt to integrate v (integration of at least one term)
\((s(t)=) – \frac{1}{4}t^4 + \frac{7}{6}t^3 – t^2 + 6t (+C)\)
substitution of t = 1 into their integrated expression
displacement = \(5\frac{11}{12}(=\frac{71}{12})(m)\)
(b) attempt to differentiate v (differentiation of at least one term)
\(a(t) = -3t^2 + 7t – 2\)
(c) setting their v'(t) = 0
\(-3t^2 + 7t – 2 =0\)
valid attempt to solve quadratic
(3t – 1)(t – 2) = 0 OR \(\frac{-7 \neq \sqrt{49-4(-3)(-2)}}{-6}\)
\(t = \frac{1}{3}\), 2 (t = \(\frac{1}{3}\) may be omitted)
substitute their largest positive t-value into v(t)
greatest speed is 8 \(ms^{-1}\)
(d) attempt to check other boundary value at t = 4
v(4) = -64 + 56 – 8 + 6 (=-10)
greatest speed is 10 \(ms^{-1}\)
(e) identifying correct intervals where speed increases (may be seen in integral)
\(t = \frac{1}{3}\) to t = 2 and t = k to t = 4
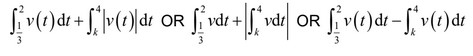
Question
In this question, all lengths are in metres and time is in seconds.
Consider two particles, P1 and P2 , which start to move at the same time.
Particle P1 moves in a straight line such that its displacement from a fixed-point is given by s (t) = 10 – \(\frac{7}{4}\) t2 , for t ≥ 0 .
Find an expression for the velocity of P1 at time t . [2]
Particle P2 also moves in a straight line. The position of P2 is given by
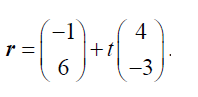
The speed of P1 is greater than the speed of P2 when t > q .
Find the value of q . [5]
Answer/Explanation
Ans:
(a)
recognizing velocity is derivative of displacement
eg v= \(\frac{ds}{dt},\frac{d}{dt}(10-\frac{7}{4}t^{2})\)
velocity = -\(\frac{14}{4}t (=-\frac{7}{2}t)\)
(b)
valid approach to find speed of P2
\(|(_{-3}^{4})|, \sqrt{4^{2}+(-3)^{2}}\), volocity = \(\sqrt{4^{2}+(-3)^{2}}\)
correct speed
eg \(5ms ^{-1}\)
recognizing relationship between speed and velocity (may be seen in inequality/equation)
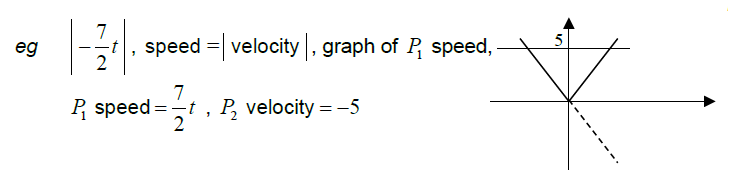
correct inequality or equation that compares speed or velocity (accept any variable for q)
eg \(|-\frac{7}{2}t|>5,-\frac{7}{2}q<-5 , \frac{7}{2}q> 5,\frac{7}{2}q= 5\)
\(q= \frac{10}{7}\)(seconds)(accept t \(> \frac{10}{7})\), do not accept \(t = \frac{10}{7}\)
Question
A particle moves along a straight line so that its velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\)at time t seconds is given by \(v = 6{{\rm{e}}^{3t}} + 4\) . When \(t = 0\) , the displacement, s, of the particle is 7 metres. Find an expression for s in terms of t.
Answer/Explanation
Markscheme
evidence of anti-differentiation (M1)
e.g. \(s = \int {(6{{\rm{e}}^{3x}} + 4)} {\rm{d}}x\)
\(s = 2{{\rm{e}}^{3t}} + 4t + C\) A2A1
substituting \(t = 0\) , (M1)
\(7 = 2 + C\) A1
\(C = 5\)
\(s = 2{{\rm{e}}^{3t}} + 4t + 5\) A1 N3
[7 marks]