Download IITian Academy App for accessing Online Mock Tests and More..
Question
The acceleration, \(a{\text{ m}}{{\text{s}}^{ – 2}}\), of a particle at time t seconds is given by \[a = \frac{1}{t} + 3\sin 2t {\text{, for }} t \ge 1.\]
The particle is at rest when \(t = 1\) .
Find the velocity of the particle when \(t = 5\) .
Answer/Explanation
Markscheme
evidence of integrating the acceleration function (M1)
e.g. \(\int {\left( {\frac{1}{t} + 3\sin 2t} \right)} {\rm{d}}t\)
correct expression \(\ln t – \frac{3}{2}\cos 2t + c\) A1A1
evidence of substituting (1, 0) (M1)
e.g. \(0 = \ln 1 – \frac{3}{2}\cos 2 + c\)
\(c = – 0.624\) \(\left( { = \frac{3}{2}\cos 2 – \ln {\text{1 or }}\frac{{\rm{3}}}{{\rm{2}}}\cos 2} \right)\) (A1)
\(v = \ln t – \frac{3}{2}\cos 2t – 0.624\) \(\left( { = \ln t – \frac{3}{2}\cos 2t + \frac{3}{2}\cos {\text{2 or ln}}t – \frac{3}{2}\cos 2t + \frac{3}{2}\cos 2 – \ln 1} \right)\) (A1)
\(v(5) = 2.24\) (accept the exact answer \(\ln 5 – 1.5\cos 10 + 1.5\cos 2\) ) A1 N3
[7 marks]
Question
A particle moves in a straight line with velocity \(v = 12t – 2{t^3} – 1\) , for \(t \ge 0\) , where v is in centimetres per second and t is in seconds.
Find the acceleration of the particle after 2.7 seconds.
Find the displacement of the particle after 1.3 seconds.
Answer/Explanation
Markscheme
recognizing that acceleration is the derivative of velocity (seen anywhere) (R1)
e.g. \(a = \frac{{{{\rm{d}}^2}s}}{{{\rm{d}}{t^2}}},v’,12 – 6{t^2}\)
correctly substituting 2.7 into their expression for a (not into v) (A1)
e.g. \(s”(2.7)\)
\({\text{acceleration}} = – 31.74\) (exact), \( – 31.7\) A1 N3
[3 marks]
recognizing that displacement is the integral of velocity R1
e.g. \(s = \int v \)
correctly substituting 1.3 (A1)
e.g. \(\int_0^{1.3} {v{\rm{d}}t} \)
\({\text{displacement}} = 7.41195\) (exact), \(7.41\) (cm) A1 N2
[3 marks]
Question
A particle’s displacement, in metres, is given by \(s(t) = 2t\cos t\) , for \(0 \le t \le 6\) , where t is the time in seconds.
On the grid below, sketch the graph of \(s\) .
Find the maximum velocity of the particle.
Answer/Explanation
Markscheme
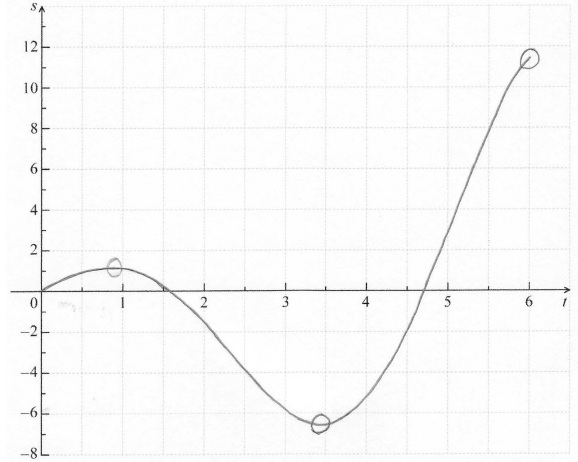A1A1A1A1 N4
Note: Award A1 for approximately correct shape (do not accept line segments).
Only if this A1 is awarded, award the following:
A1 for maximum and minimum within circles,
A1 for x-intercepts between 1 and 2 and between 4 and 5,
A1 for left endpoint at \((0{\text{, }}0)\) and right endpoint within circle.
[4 marks]
appropriate approach (M1)
e.g. recognizing that \(v = s’\) , finding derivative, \(a = s”\)
valid method to find maximum (M1)
e.g. sketch of \(v\) , \(v'(t) = 0\) , \(t = 5.08698 \ldots \)
\(v = 10.20025 \ldots \)
\(v = 10.2\) \([10.2{\text{, }}10.3]\) A1 N2
[3 marks]
Question
A particle moves along a straight line such that its velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\), is given by \(v(t) = 10t{{\text{e}}^{ – 1.7t}}\), for \(t \geqslant 0\).
On the grid below, sketch the graph of \(v\), for \(0 \leqslant t \leqslant 4\).
Find the distance travelled by the particle in the first three seconds.
Find the velocity of the particle when its acceleration is zero.
Answer/Explanation
Markscheme
A1A2 N3
Notes: Award A1 for approximately correct domain \(0 \leqslant t \leqslant 4\).
The shape must be approximately correct, with maximum skewed left. Only if the shape is approximately correct, award A2 for all the following approximately correct features, in circle of tolerance where drawn (accept seeing correct coordinates for the maximum, even if point outside circle):
Maximum point, passes through origin, asymptotic to \(t\)-axis (but must not touch the axis).
If only two of these features are correct, award A1.
[3 marks]
valid approach (including \(0\) and \(3\)) (M1)
eg \(\int_0^3 {10t{{\text{e}}^{ – 1.7t}}{\text{d}}t,{\text{ }}\int_0^3 {f(x)} } \), area from \(0\) to \(3\) (may be shaded in diagram)
\({\text{distance}} = 3.33{\text{ (m)}}\) A1 N2
[2 marks]
recognizing acceleration is derivative of velocity (R1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), attempt to find \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\), reference to maximum on the graph of \(v\)
valid approach to find \(v\) when \(a = 0\) (may be seen on graph) (M1)
eg \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = 0,{\text{ }}10{{\text{e}}^{ – 1.7t}} – 17t{{\text{e}}^{ – 1.7t}} = 0,{\text{ }}t = 0.588\)
\({\text{velocity}} = 2.16{\text{ (m}}{{\text{s}}^{ – 1}})\) A1 N3
Note: Award R1M1A0 for \((0.588, 216)\) if velocity is not identified as final answer
[3 marks]
Question
Ramiro and Lautaro are travelling from Buenos Aires to El Moro.
Ramiro travels in a vehicle whose velocity in \({\text{m}}{{\text{s}}^{ – 1}}\) is given by \({V_R} = 40 – {t^2}\), where \(t\) is in seconds.
Lautaro travels in a vehicle whose displacement from Buenos Aires in metres is given by \({S_L} = 2{t^2} + 60\).
When \(t = 0\), both vehicles are at the same point.
Find Ramiro’s displacement from Buenos Aires when \(t = 10\).
Answer/Explanation
Markscheme
METHOD 1
\({S_L}(0) = 60\) (seen anywhere) (A1)
recognizing need to integrate \({V_R}\) (M1)
eg \({S_R}(t)\int {{V_R}{\text{d}}t} \)
correct expression A1A1
eg \(40t – \frac{1}{3}{t^3} + C\)
Note: Award A1 for \(40t\), and A1 for \( – \frac{1}{3}{t^3}\).
equate displacements to find C (R1)
eg \(40(0) – \frac{1}{3}{(0)^3} + C = 60,{\text{ }}{S_L}(0) = {S_R}(0)\)
\(C = 60\) A1
attempt to find displacement (M1)
eg \({S_R}(10),{\text{ }}40(10) – \frac{1}{3}{(10)^3} + 60\)
\(126.666\)
\(126\frac{2}{3}{\text{ (exact), 127 (m)}}\) A1 N5
METHOD 2
recognizing need to integrate \({V_R}\) (M1)
eg \({S_R}(t) = \int {{V_R}{\text{d}}t} \)
valid approach involving a definite integral (M1)
eg \(\int_a^b {{V_R}{\text{d}}t} \)
correct expression with limits (A1)
eg \(\int_0^{10} {\left( {40 – {t^2}} \right){\text{d}}t,{\text{ }}} \int_0^{10} {{V_R}{\text{d}}t,{\text{ }}\left[ {40t – \frac{1}{3}{t^3}} \right]} _0^{10}\)
\(66.6666\) A2
\({S_L}(0) = 60\) (seen anywhere) (A1)
valid approach to find total displacement (M1)
eg \(60 + 66.666\)
\(126.666\)
\(126\frac{2}{3}\) (exact), \(127\) (m) A1 N5
METHOD 3
\({S_L}(0) = 60\) (seen anywhere) (A1)
recognizing need to integrate \({V_R}\) (M1)
eg \({S_R}(t) = \int {{V_R}{\text{d}}t} \)
correct expression A1A1
eg \(40t – \frac{1}{3}{t^3} + C\)
Note: Award A1 for \(40t\), and A1 for \( – \frac{1}{3}{t^3}\).
correct expression for Ramiro displacement A1
eg \({S_R}(10) – {S_R}(0),{\text{ }}\left[ {40t – \frac{1}{3}{t^3} + C} \right]_0^{10}\)
\(66.6666\) A1
valid approach to find total displacement (M1)
eg \(60 + 66.6666\)
\(126\frac{2}{3}\) (exact), 127 (m) A1 N5
[8 marks]
Question
A particle moves in a straight line. Its velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\), at time \(t\) seconds, is given by
\[v = {\left( {{t^2} – 4} \right)^3},{\text{ for }}0 \leqslant t \leqslant 3.\]
Find the velocity of the particle when \(t = 1\).
Find the value of \(t\) for which the particle is at rest.
Find the total distance the particle travels during the first three seconds.
Show that the acceleration of the particle is given by \(a = 6t{({t^2} – 4)^2}\).
Find all possible values of \(t\) for which the velocity and acceleration are both positive or both negative.
Answer/Explanation
Markscheme
substituting \(t = 1\) into \(v\) (M1)
eg \(v(1),{\text{ }}{\left( {{1^2} – 4} \right)^3}\)
velocity \( = – 27{\text{ }}\left( {{\text{m}}{{\text{s}}^{ – 1}}} \right)\) A1 N2
[2 marks]
valid reasoning (R1)
eg \(v = 0,{\text{ }}{\left( {{t^2} – 4} \right)^3} = 0\)
correct working (A1)
eg \({t^2} – 4 = 0,{\text{ }}t = \pm 2\), sketch
\(t = 2\) A1 N2
[3 marks]
correct integral expression for distance (A1)
eg \(\int_0^3 {\left| v \right|,{\text{ }}\int {\left| {{{\left( {{t^2} – 4} \right)}^3}} \right|,{\text{ }} – \int_0^2 {v{\text{d}}t + \int_2^3 {v{\text{d}}t} } } } \),
\(\int_0^2 {{{\left( {4 – {t^2}} \right)}^3}{\text{d}}t + \int_2^3 {{{\left( {{t^2} – 4} \right)}^3}{\text{d}}t} }\) (do not accept \(\int_0^3 {v{\text{d}}t} \))
\(86.2571\)
\({\text{distance}} = 86.3{\text{ (m)}}\) A2 N3
[3 marks]
evidence of differentiating velocity (M1)
eg \(v'(t)\)
\(a = 3{\left( {{t^2} – 4} \right)^2}(2t)\) A2
\(a = 6t{\left( {{t^2} – 4} \right)^2}\) AG N0
[3 marks]
METHOD 1
valid approach M1
eg graphs of \(v\) and \(a\)
correct working (A1)
eg areas of same sign indicated on graph
\(2 < t \leqslant 3\) (accept \(t > 2\)) A2 N2
METHOD 2
recognizing that \(a \geqslant 0\) (accept \(a\) is always positive) (seen anywhere) R1
recognizing that \(v\) is positive when \(t > 2\) (seen anywhere) (R1)
\(2 < t \leqslant 3\) (accept \(t > 2\)) A2 N2
[4 marks]
Question
A particle starts from point \(A\) and moves along a straight line. Its velocity, \(v\;{\text{m}}{{\text{s}}^{ – 1}}\), after \(t\) seconds is given by \(v(t) = {{\text{e}}^{\frac{1}{2}\cos t}} – 1\), for \(0 \le t \le 4\). The particle is at rest when \(t = \frac{\pi }{2}\).
The following diagram shows the graph of \(v\).
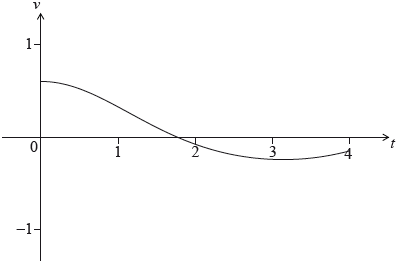
Find the distance travelled by the particle for \(0 \le t \le\ \frac{\pi }{2}\).
Explain why the particle passes through \(A\) again.
Answer/Explanation
Markscheme
correct substitution of function and/or limits into formula (A1)
(accept absence of d\(t\), but do not accept any errors)
eg\(\;\;\;\)\(\int_0^{\frac{\pi }{2}} {v,{\text{ }}\int {\left| {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right|{\text{d}}t,{\text{ }}\int {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right)} } } \)
\(0.613747\)
distance is \(0.614{\text{ }}[0.613,{\text{ }}0.614]{\text{ (m)}}\) A1 N2
[2 marks]
METHOD 1
valid attempt to find the distance travelled between \(t = \frac{\pi }{2}\) and \(t = 4\) (M1)
eg\(\;\;\;\)\(\int_{\frac{\pi }{2}}^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right),{\text{ }}\int_0^4 {\left| {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right|{\text{d}}t – 0.614} } \)
distance is \(0.719565\) A1
valid reason, referring to change of direction (may be seen in explanation) R1
valid explanation comparing their distances R1
eg\(\;\;\;\)\(0.719565 > 0.614\), distance moving back is more than distance moving forward
Note: Do not award the final R1 unless the A1 is awarded.
particle passes through \(A\) again AG N0
METHOD 2
valid attempt to find displacement (M1)
eg\(\;\;\;\)\(\int_{\frac{\pi }{2}}^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right),{\text{ }}\int_0^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} – 1} \right)} } \)
correct displacement A1
eg\(\;\;\;\)\(-0.719565,{\text{ }}-0.105817\)
recognizing that displacement from \(0\) to \(\frac{\pi }{2}\) is positive R1
eg\(\;\;\;\)displacement = distance from \(0\) to \(\frac{\pi }{2}\)
valid explanation referring to positive and negative displacement R1
eg\(\;\;\;\)\(0.719565 > 0.614\), overall displacement is negative, since displacement after \(\frac{\pi }{2}\) is negative, then particle gone backwards more than forwards
Note: Do not award the final R1 unless the A1 and the first R1 are awarded.
particle passes through A\(A\) again AG N0
[4 marks]
Note: Special Case.
If all working shown, and candidates seem to have misread the question, using [equation], award marks as follows:
(a) correct substitution of function and/or limits into formula (accept absence of dt, but do not accept any errors) A0MR
eg [equation]
\(2.184544\)
distance is \(2.18\) [\(2.18\), \(2.19\)] (m) A1 N0
(b) METHOD 1
valid attempt to find the distance travelled between [equation] M1
eg [equation]
distance is \(1.709638\) A1
reference to change of direction (may be seen in explanation) R1
reasoning/stating particle passes/does not pass through \(A\) again R0
METHOD 2
valid attempt to find displacement M1
eg [equation]
correct displacement A1
eg \(1.709638,{\rm{ }}3.894182\)
recognising that displacement from [ \(0\) to (pi/2] is positive R0
reasoning/stating particle passes/does not pass through \(A\) again R0
With method 2, there is no valid reasoning about whether the particle passes through \(A\) again or not, so they cannot gain the R marks.
Total [6 marks]
Question
The velocity \(v{\text{ m}}{{\text{s}}^{ – 1}}\) of a particle after \(t\) seconds is given by
\(v(t) = {(0.3t + 0.1)^t} – 4\), for \(0 \le t \le 5\)
The following diagram shows the graph of \(v\).
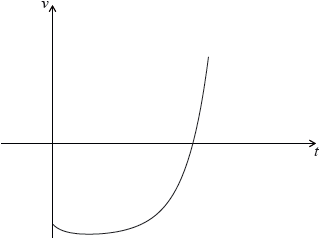
Find the value of \(t\) when the particle is at rest.
Find the value of \(t\) when the acceleration of the particle is \(0\).
Answer/Explanation
Markscheme
recognizing particle at rest when \(v = 0\) (M1)
eg\(\;\;\;{(0.3t + 0.1)^t} – 4 = 0\), \(x\)-intercept on graph of \(v\)
\(t = 4.27631\)
\(t = 4.28{\text{ }} {\text{ (seconds)}}\) A2 N3
[3 marks]
valid approach to find \(t\) when \(a\) is \(0\) (M1)
eg\(\;\;\;v'(t) = 0\), \(v\) minimum
\(t = 1.19236\)
\(t = 1.19{\text{ }}{\text{ (seconds)}}\) A2 N3
[3 marks]
Total [6 marks]
Question
A particle P moves along a straight line so that its velocity, \(v\,{\text{m}}{{\text{s}}^{ – 1}}\), after \(t\) seconds, is given by \(v = \cos 3t – 2\sin t – 0.5\), for \(0 \leqslant t \leqslant 5\). The initial displacement of P from a fixed point O is 4 metres.
The following sketch shows the graph of \(v\).
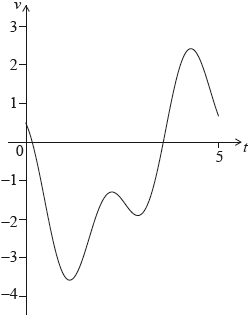
Find the displacement of P from O after 5 seconds.
Find when P is first at rest.
Write down the number of times P changes direction.
Find the acceleration of P after 3 seconds.
Find the maximum speed of P.
Answer/Explanation
Markscheme
METHOD 1
recognizing \(s = \int v \) (M1)
recognizing displacement of P in first 5 seconds (seen anywhere) A1
(accept missing \({\text{d}}t\))
eg\(\,\,\,\,\,\)\(\int_0^5 {v{\text{d}}t,{\text{ }} – 3.71591} \)
valid approach to find total displacement (M1)
eg\(\,\,\,\,\,\)\(4 + ( – 3.7159),{\text{ }}s = 4 + \int_0^5 v \)
0.284086
0.284 (m) A2 N3
METHOD 2
recognizing \(s = \int v \) (M1)
correct integration A1
eg\(\,\,\,\,\,\)\(\frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c\) (do not penalize missing “\(c\)”)
attempt to find \(c\) (M1)
eg\(\,\,\,\,\,\)\(4 = \frac{1}{3}\sin (0) + 2\cos (0)–\frac{0}{2} + c,{\text{ }}4 = \frac{1}{3}\sin 3t + 2\cos t – \frac{t}{2} + c,{\text{ }}2 + c = 4\)
attempt to substitute \(t = 5\) into their expression with \(c\) (M1)
eg\(\,\,\,\,\,\)\(s(5),{\text{ }}\frac{1}{3}\sin (15) + 2\cos (5)5–\frac{5}{2} + 2\)
0.284086
0.284 (m) A1 N3
[5 marks]
recognizing that at rest, \(v = 0\) (M1)
\(t = 0.179900\)
\(t = 0.180{\text{ (secs)}}\) A1 N2
[2 marks]
recognizing when change of direction occurs (M1)
eg\(\,\,\,\,\,\)\(v\) crosses \(t\) axis
2 (times) A1 N2
[2 marks]
acceleration is \({v’}\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(v'(3)\)
0.743631
\(0.744{\text{ }}({\text{m}}{{\text{s}}^{ – 2}})\) A1 N2
[2 marks]
valid approach involving max or min of \(v\) (M1)
eg\(\,\,\,\,\,\)\(v\prime = 0,{\text{ }}a = 0\), graph
one correct co-ordinate for min (A1)
eg\(\,\,\,\,\,\)\(1.14102,{\text{ }}-3.27876\)
\(3.28{\text{ }}({\text{m}}{{\text{s}}^{ – 1}})\) A1 N2
[3 marks]
Question
A particle moves in a straight line. Its velocity \(v{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v = 6t – 6,{\text{ for }}0 \leqslant t \leqslant 2.\]
After \(p\) seconds, the particle is 2 m from its initial position. Find the possible values of \(p\).
Answer/Explanation
Markscheme
correct approach (A1)
eg\(\,\,\,\,\,\)\(s = \int {v,{\text{ }}\int_0^p {6t – 6{\text{d}}t} } \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\int {6t – 6{\text{d}}t = 3{t^2} – 6t + C,{\text{ }}\left[ {3{t^2} – 6t} \right]_0^p} \)
recognizing that there are two possibilities (M1)
eg\(\,\,\,\,\,\)2 correct answers, \(s = \pm 2,{\text{ }}c \pm 2\)
two correct equations in \(p\) A1A1
eg\(\,\,\,\,\,\)\(3{p^2} – 6p = 2,{\text{ }}3{p^2} – 6p = – 2\)
0.42265, 1.57735
\(p = 0.423{\text{ or }}p = 1.58\) A1A1 N3
[7 marks]
Question
A particle P starts from a point A and moves along a horizontal straight line. Its velocity \(v{\text{ cm}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by
\[v(t) = \left\{ {\begin{array}{*{20}{l}} { – 2t + 2,}&{{\text{for }}0 \leqslant t \leqslant 1} \\ {3\sqrt t + \frac{4}{{{t^2}}} – 7,}&{{\text{for }}1 \leqslant t \leqslant 12} \end{array}} \right.\]
The following diagram shows the graph of \(v\).
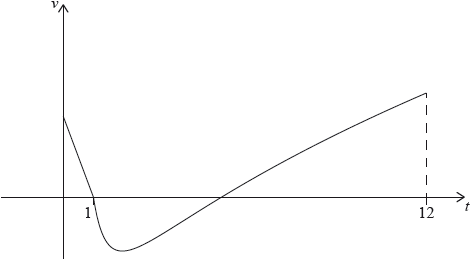
P is at rest when \(t = 1\) and \(t = p\).
When \(t = q\), the acceleration of P is zero.
Find the initial velocity of \(P\).
Find the value of \(p\).
(i) Find the value of \(q\).
(ii) Hence, find the speed of P when \(t = q\).
(i) Find the total distance travelled by P between \(t = 1\) and \(t = p\).
(ii) Hence or otherwise, find the displacement of P from A when \(t = p\).
Answer/Explanation
Markscheme
valid attempt to substitute \(t = 0\) into the correct function (M1)
eg\(\,\,\,\,\,\)\( – 2(0) + 2\)
2 A1 N2
[2 marks]
recognizing \(v = 0\) when P is at rest (M1)
5.21834
\(p = 5.22{\text{ }}({\text{seconds}})\) A1 N2
[2 marks]
(i) recognizing that \(a = v’\) (M1)
eg\(\,\,\,\,\,\)\(v’ = 0\), minimum on graph
1.95343
\(q = 1.95\) A1 N2
(ii) valid approach to find their minimum (M1)
eg\(\,\,\,\,\,\)\(v(q),{\text{ }} – 1.75879\), reference to min on graph
1.75879
speed \( = 1.76{\text{ }}(c\,{\text{m}}\,{{\text{s}}^{ – 1}})\) A1 N2
[4 marks]
(i) substitution of correct \(v(t)\) into distance formula, (A1)
eg\(\,\,\,\,\,\)\(\int_1^p {\left| {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right|{\text{d}}t,{\text{ }}\left| {\int {3\sqrt t + \frac{4}{{{t^2}}} – 7{\text{d}}t} } \right|} \)
4.45368
distance \( = 4.45{\text{ }}({\text{cm}})\) A1 N2
(ii) displacement from \(t = 1\) to \(t = p\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\( – 4.45368,{\text{ }}\int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t} \)
displacement from \(t = 0\) to \(t = 1\) (A1)
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t,{\text{ }}0.5 \times 1 \times 2,{\text{ 1}}} \)
valid approach to find displacement for \(0 \leqslant t \leqslant p\) M1
eg\(\,\,\,\,\,\)\(\int_0^1 {( – 2t + 2){\text{d}}t + \int_1^p {\left( {3\sqrt t + \frac{4}{{{t^2}}} – 7} \right){\text{d}}t,{\text{ }}\int_0^1 {( – 2t + 2){\text{d}}t – 4.45} } } \)
\( – 3.45368\)
displacement \( = – 3.45{\text{ }}({\text{cm}})\) A1 N2
[6 marks]
Question
Note: In this question, distance is in metres and time is in seconds.
A particle P moves in a straight line for five seconds. Its acceleration at time \(t\) is given by \(a = 3{t^2} – 14t + 8\), for \(0 \leqslant t \leqslant 5\).
When \(t = 0\), the velocity of P is \(3{\text{ m}}\,{{\text{s}}^{ – 1}}\).
Write down the values of \(t\) when \(a = 0\).
Hence or otherwise, find all possible values of \(t\) for which the velocity of P is decreasing.
Find an expression for the velocity of P at time \(t\).
Find the total distance travelled by P when its velocity is increasing.
Answer/Explanation
Markscheme
\(t = \frac{2}{3}{\text{ (exact), }}0.667,{\text{ }}t = 4\) A1A1 N2
[2 marks]
recognizing that \(v\) is decreasing when \(a\) is negative (M1)
eg\(\,\,\,\,\,\)\(a < 0,{\text{ }}3{t^2} – 14t + 8 \leqslant 0\), sketch of \(a\)
correct interval A1 N2
eg\(\,\,\,\,\,\)\(\frac{2}{3} < t < 4\)
[2 marks]
valid approach (do not accept a definite integral) (M1)
eg\(\,\,\,\,\,\)\(v\int a \)
correct integration (accept missing \(c\)) (A1)(A1)(A1)
\({t^3} – 7{t^2} + 8t + c\)
substituting \(t = 0,{\text{ }}v = 3\) , (must have \(c\)) (M1)
eg\(\,\,\,\,\,\)\(3 = {0^3} – 7({0^2}) + 8(0) + c,{\text{ }}c = 3\)
\(v = {t^3} – 7{t^2} + 8t + 3\) A1 N6
[6 marks]
recognizing that \(v\) increases outside the interval found in part (b) (M1)
eg\(\,\,\,\,\,\)\(0 < t < \frac{2}{3},{\text{ }}4 < t < 5\), diagram
one correct substitution into distance formula (A1)
eg\(\,\,\,\,\,\)\(\int_0^{\frac{2}{3}} {\left| v \right|,{\text{ }}\int_4^5 {\left| v \right|} ,{\text{ }}\int_{\frac{2}{3}}^4 {\left| v \right|} ,{\text{ }}\int_0^5 {\left| v \right|} } \)
one correct pair (A1)
eg\(\,\,\,\,\,\)3.13580 and 11.0833, 20.9906 and 35.2097
14.2191 A1 N2
\(d = 14.2{\text{ (m)}}\)
[4 marks]
Question
Let \(f\left( x \right) = 12\,\,{\text{cos}}\,x – 5\,\,{\text{sin}}\,x,\,\, – \pi \leqslant x \leqslant 2\pi \), be a periodic function with \(f\left( x \right) = f\left( {x + 2\pi } \right)\)
The following diagram shows the graph of \(f\).
There is a maximum point at A. The minimum value of \(f\) is −13 .
A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.
The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by
\(d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.\)
Find the coordinates of A.
For the graph of \(f\), write down the amplitude.
For the graph of \(f\), write down the period.
Hence, write \(f\left( x \right)\) in the form \(p\,\,{\text{cos}}\,\left( {x + r} \right)\).
Find the maximum speed of the ball.
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
Answer/Explanation
Markscheme
−0.394791,13
A(−0.395, 13) A1A1 N2
[2 marks]
13 A1 N1
[1 mark]
\({2\pi }\), 6.28 A1 N1
[1 mark]
valid approach (M1)
eg recognizing that amplitude is p or shift is r
\(f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)\) (accept p = 13, r = 0.395) A1A1 N3
Note: Accept any value of r of the form \(0.395 + 2\pi k,\,\,k \in \mathbb{Z}\)
[3 marks]
recognizing need for d ′(t) (M1)
eg −12 sin(t) − 5 cos(t)
correct approach (accept any variable for t) (A1)
eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32
maximum speed = 13 (cms−1) A1 N2
[3 marks]
recognizing that acceleration is needed (M1)
eg a(t), d ”(t)
correct equation (accept any variable for t) (A1)
eg \(a\left( t \right) = – 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d’\left( t \right)} \right)} \right| = 2,\,\, – 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = – 2\)
valid attempt to solve their equation (M1)
eg sketch, 1.33
1.02154
1.02 A2 N3
[5 marks]
Question
A particle P moves along a straight line. The velocity v m s−1 of P after t seconds is given by v (t) = 7 cos t − 5t cos t, for 0 ≤ t ≤ 7.
The following diagram shows the graph of v.
Find the initial velocity of P.
Find the maximum speed of P.
Write down the number of times that the acceleration of P is 0 m s−2 .
Find the acceleration of P when it changes direction.
Find the total distance travelled by P.
Answer/Explanation
Markscheme
initial velocity when t = 0 (M1)
eg v(0)
v = 17 (m s−1) A1 N2
[2 marks]
recognizing maximum speed when \(\left| v \right|\) is greatest (M1)
eg minimum, maximum, v’ = 0
one correct coordinate for minimum (A1)
eg 6.37896, −24.6571
24.7 (ms−1) A1 N2
[3 marks]
recognizing a = v ′ (M1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), correct derivative of first term
identifying when a = 0 (M1)
eg turning points of v, t-intercepts of v ′
3 A1 N3
[3 marks]
recognizing P changes direction when v = 0 (M1)
t = 0.863851 (A1)
−9.24689
a = −9.25 (ms−2) A2 N3
[4 marks]
correct substitution of limits or function into formula (A1)
eg \(\int_0^7 {\left| {\,v\,} \right|,\,\int_0^{0.8638} {v{\text{d}}t – \int_{0.8638}^7 {v{\text{d}}t} } ,\,\,\int {\left| {\,7\,{\text{cos}}\,x – 5{x^{{\text{cos}}\,x}}\,} \right|} \,dx,\,\,3.32 = 60.6} \)
63.8874
63.9 (metres) A2 N3
[3 marks]