IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 10.2 Fields at work
Topic 10 Weightage : 5 %
All Questions for Topic 10.2 – Potential and potential energy , Potential gradient , Potential difference , Escape speed , Orbital motion, orbital speed and orbital energy , Forces and inverse-square law behaviour
Question
The diagram shows the electric field lines of a positively charged conducting sphere of radius
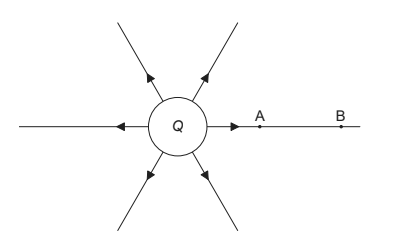
Points A and B are located on the same field line.
A proton is placed at A and released from rest. The magnitude of the work done by the electric field in moving the proton from A to B is 1.7 × 10–16 J.
Point A is at a distance of 5.0 × 10–2 m from the centre of the sphere. Point B is at a distance of 1.0 × 10–1 m from the centre of the sphere.
(i) Calculate the electric potential difference between points A and B. [1]
(ii) Determine the charge Q of the sphere. [2]
▶️Answer/Explanation
Ans
i « \(\frac{W}{P}\) = \(\frac{1.7\times 10^{-16}}{1.60\times10 ^{-19}}\)= » 1.1 × 103
ii.
\(8.99\times10^9\times Q \times (\frac{1}{5.0\times 10^{-2}}-\frac{1}{1.0\times 10^{-1}})=1.1\times 10^3\)
Q =1.2 × 10-8 «C»
This question is about a probe in orbit.
A probe of mass m is in a circular orbit of radius r around a spherical planet of mass M.
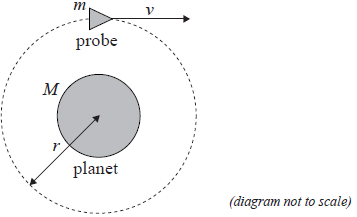
a. State why the work done by the gravitational force during one full revolution of the probe is zero.[1]
(i) speed is \(v = \sqrt {\frac{{GM}}{r}} \).
(ii) total energy is \(E = – \frac{{GMm}}{{2r}}\). [4]
State and explain whether the work done on the probe by the engines is positive, negative or zero. [2]
▶️Answer/Explanation
Markscheme
a.
because the force is always at right angles to the velocity / motion/orbit is an equipotential surface;
Do not accept answers based on the displacement being zero for a full revolution.
(i) equating gravitational force \(\frac{{GMm}}{{{r^2}}}\);
to centripetal force \(\frac{{m{v^2}}}{r}\) to get result;
(ii) kinetic energy is \(\frac{{GMm}}{{2r}}\);
addition to potential energy −\(\frac{{GMm}}{{r}}\) to get result;
the total energy (at the new orbit) will be greater than before/is less negative;
hence probe engines must be fired to produce force in the direction of motion / positive work must be done (on the probe);
Award [1] for mention of only potential energy increasing.
This question is in two parts. Part 1 is about collisions. Part 2 is about the gravitational field of Mars.
Part 1 Collisions
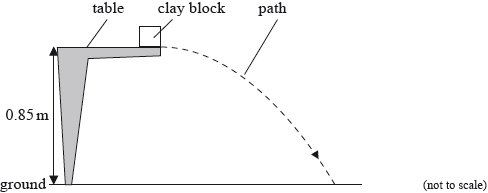
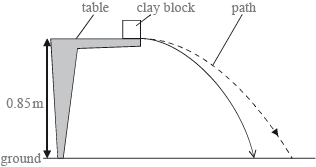
The experiment is repeated with the clay block placed at the edge of the table so that it is fired away from the table. The initial speed of the clay block is \({\text{4.3 m}}\,{{\text{s}}^{ – 1}}\) horizontally. The table surface is 0.85 m above the ground.
Part 2 Gravitational field of Mars
The graph shows the variation with distance \(r\) from the centre of Mars of the gravitational potential \(V\). \(R\) is the radius of Mars which is 3.3 Mm. (Values of \(V\) for \(r < R\) are not shown.)
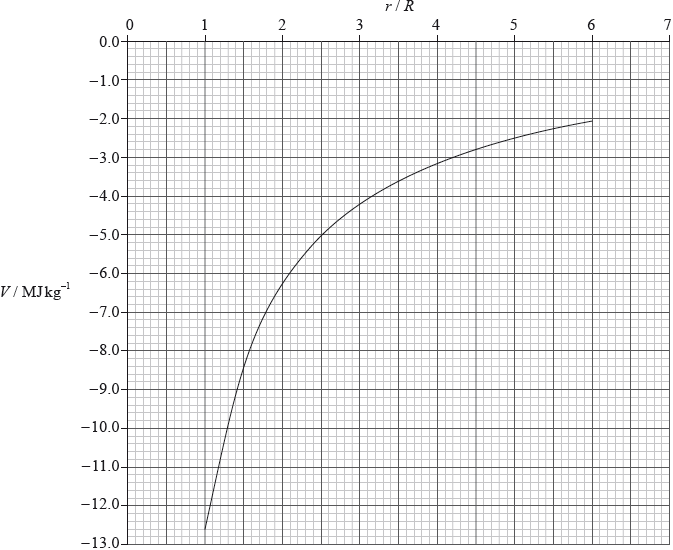
A rocket of mass \(1.2 \times {10^4}{\text{ kg}}\) lifts off from the surface of Mars. Use the graph to
Part1.c.
(i) Ignoring air resistance, calculate the horizontal distance travelled by the clay block before it strikes the ground.
(ii) The diagram in (c) shows the path of the clay block neglecting air resistance. On the diagram, draw the approximate shape of the path that the clay block will take assuming that air resistance acts on the clay block. [7]
Define gravitational potential energy of a mass at a point. [1]
(i) calculate the change in gravitational potential energy of the rocket at a distance 4R from the centre of Mars.
(ii) show that the magnitude of the gravitational field strength at a distance 4R from the centre of Mars is \({\text{0.23 N}}\,{\text{k}}{{\text{g}}^{ – 1}}\). [5]
▶️Answer/Explanation
Markscheme
Part1.c.
(i) use of kinematic equation to yield time;
\(t = \sqrt {\frac{{2s}}{g}} {\text{ (}} = 0.42{\text{ s)}}\);
\(s = {\text{horizontal speed\( \times \)time}}\);
\( = 1.8{\text{ m}}\);
Accept g = 10 m\(\,\)s\(^{ – 2}\) equivalent answers 1.79 from 9.8, 1.77 from 10.
(ii) initial drawn velocity horizontal; (judge by eye)
reasonable shape; (i.e. quasi-parabolic)
horizontal distance moved always decreasing when compared to given path / range less than original;
work done in moving mass from infinity to a point;
(i) read offs \( – 12.6\) and \( – 3.2\);
gain in \({\text{gpe }}1.2 \times {10^4} \times [12.6 – 3.2]\) or gain in g potential \(\left[ {12.6 \times {{10}^6} – 3.2 \times {{10}^6}} \right]\);
\( = 1.13 \pm 0.05 \times {10^5}{\text{ MJ}}\) or \(1.13 \pm 0.05 \times {10^{11}}{\text{ J}}\);
(ii) use of gradient of graph to determine \(g\);
values substituted from drawn gradient \(\left( {{\text{typically }}\frac{{6.7 \times {{10}^6}}}{{7 \times 3.3 \times {{10}^6}}}} \right)\);
\( = 0.23{\text{ N}}\,{\text{k}}{{\text{g}}^{ – 1}}\) (allow answers in the range of 0.20 to 0.26 N\(\,\)kg–1)
Award [0] for solutions from \(\frac{V}{r}\).
Part1.c.
(i) Candidates were required to determine the time taken to fall to the floor and then use this time to evaluate the distance travelled horizontally. Many managed this with more or less success.
(ii) Many candidates produced poor attempts at the sketch. Initial trajectories were not horizontal and the general shapes of the curves were usually not quasi-parabolic.
Some candidates gave a definition of gravitational potential, i.e. they related the energy to that of a unit mass.
Throughout this part candidates were instructed to use the graph, those who used other non-graphical methods were penalised.
(i) There were many good evaluations with complete and well presented solutions.
(ii) Use of the Data Booklet equation for gravitational field strength without reference to the graph was common.
