IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 11.2 Power generation and transmission
Topic 11 Weightage : 5 %
All Questions for Topic 11.2 – Alternating current (ac) generators , Average power and root mean square (rms) values of current and voltage , Transformers , Diode bridges , Half-wave and full-wave rectification
Question
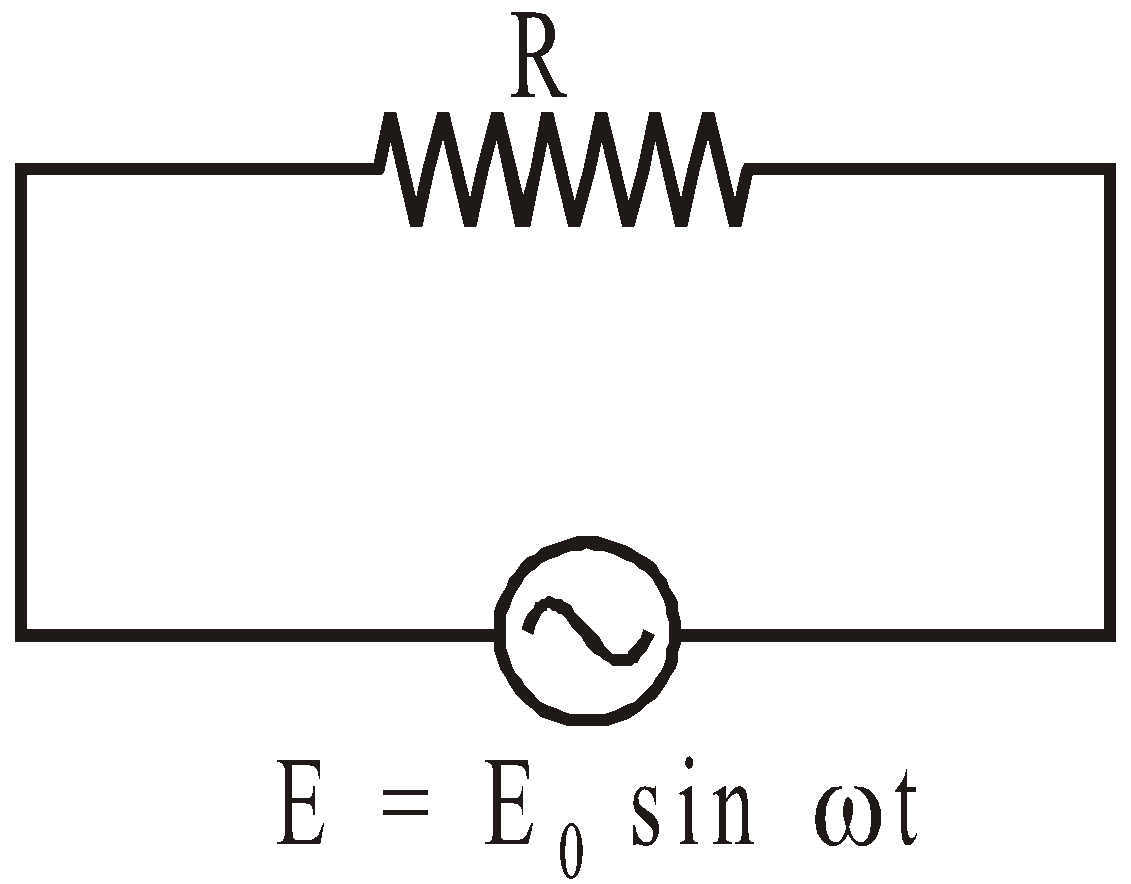
A resistor designed for use in a direct current (dc) circuit is labelled “50 W, 2 Ω”. The resistor is connected in series with an alternating current (ac) power supply of peak potential difference 10 V. What is the average power dissipated by the resistor in the ac circuit?
A 25 W
B 35 W
C 50 W
D100 W
▶️Answer/Explanation
Ans: A
Hence
\(P_{av} =\frac{Eo}{\sqrt{2}} \times \frac{Io}{\sqrt{2}}=\frac{E_0^2}{2R}\)
Since \(I_0=\frac{E_0}{R}\)
\(\therefore\)
\(P_{av} =\frac{E_0^2}{2R} =\frac{10\times 10}{2\times 2} = 25\; W\)
Question
The diagram shows a diode bridge rectification circuit and a load resistor.
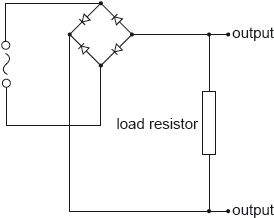
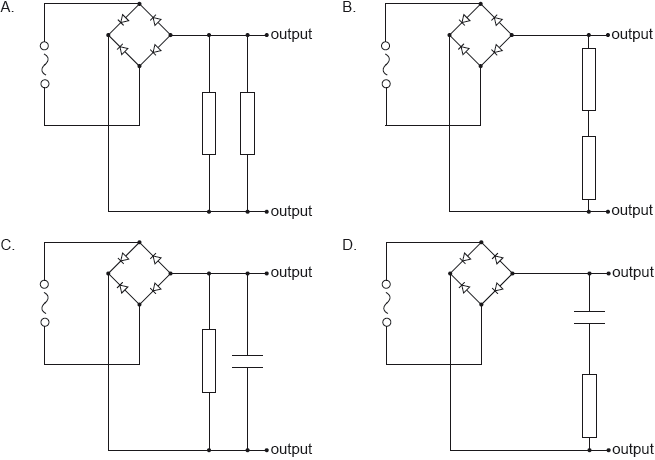
The input is a sinusoidal signal. Which of the following circuits will produce the most smoothed output signal?
▶️Answer/Explanation
Markscheme
C
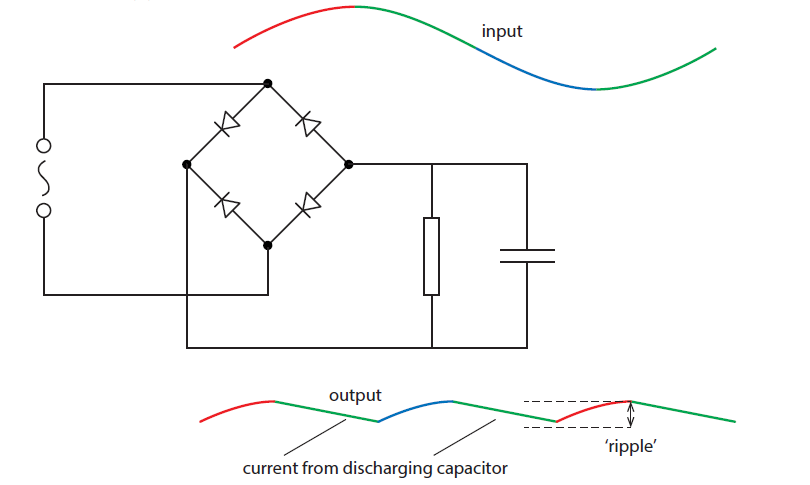
A capacitor in parallel to the load resistor smooths out the output voltage.
For the first half cycle the current is clockwise. The current moves from top to bottom in the load. Now, in the first quarter cycle the capacitor charges. At the end of the first quarter cycle the potential at the top plate of the capacitor is a maximum. In the second quarter cycle (green), the potential at the top plate begins to decrease and so the capacitor discharges, sending current through the load from top to bottom. (The capacitor begins to discharge at the end of the third quarter cycle as well.) The ‘ripple’ is reduced with higher capacitance or load resistance.
Question
The graph shows the variation with time t of the current I in the primary coil of an ideal transformer.
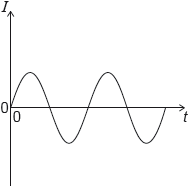
The number of turns in the primary coil is 100 and the number of turns in the secondary coil is 200. Which graph shows the variation with time of the current in the secondary coil?
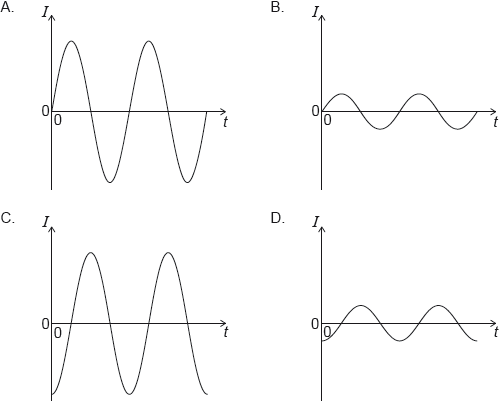
▶️Answer/Explanation
Markscheme
D
We have
\(\frac{\varepsilon _s}{\varepsilon _p}=-\frac{N_s}{N_p} =\frac{I_p}{I_s} =k\)
or
\(\frac{\varepsilon _s}{\varepsilon _p}=-\frac{N_s}{N_p} =\frac{I_p}{I_s} =k\)
\(\frac{I_s}{I_p}=-\frac{N_p}{N_s}=-\frac{100}{200}=\frac{1}{2}\)
Hence
\(I_s= -\frac{I_p}{2}\)
Hence Value is reduced by 2 and a phase of 1800 is induced.
Question
An alternating current (ac) generator produces a peak emf E0 and periodic time T. What are the peak emf and periodic time when the frequency of rotation is doubled?
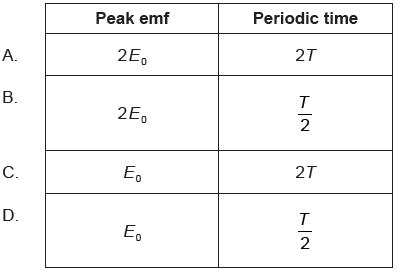
▶️Answer/Explanation
Markscheme
B
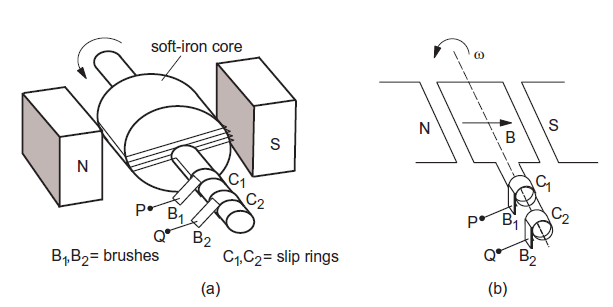
emf Induced as the Coil Rotates
\(\phi=BA\;cos\;\omega t\)
\(-\frac{d\phi}{dt}=BAw\;sin\;\omega t\)
Total emf induced in the coil is
\(\varepsilon = NBA\omega \; sin\;wt = \varepsilon_0\; sin\;\omega t \)
where peak emf \(= NBA\omega\) , angular frequency \(\omega\) and time period \(T =\frac{2\pi}{\omega}\)
Hence if \(\omega\) is doubled \(= NBA\omega\) also doubled . and time period \(T =\frac{2\pi}{\omega}\) is halved.
Question
The ratio \(\frac{{{\text{number of primary turns}}}}{{{\text{number of secondary turns}}}}\) for a transformer is 2.5.
The primary coil of the transformer draws a current of 0.25 A from a 200 V alternating current (ac) supply. The current in the secondary coil is 0.5 A. What is the efficiency of the transformer?
A. 20 %
B. 50 %
C. 80 %
D. 100 %
▶️Answer/Explanation
Markscheme
C
\(\eta =\frac{\varepsilon _sI_s}{\varepsilon _pI_p}\)
Also
\(\frac{\varepsilon _s}{\varepsilon _p} =\frac{N_s}{N_p} =\frac{1}{2.5}\)
Also from given question \(I_s=0.5\) and \(I_p =0.25\)
Hence putting values in equation , we get
\(\eta =\frac{\varepsilon _sI_s}{\varepsilon _pI_p} \times 100\)
\(=\frac{1}{2.5}\times\frac{0.5}{0.25} \times 100 =80 \) %
Question
A direct current (dc) of 5A dissipates a power P in a resistor. Which peak value of the alternating current (ac) will dissipate an average power P in the same resistor?
A. 5A
B. \(\frac{5}{2}{\text{A}}\)
C. \(\frac{5}{{\sqrt 2 }}{\text{A}}\)
D. \({\text{5}}\sqrt 2 \,{\text{A}}\)
▶️Answer/Explanation
Markscheme
D
Now in a/c circuit
\(P =\frac{E_0I_o}{2}=\frac{I_0^2 R}{2}\)
Now power in dc and ac is same , hence
\(\frac{I_0^2 R}{2} =25 R\)
or
\(I_0^2 =50\)
\(I_0 = \sqrt{50} = 5\sqrt{2}\)
