IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.1 – Motion
Topic 2 Weightage : 13 %
All Questions for Topic 2.1 – Distance and displacement , Speed and velocity , Acceleration , Graphs describing motion , Equations of motion for uniform acceleration , Projectile motion , Fluid resistance and terminal speed
Question
The graph shows how the position of an object varies with time in the interval from 0 to 3 s.
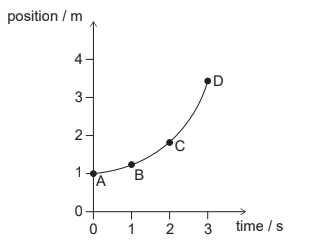
At which point does the instantaneous speed of the object equal its average speed over the interval from 0 to 3 s?
▶️Answer/Explanation
Ans: C
In a graph of position versus time, the instantaneous velocity is the slope of the tangent line at a given point.
The average velocities = \(\bar{v}=\frac{x}{t}=\frac{x_f-x_i}{t_f -t_i}\)
between times . The slope of line connecting end points (average speed) and slope at C are same .
Question
A large stone is dropped from a tall building. What is correct about the speed of the stone after 1 s?
It is decreasing at increasing rate.
It is decreasing at decreasing rate.
It is increasing at increasing rate.
It is increasing at decreasing rate.
▶️Answer/Explanation
Ans: D
As an object falls, it picks up speed. The increase in speed leads to an increase in the amount of air resistance. Eventually, the force of air resistance becomes large enough to balances the force of gravity.
Question
A tennis ball is released from rest and falls vertically through a small distance in air. What is the change in the speed of the ball and the change in the acceleration of the ball as it falls?
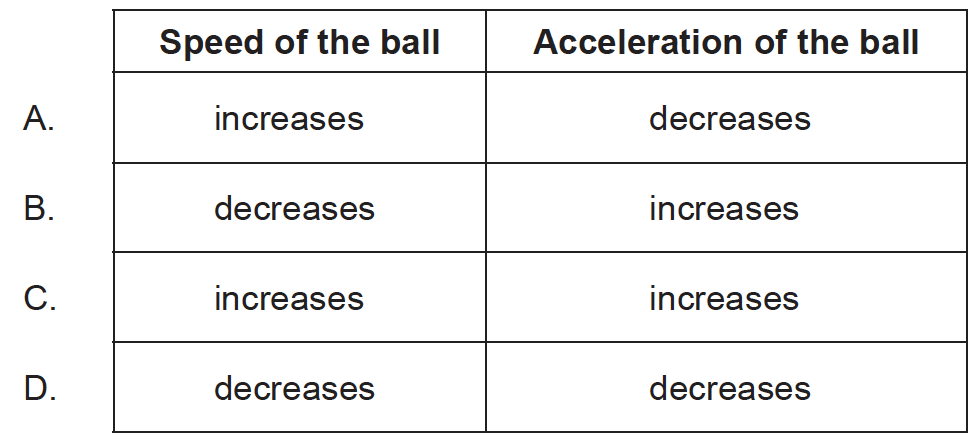
▶️Answer/Explanation
Ans
A
As an object falls, it picks up speed.As an object falls through air, it usually encounters some degree of air resistance. Air resistance is the result of collisions of the object’s leading surface with air molecules.
The increase in speed leads to an increase in the amount of air resistance. Eventually, the force of air resistance becomes large enough to balances the force of gravity.

Question
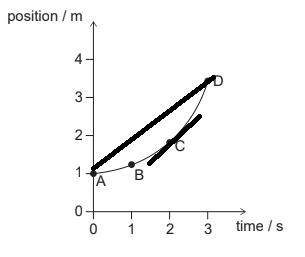
The graph below shows the variation with time t of the velocity v of a car travelling in a straight line.
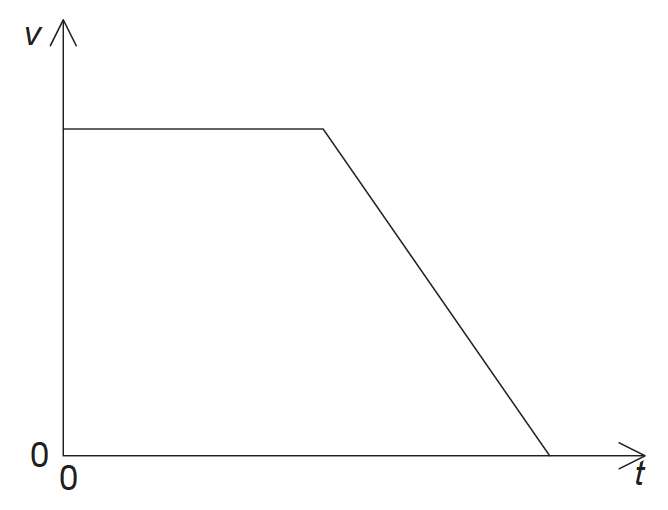
Which graph shows the variation with t of the displacement s of the car?
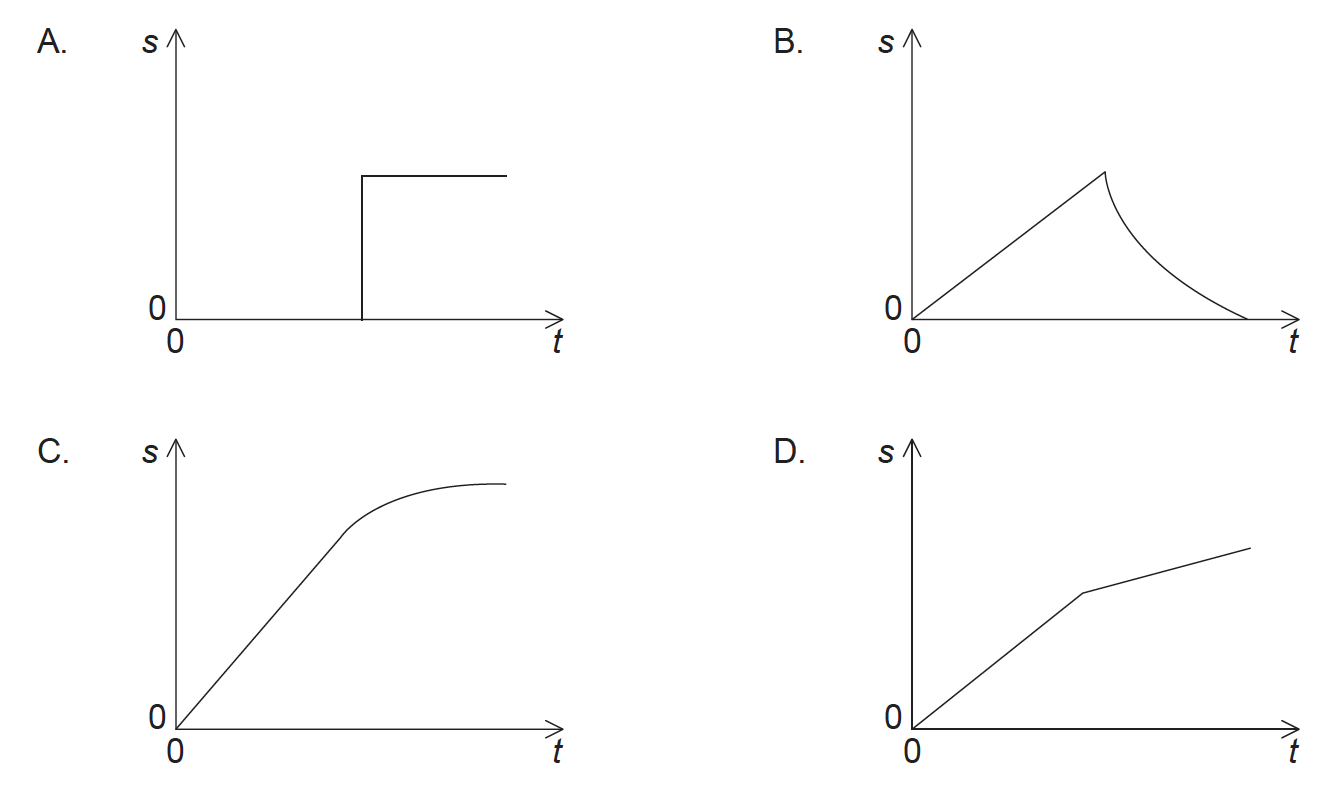
▶️Answer/Explanation
Ans.
C
- Displacement-time graphs show the changing position of an object in motion
- They also show whether an object is moving forwards (positive displacement) or backwards (negative displacement)
Velocity = Gradient of a displacement-time graph
- The greater the slope, the greater the velocity
- A negative gradient = a negative velocity (the object is moving backwards)
Question
A body moves in a straight line. In order for the equations for uniformly accelerated motion to be applied, which condition must be true?
A. A constant net force acts on the body of fixed mass.
B. A constant net force acts on the body.
C. The body falls towards the surface of a planet.
D. The body has an initial velocity of zero.
▶️Answer/Explanation
Ans
A
Uniform Acceleration
Uniform acceleration is the acceleration that does not vary with time. In such cases, Force and the rate of change of velocity remains constant. Since acceleration is a vector quantity, even the direction of motion remains the same in the case of constant acceleration.
Some examples of constant acceleration include
Free-falling object.
A ball rolling down a frictionless slope.
A bicycle whose brakes have been engaged.
Question
The graph shows the variation with time of the velocity of a truck of fixed mass.
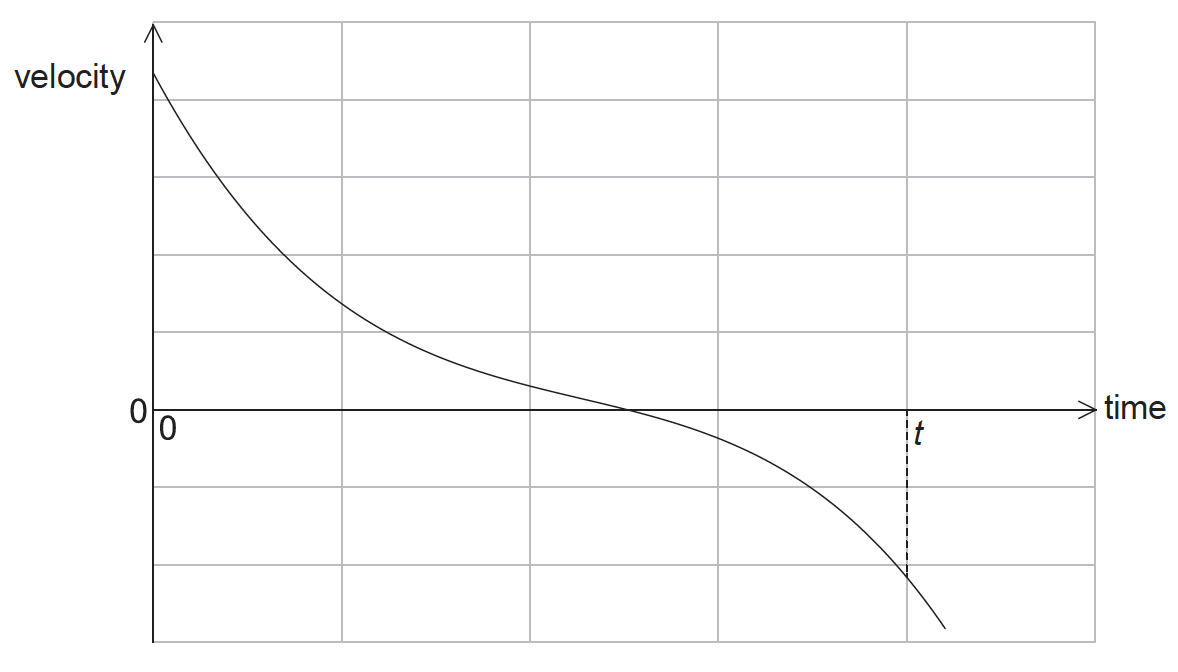
What can be deduced from the graph?
A. The truck is always accelerating.
B. The truck is always moving.
C. The truck is always moving in one direction.
D. The displacement of the truck after time t is zero.
▶️Answer/Explanation
Ans:
A
We know that, slope of the velocity-time graph gives the acceleration of the body. If the velocity-time graph is a curved line, this means its slope changes at every instant which implies that the acceleration of the body changes at every instant. Thus the body is said to be in non-uniform motion.
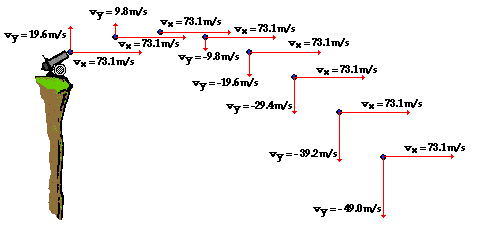
The horizontal component vh and the vertical component vv of velocity of an object are shown on the graphs. Air resistance is negligible.
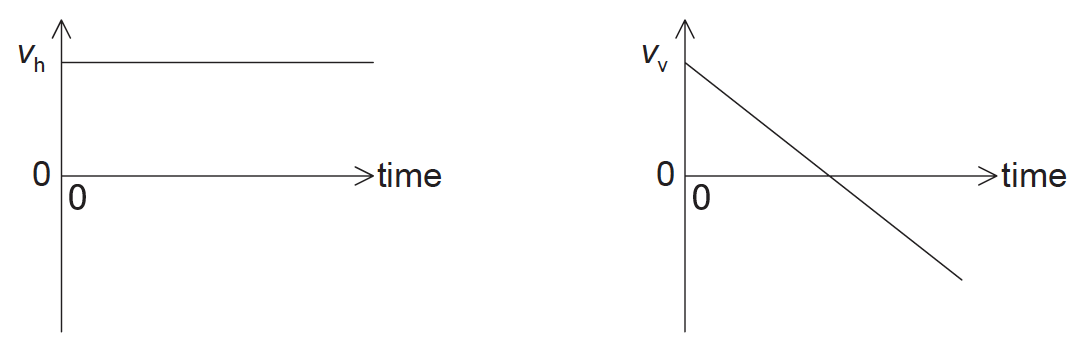
These graphs could represent the motion of an object fired from a cliff
A. vertically upwards.
B. at an angle above the horizontal.
C. horizontally.
D. at an angle below the horizontal.
▶️Answer/Explanation
Ans:
B
projectile is launched upward at an angle to the horizontal. Example is below. Vx is contact but Vy is first decreasing , comes to zero and then increased in opposite direction.