IBDP Physics 2.2 – Forces: IB Style Question Bank – SL Paper 2

IB Physics 2024
IB Biology 2024
IB Chemistry 2024
IB Math MAI & MAA

IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics

Topic 2.2 – Forces

Topic 2 Weightage : 13 % 

All Questions for Topic 2.2 – Objects as point particles , Free-body diagrams , Translational equilibrium , Newton’s laws of motion ,Solid friction

Question

A company delivers packages to customers using a small unmanned aircraft. Rotating horizontal blades exert a force on the surrounding air. The air above the aircraft is initially stationary.

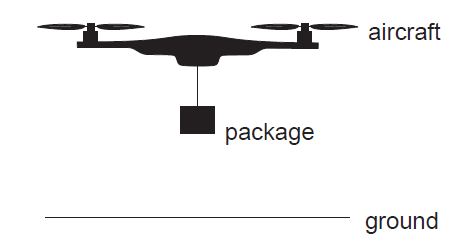
The air is propelled vertically downwards with speed v. The aircraft hovers motionless above the ground. A package is suspended from the aircraft on a string. The mass of the aircraft is

0.95 kg and the combined mass of the package and string is 0.45 kg. The mass of air pushed downwards by the blades in one second is 1.7 kg.

a. State the value of the resultant force on the aircraft when hovering. [1]

b. Outline, by reference to Newton’s third law, how the upward lift force on the aircraft is achieved. [2]

c. Determine ν. State your answer to an appropriate number of significant figures. [3]

d. The package and string are now released and fall to the ground. The lift force on the aircraft remains unchanged. Calculate the initial acceleration of the aircraft. [2]

▶️Answer/Explanation

Ans:

a. Ans : zero ✓

b. Blades exert a downward force on the air ✓
air exerts an equal and opposite force on the blades «by Newton’s third law» OR
air exerts a reaction force on the blades «by Newton’s third law» ✓

c.

«lift force/change of momentum in one second» = 1.7 v 

1.7 v  =  (0.95 + 0.45) X 9.81

v = 8.1 “ ms-1 ” AND answer expressed to 2 sf only

Allow 8.2 from g = 10 ms –2

d.

vertical force = lift force – weight OR = 0.45 x 9.81 OR = 4.4 ” N ” 

acceleration = (0.45 * 9.81)/0.95 =4.6 m s-2 

Question

The Rotor is an amusement park ride that can be modelled as a vertical cylinder of inner radius R rotating about its axis. When the cylinder rotates sufficiently fast, the floor drops out and the passengers stay motionless against the inner surface of the cylinder. The diagram shows a person taking the Rotor ride. The floor of the Rotor has been lowered away from the person.

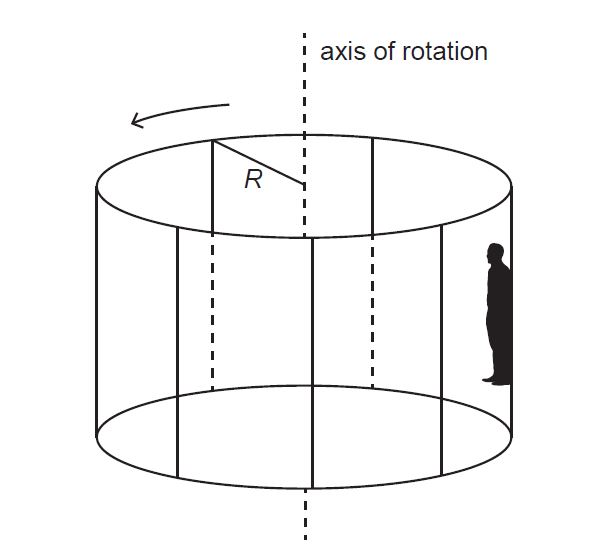
a. Draw and label the free-body diagram for the person.

b. The person must not slide down the wall. Show that the minimum angular velocity ω of the cylinder for this situation is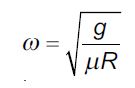

where μ is the coefficient of static friction between the person and the cylinder.

c. The coefficient of static friction between the person and the cylinder is 0.40. The radius of the cylinder is 3.5 m. The cylinder makes 28 revolutions per minute. Deduce whether the person will slide down the inner surface of the cylinder. 

▶️Answer/Explanation

Ans:

a.

arrow downwards labeled weight / W / mg and arrow upwards labeled friction / F  arrow horizontally to the left labeled “ normal “ reaction / N

Ignore point of application of the forces but do not allow arrows that do not touch the object. Do not allow horizontal force to be labeled ‘centripetal’ or R.

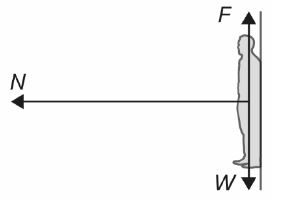
b. See F = μN AND N = mR w 2 ” Substituting for N ” μmR w 2 = mg 

c. 

Question

This question is about the motion of a bicycle.

A cyclist is moving up a slope that is at an angle of 19° to the horizontal. The mass of the cyclist and the bicycle is 85 kg.

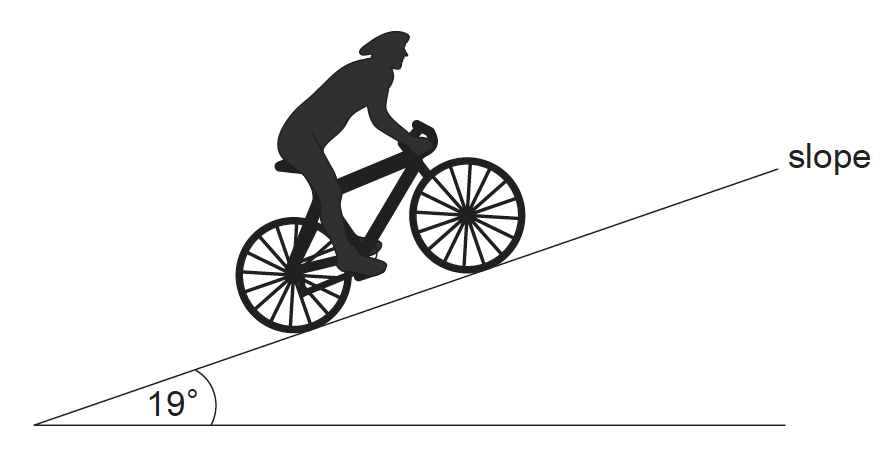
a. Calculate the

(i) component of the weight of the cyclist and bicycle parallel to the slope.

(ii) normal reaction force on the bicycle from the slope. [3]

b. At the bottom of the slope the cyclist has a speed of 5.5ms–1. The cyclist stops pedalling and applies the brakes which provide an additional decelerating force of 250 N. Determine the distance taken for the cyclist to stop. Assume air resistance is negligible and that there are no other frictional forces. [4] 
▶️Answer/Explanation

Markscheme

a. (i) (weight) = 85 × 9.81(=834N); (if 850 (N) seen, award this mark)
component =(834×sin19=)271 (N);
Allow use of g=10ms–2. Answer is 277 (N).

(ii) component=(834×cos19=) 788 (N);
Allow use of g=10ms –2. Answer is 804 (N).
Allow a bald correct answer.
Do not award ECF if cos used in (a)(i) and sin used in (a)(ii).

b. total decelerating force =271+250(=521N);

acceleration \( = \left(  –  \right)\frac{{521}}{{85}}\left( { =  – 6.13{\rm{m}}{{\rm{s}}^{ – 2}}} \right)\);
\(s = \frac{{{v^2} – {u^2}}}{{2a}}\);
2.47 (m);} (signs must be consistent for this mark, ie: if acceleration assumed positive, look for negative distance)
Allow use of g=10. Answers are 527 N, 6.2ms–2, 2.44 m.

or

total decelerating force =271+250(=521N) ;
initial kinetic energy \( = \frac{1}{2}m{v^2} = 1290{\rm{ J}}\)
\({\rm{distance = }}\frac{{{\rm{energy lost}}}}{{{\rm{force}}}} = \frac{{1290}}{{521}}\)
2.47 (m); 

Question

This question is about forces.

A stone block is pulled at constant speed up an incline by a cable attached to an electric motor.

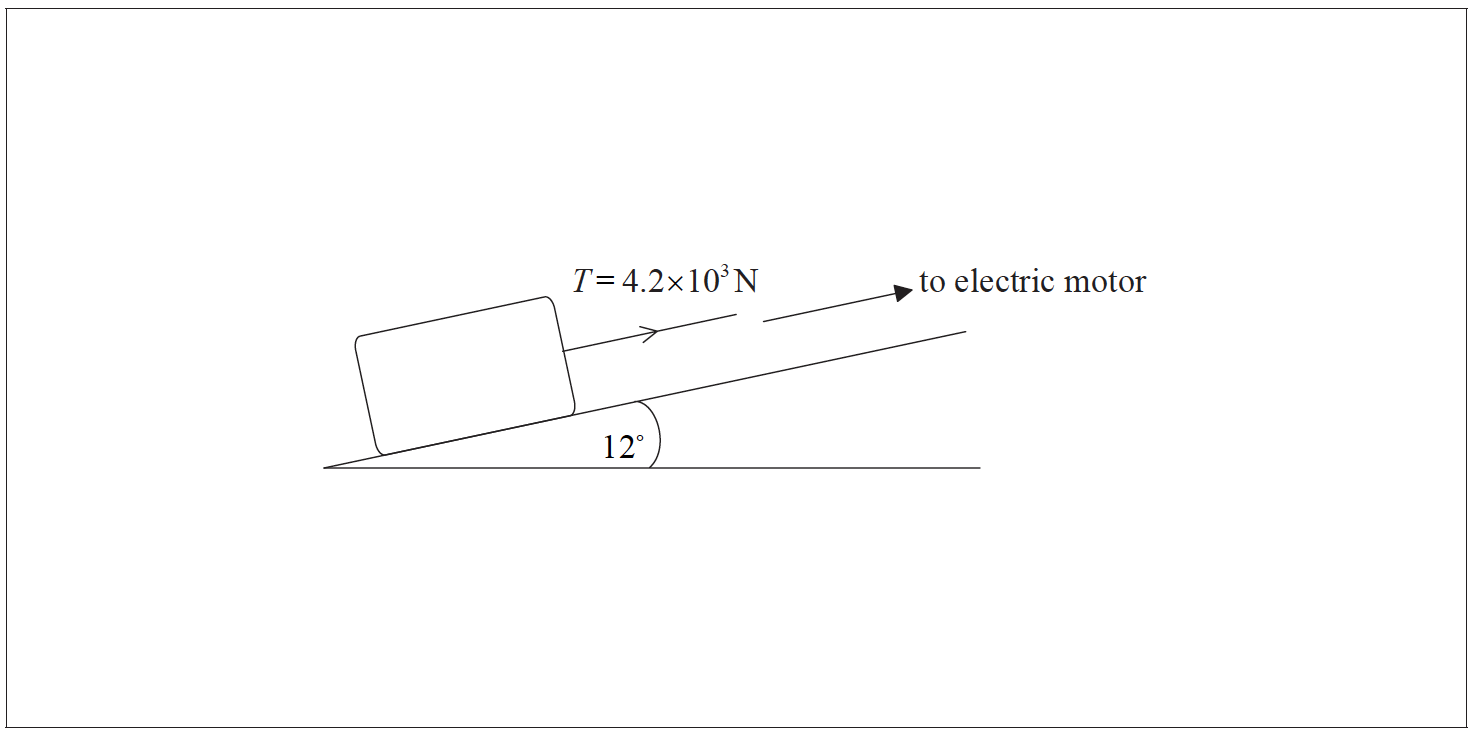
The incline makes an angle of 12° with the horizontal. The weight of the block is 1.5×104N and the tension T in the cable is 4.2×103N.

a. On the diagram draw and label arrows that represent the forces acting on the block. [2]

b. Calculate the magnitude of the friction force acting on the block. [3] 
▶️Answer/Explanation

Markscheme

a. 

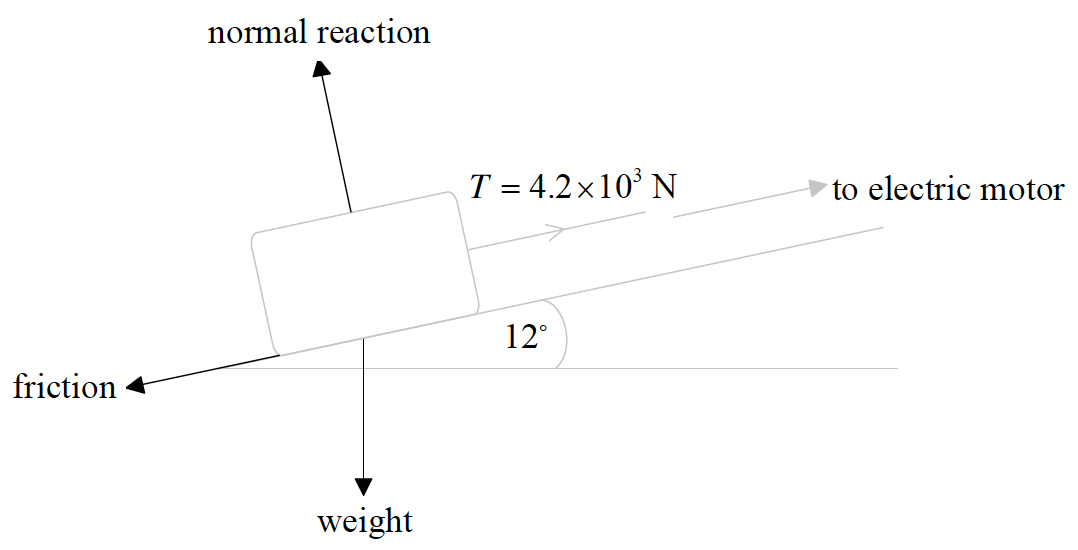
(normal) reaction/N/R and weight/force of gravity/gravity force/gravitational force/mg/w/W with correct directions;
friction/frictional force/F/Ff with arrow pointing down ramp along surface of ramp;
Do not allow “gravity” as label. Do not allow “drag” as label for friction.

b. recognize that friction=T-W sin θ;

W sin θ=3.1×103N;
friction=1.1×103N; 

Question

This question is in two parts. Part 1 is about Newton’s laws and momentum. Part 2 is about the greenhouse effect.

Part 1 Newton’s laws and momentum

Part 2 The greenhouse effect

a. State the condition for the momentum of a system to be conserved. [1]

b. A person standing on a frozen pond throws a ball. Air resistance and friction can be considered to be negligible.

(i) Outline how Newton’s third law and the conservation of momentum apply as the ball is thrown.

(ii) Explain, with reference to Newton’s second law, why the horizontal momentum of the ball remains constant whilst the ball is in flight. [5]

c. The maximum useful power output of a locomotive engine is 0.75 M W. The maximum speed of the locomotive as it travels along a straight horizontal track is 44 m s–1. Calculate the frictional force acting on the locomotive at this speed. [2]
d. The locomotive engine in (c) gives a truck X a sharp push such that X moves along a horizontal track and collides with a stationary truck Y. As a result of the collision the two trucks stick together and move off with speed v. The following data are available.

Mass of truck X=3.7×103 kg
Mass of truck Y=6.3×103 kg
Speed of X just before collision=4.0 m s–1

(i) Calculate v.

(ii) Determine the kinetic energy lost as a result of the collision. [4]

e. The trucks X and Y come to rest after travelling a distance of 40 m along the horizontal track. Determine the average frictional force acting on X and Y. [3]
f. Nuclear fuels, unlike fossil fuels, produce no greenhouse gases.

(i) Identify two greenhouse gases.

(ii) Discuss, with reference to the mechanism of infrared absorption, why the temperature of the Earth’s surface would be lower if there were no greenhouse gases present in the atmosphere. [5]

g. Outline how an increase in the amount of greenhouse gases in the atmosphere of Earth could lead to an increase in the rate at which glaciers melt and thereby a reduction of the albedo of the Earth’s surface. [3] 
▶️Answer/Explanation

Markscheme

a. the net (external) force acting on the system is zero / no force acting on system / system is isolated;

b. (i) no external force/system is isolated so change in momentum is zero; { (do not accept momentum is conserved/constant)

force on ball must be equal and opposite to force on the person;
so ball and person/Earth/pond move in opposite directions;

(ii) Newton’s second law states that the rate of change of momentum is equal/proportional/directly proportional to the force acting;
the horizontal force acting on the ball is zero therefore the momentum must be constant/the rate of change of momentum is zero;

or

Newton’s second law can be expressed as the force acting is equal to the product of mass and acceleration;
the horizontal force acting on the ball is zero therefore the acceleration is zero so velocity is constant (and therefore momentum is constant);

c.

\(F = \frac{P}{v}\) or \(\frac{{0.75 \times {{10}^6}}}{{44}}\);
17kN;

d. (i) 3.7×4.0=10×v;

v=1.5ms−1;

(ii) KE lost\( = \frac{1}{2}\left[ {3.7 \times {{10}^3} \times {{4.0}^2}} \right] – \frac{1}{2}\left[ {10 \times {{10}^3} \times {{1.5}^2}} \right]\);
=18kJ;

e. initial KE\( = \left( {\frac{1}{2}\left[ {10 \times {{10}^3} \times {{1.5}^2}} \right] = } \right)11250{\rm{J}}\);

friction\( = \frac{{11250}}{{40}}\);
=280 N;

or

use of kinematic equation to give a=0.274ms–1;
use of F(=ma)=10×103a;
270/280 N;

f.

(i) methane/CH4, water vapour/H2O, carbon dioxide/CO2, nitrous oxide/N2O;
Award [1] for any two of the above.

(ii) mechanism:
mention of resonance;
natural frequency of (resonating) greenhouse gas molecules is same as that of infrared radiation from Earth;

or

mention of energy level differences;
differences between energy levels of greenhouse gas molecules matches energy of infrared radiation from Earth;

explanation:
less infrared trapped if absorption is reduced;
so more infrared is transmitted through atmosphere;

or

more infrared is trapped if absorption is increased;
so more infrared is re-radiated back to Earth;
Allow only one variant for each alternative.

g. more greenhouse gas therefore more infrared radiated back to Earth;

leading to an increase in temperature of glaciers/surface;
less glacier area so less reflection from glacier surface / OWTTE;
albedo defined as \(\frac{{{\rm{amount of radiation reflected}}}}{{{\rm{amount of radiation absorbed}}}}\) therefore albedo reduced; 

Question

This question is about circular motion.

A ball of mass 0.25 kg is attached to a string and is made to rotate with constant speed v along a horizontal circle of radius r = 0.33m. The string is attached to the ceiling and makes an angle of 30° with the vertical.

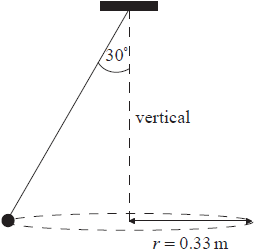
a (i) On the diagram above, draw and label arrows to represent the forces on the ball in the position shown.

(ii) State and explain whether the ball is in equilibrium. [4]

b .

Determine the speed of rotation of the ball. [3] 

▶️Answer/Explanation

Markscheme

a. (i) [1] each for correct arrow and (any reasonable) labelling;

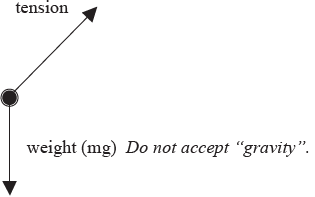
Award [1 max] for arrows in correct direction but not starting at the ball.

(ii) no;
because the two forces on the ball can never cancel out / there is a net force on
the ball / the ball moves in a circle / the ball has acceleration/it is changing
direction; 
Award [0] for correct answer with no or wrong argument.

b.

\(T\left( { = \frac{{mg}}{{\cos {{30}^ \circ }}}} \right) = 2.832{\rm{N}}\);
\(\frac{{m{v^2}}}{r} = T\sin {30^ \circ }\);
\(v = \left( {\sqrt {\frac{{Tr\sin {{30}^ \circ }}}{m}}  = \sqrt {\frac{{2.832 \times 0.33 \times \sin {{30}^ \circ }}}{{0.25}}} } \right) = 1.4{\rm{m}}{{\rm{s}}^{ – 1}}\);

or

\(T\cos {30^ \circ } = mg\);
\(T\sin {30^ \circ } = \frac{{m{v^2}}}{r}\);
\(v = \left( {\sqrt {gr\tan {{30}^ \circ }}  = \sqrt {9.81 \times 0.33 \times \tan {{30}^ \circ }} } \right) = 1.4{\rm{m}}{{\rm{s}}^{ – 1}}\); 

More DP Physics SL Paper 2 Questions..

Related Links

Scroll to Top