IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.4 – Momentum and impluse
Topic 2 Weightage : 13 %
All Questions for Topic 2.4 – Newton’s second law expressed in terms of rate of change of momentum ,Impulse and force–time graphs , Conservation of linear momentum , Elastic collisions, inelastic collisions and explosions
Question
A ball undergoes an elastic collision with a vertical wall. Which of the following is equal to zero?
A The change of the magnitude of linear momentum of the ball
B The magnitude of the change of linear momentum of the ball
C The rate of change of linear momentum of the ball
D The impulse of the force on the ball
▶️Answer/Explanation
Ans: A
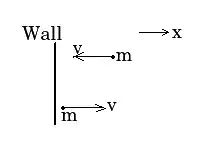
The ball bounces back with the same speed i.e v
\(\therefore \vec{v}=-\vec{u}\)
Magnitude of momentum before collision =\(\left | mu \right |\)
Magnitude of momentum after collision =\(\left | mv \right |=\left | mu \right |\)
Hence change in Magnitude of momentum = 0
but Magnitude of change in momentum = \(\left | \vec{P_2} -\vec{P_1} \right |= \left | m\vec{v}-m\vec{u}\right |= mv-(-mv)=2mv\)
Question
Two identical spheres, each of mass m and speed v, travel towards each other on a frictionless surface in a vacuum.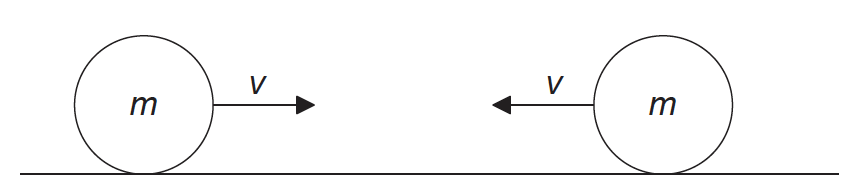
The spheres undergo a head-on elastic collision.
Which statement correctly describes the spheres after the collision?
A. The total momentum of the spheres is 2mv.
B. Each sphere has zero momentum.
C. The total kinetic energy of the spheres is mv2.
D. Each sphere has zero kinetic energy.
▶️Answer/Explanation
Markscheme
C
Ref: https://www.iitianacademy.com/ib-physics-topic-2-mechanics-2-4-momentum-and-impulse-study-notes/
Before Collision
Total Momentum \( = m_1u_1+m_2u_2 = mu+m(-u) =0\)
Total Energy:
\(\frac{1}{2}m_1(v_1)^2 +\frac{1}{2}m_2(v_2)^2 =\frac{1}{2}mv^2+\frac{1}{2}mv^2 =mv^2\)
Question
In the collision between two bodies, Newton’s third law
A. only applies if momentum is conserved in the collision.
B. only applies if energy is conserved in the collision.
C. only applies if both momentum and energy are conserved in the collision.
D. always applies.
▶️Answer/Explanation
Markscheme
D
Newton’s third law of motion is naturally applied to collisions between two objects. In a collision between two objects, both objects experience forces that are equal in magnitude and opposite in direction. Such forces often cause one object to speed up (gain momentum) and the other object to slow down (lose momentum).
Examiners report
Candidates are often under the misapprehension that there are conditions upon Newton’s third law. It should be stressed that it is always true irrespective of energy or momentum considerations; and it does not depend upon the state of motion of the bodies in contact.
Question
A ball X moving horizontally collides with an identical ball Y that is at rest.
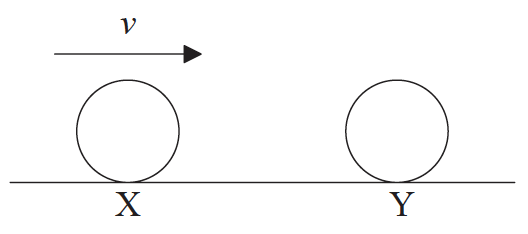
X strikes Y with speed v.
What is a possible outcome of the collision?
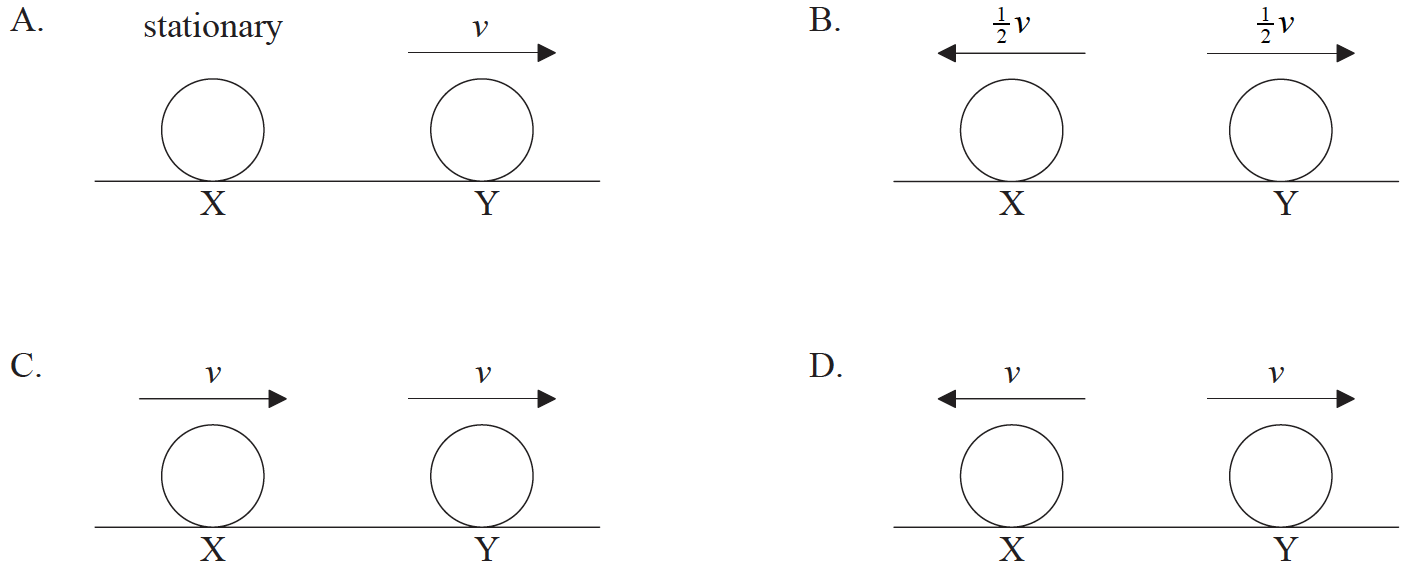
▶️Answer/Explanation
Markscheme
A
Ref: https://www.iitianacademy.com/ib-physics-topic-2-mechanics-2-4-momentum-and-impulse-study-notes/

- If M1 = M2 and u2 = 0 then v1 = 0 and v2 = u1. Under this condition the first particle comes to rest and the second particle moves with the velocity of first particle after collision. In this state there occurs maximum transfer of energy.
Question
A ball is moving horizontally and strikes a vertical wall from which it rebounds horizontally. The sketch graph shows how the contact force F between ball and wall varies with time of contact t.
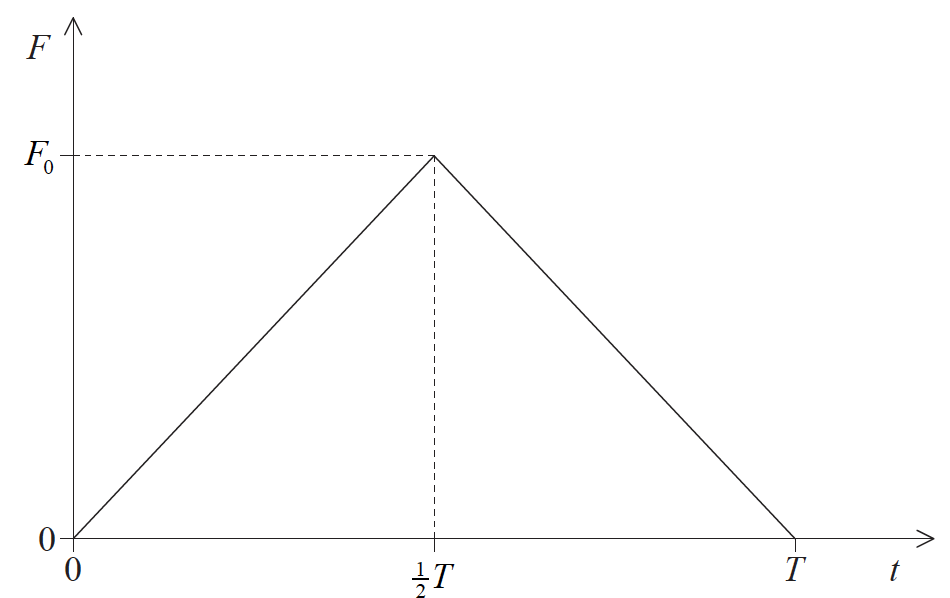
The maximum value of F is F0 and the total time of contact between ball and wall is T.
What is the change in momentum of the ball?
A. \(\frac{{{F_0}T}}{2}\)
B. \({F_0}T\)
C. \(\frac{{{F_0}}}{{2T}}\)
D. \(\frac{{{F_0}}}{T}\)
▶️Answer/Explanation
Markscheme
A
Ref: https://www.iitianacademy.com/ib-physics-topic-2-mechanics-2-4-momentum-and-impulse-study-notes/
Impulse
When two bodies collide, they exert forces on each other while in contact. The momentum of each body is changed due to the force on it exerted by the other. On an ordinary scale, the time duration of this contact is very small and yet the change in momentum is sizeable. This means that the magnitude of the force must be large on an ordinary scale. Such large forces acting for a very short duration are called impulsive forces. The force may not be uniform while the contact lasts.
The change in momentum produced by such an implusive force is
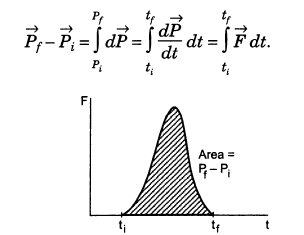
Now area under the F-t curve is
\(\frac{1}{2} \times T \times F_0\) = Change in Momentum
Question
An insect of mass m jumps vertically from rest to a height h. The insect releases the energy needed for the jump in time Δt. What is the estimate for the power developed by the insect?
A. mgh Δt
B. mh Δt
C. \(\frac{{mgh}}{{\Delta t}}\)
D. \(\frac{{mh}}{{\Delta t}}\)
▶️Answer/Explanation
Markscheme
C
