IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 4.5 Standing waves
Topic 4 Weightage : 5 %
All Questions for Topic 4.5 – The nature of standing waves , Boundary conditions , Nodes and antinodes
Question
A metal rod of length 45 cm is clamped at its mid point. The speed of sound in the metal rod is \(1500\; ms^{-1}\) and the speed of sound in air is \(300\; ms^{-1}\). The metal rod vibrates at its first harmonic. What is the wavelength in air of the sound wave produced by the metal rod?
A 4.5 cm
B 9.0 cm
C 18 cm
D 90 cm
▶️Answer/Explanation
Ans: C
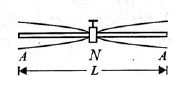
As rod is clamped at middle, its a node and both ends are antinodes
\(\therefore \frac{\lambda}{4}+\frac{\lambda}{4}=\frac{\lambda}{2}=L=0.45 \;m\)
or
\(\lambda =0.45 \times 2 =0.90\)
\(v=f \lambda\)
\(f= \frac{v}{\lambda} =\frac{1500}{0.90}\)
With same frequency air will also vibrate
\(\lambda_{air} =\frac{v_{air}}{f}=\frac{300}{\frac{1500}{0.90}}=\frac{0.96}{5}=0.18 \;m = 18\;cm\)
Question
A string stretched between two fixed points sounds its second harmonic at frequency f.

Which expression, where n is an integer, gives the frequencies of harmonics that have a node at the centre of the string?
A. \(\frac{{n + 1}}{2}f\)
B. nf
C. 2nf
D. (2n + 1)f
▶️Answer/Explanation
Markscheme
B
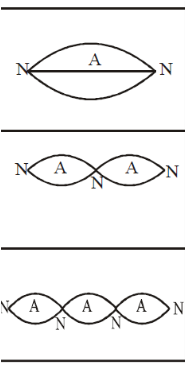
\(n\frac{\lambda}{2}=L\)
\(\therefore f_n =\frac{v}{\lambda} =\frac{nv}{2L}\) —(1)
now for first Harmonic \(n=1\)
or
\(\lambda = 2L\)
\(\therefore f=\frac{v}{\lambda}=\frac{v}{2L}\)
putting this value in equation (1)
\(f_n =\frac{nv}{2L} =nf\)
Question
The diagram shows a second harmonic standing wave on a string fixed at both ends.
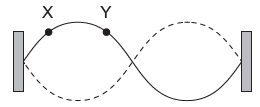
What is the phase difference, in rad, between the particle at X and the particle at Y?
A. 0
B. \(\frac{\pi }{4}\)
C. \(\frac{\pi }{2}\)
D. \(\frac{{3\pi }}{4}\)
▶️Answer/Explanation
Markscheme
A
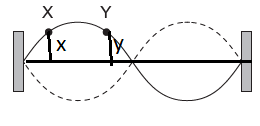
We have phase difference \(\phi \) as
\(\phi = \frac{2\pi}{\lambda}\times \Delta x\)
here
\(\Delta x =x-y=0\)
hence
\(\phi =0\)
