IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 5.2 – Heating effect of electric currents
Topic 5 Weightage : 8 %
All Questions for Topic 5.2 – Circuit diagrams , Kirchhoff’s circuit laws , Heating effect of current and its consequences , Resistance expressed as R = V/I , Ohm’s law , Resistivity , Power dissipation
Question
Two conductors S and T have the V/I characteristic graphs shown below.
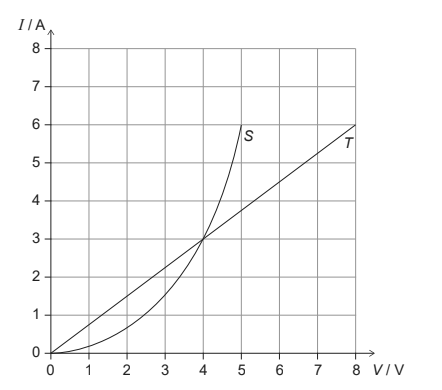
When the conductors are placed in the circuit below, the reading of the ammeter is 6.0 A.
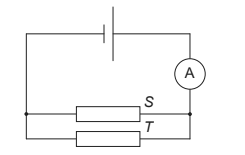
What is the emf of the cell?
A 4.0 V
B 5.0 V
C 8.0 V
D 13 V
▶️Answer/Explanation
Ans: A
The equation \(V=iR\) is the defining equation for resistance, and it applies to all conducting devices, whether they obey Ohm’s law or not. If we measure the potential difference \(V \) across, and the current \(i\) through, any device, even a pn junction diode, we can find its resistance at that value of \(V\) as \(R=\frac{V}{i}\)
\(\frac{1}{R_T}=\frac{6-0}{8-0}=\frac{3}{4}\)
From the graph , V and I is not defined for V equal 8 0r 13 hence these can not be correct options.
If emf = 5 V
Then from graph we have
\(\frac{1}{R_S} =\frac{6}{5}\)
hence
\(\frac{1}{R} =\frac{1}{R_S} +\frac{1}{R_T} =\frac{6}{5}+\frac{6}{8} =1.95\)
\(i=v \times \frac{1}{R} =5\times 1.95 =9.75 \neq 6\)
but current is 6 A hence this can not be correct option
Now verify for emf = \(4v\)
\(\frac{1}{R_S} =\frac{3}{4}\)
\(\frac{1}{R_T} =\frac{6}{8}\)
\(\frac{1}{R} =\frac{1}{R_S} +\frac{1}{R_T} =\frac{3}{4}+\frac{6}{8} =\frac{3}{2}\)
\(i=v \times \frac{1}{R} =4\times \frac{3}{2} =6 \)
which is true as given current is 6 A. Hence correct option is A
Question
An electric motor raises an object of weight 500 N through a vertical distance of 3.0 m in 1.5 s. The current in the electric motor is 10 A at a potential difference of 200 V. What is the efficiency of the electric motor?
A. 17 %
B. 38 %
C. 50 %
D. 75 %
▶️Answer/Explanation
Ans: C
Electric energy supplied by Motor = \(Pt=VIt\)
Given V= 200v , I = 10 A and t = 1.5 s, weight = 500 N ,vertical distance =3m
Electric energy \(E = VIt = 200 \times 10\times 1.5 =3000 \; J \)
Now Work Output = \(mgh = 500 \times 3 = 1500 \); J)
\(efficiency = \frac{Output }{Input}\times 100= \frac{1500}{3000}\times 100 = 50 \;%\)
Question
Three resistors are connected as shown. What is the value of the total resistance between X and Y?
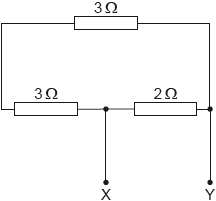
A. 1.5 Ω
B. 1.9 Ω
C. 6.0 Ω
D. 8.0 Ω
▶️Answer/Explanation
Markscheme
A
\(3\Omega\) resistance are in series , equivalent of which, is in parallel to \(2\Omega\)
\(R_1= 3+3 = 6 \Omega\)
\(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{2}=\frac{1}{6}+\frac{1}{2} =\frac{4}{6}\)
\(\therefore R= \frac{6}{4}=1.5 \Omega\)
Question
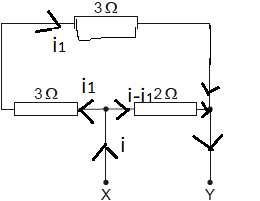
Kirchhoff’s laws are applied to the circuit shown.
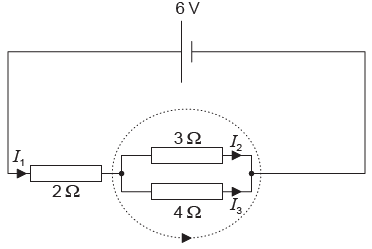
What is the equation for the dotted loop?
A. 0 = 3I2 + 4I3
B. 0 = 4I3 − 3I2
C. 6 = 2I1 + 3I2 + 4I3
D. 6 = 3I2 + 4I3
▶️Answer/Explanation
Markscheme
B
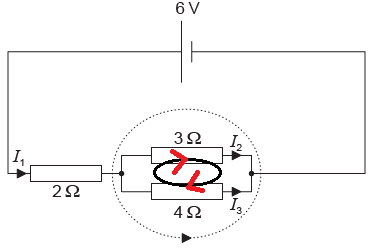
Along the loop \(IR\) is taken positive and opposite to it negative. Also emf in this loop is zero as there is no external cell
Hence
\(3\times I_2 -4\times I_3 = 0\)
\(or\)
\(4\times I_3 -3\times I_2 =0\)
