IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 7.2 – Nuclear reactions
Topic 7 Weightage : 7%
All Questions for Topic 7.2 – The unified atomic mass unit , Mass defect and nuclear binding energy , Nuclear fission and nuclear fusion
Question
a. One possible fission reaction of uranium-235 (U-235) is
\[{}_{92}^{235}{\rm{U}} + {}_0^1{\rm{n}} \to {}_{56}^{144}{\rm{Ba}} + {}_{36}^{89}{\rm{Kr}} + 3{}_0^1{\rm{n}}\]
The following data are available.
Mass of one atom of U-235 = 235 u
Binding energy per nucleon for U-235 = 7.59 MeV
Binding energy per nucleon for Xe-140 = 8.29 MeV
Binding energy per nucleon for Sr-94 = 8.59 MeV
i. State what is meant by binding energy of a nucleus.[1]
ii. Outline why quantities such as atomic mass and nuclear binding energy are often expressed in non-SI units. [1]
iii. Show that the energy released in the reaction is about 180 MeV. [1]
b. A nuclear power station uses U-235 as fuel. Assume that every fission reaction of U-235 gives rise to 180 MeV of energy.
- Estimate, in J kg–1, the specific energy of U-235. [2]
ii. The power station has a useful power output of 1.2 GW and an efficiency of 36 %. Determine the mass of U-235 that undergoes fission in one day. [2]
c. A sample of waste produced by the reactor contains 1.0 kg of strontium-94 (Sr-94). Sr-94 is radioactive and undergoes beta-minus (β–) decay into a daughter nuclide X. The reaction for this decay is
\(_{{\mkern 1mu} {\mkern 1mu} 38}^{94}{\text{Sr}} \to _{X} + _{ – 1}^{\,\,\,0}{\text{e}} + {\overline {\text{V}} _{\text{e}}}\)
i. Write down the proton number of nuclide X.[1]
ii. The graph shows the variation with time of the mass of Sr-94 remaining in the sample.
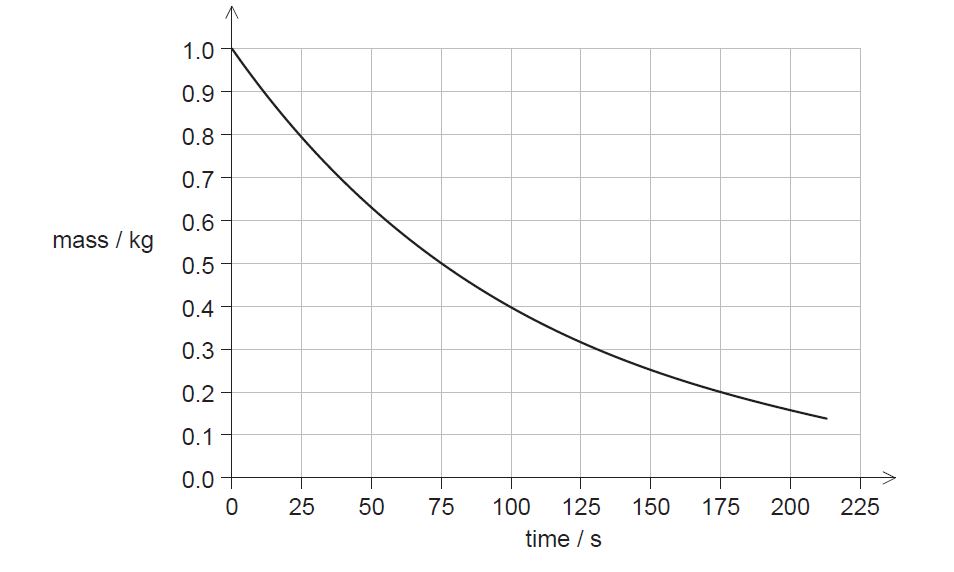
State the half-life of Sr-94.[1]
iii. Calculate the mass of Sr-94 remaining in the sample after 10 minutes.[2]
▶️Answer/Explanation
Ans:
a.i. energy required to «completely» separate the nucleons
OR
energy released when a nucleus is formed from its constituent nucleons
aii. The values «in SI units» would be very small
aiii. 140×8.29 + 94x 8.59 − 235x 7.59OR 184 «MeV
b.i. see − «energy »180 x106x 1.60x 10-19 AND «mass =» 235x 1.66x 10-27
= 7.4x 1013 «J kg-1
b.ii. energy produced in one day =1.2×109x24x3600/0.36 = 2.9×1014 j
mass = 2.9×1014/7.4×1013=3.9 kg
c.i. 39
c.ii. 75 s
c.iii.
ALTERNATIVE 1
10 min = 8 t1/2
mass remaining =1.0x(1/2)8=3.9×10-3 kg
ALTERNATIVE 2
decay constant =ln2/75 =9.24×10-3 s-1
mass remaining =1.0xe-9.24×10-3×600=3.9×10-3 kg
Rhodium-106 (\(_{\,\,\,45}^{106}{\text{Rh}}\)) decays into palladium-106 (\(_{\,\,\,46}^{106}{\text{Pd}}\)) by beta minus (β–) decay.
The binding energy per nucleon of rhodium is 8.521 MeV and that of palladium is 8.550 MeV.
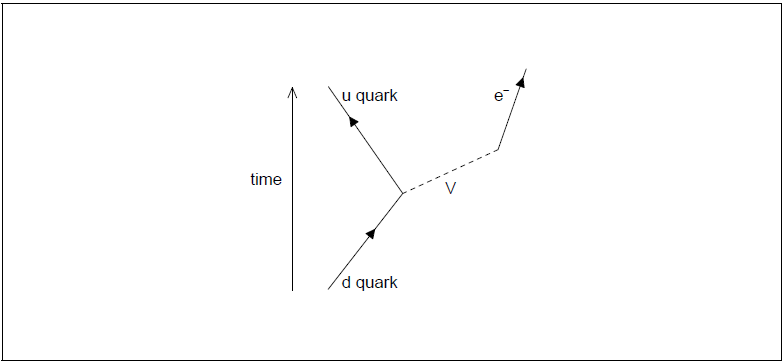
β– decay is described by the following incomplete Feynman diagram.
a.
Rutherford constructed a model of the atom based on the results of the alpha particle scattering experiment. Describe this model.[2]
State what is meant by the binding energy of a nucleus.[1]
Show that the energy released in the β– decay of rhodium is about 3 MeV.[1]
Draw a labelled arrow to complete the Feynman diagram.[1]
Identify particle V.[1]
▶️Answer/Explanation
Markscheme
a.
«most of» the mass of the atom is confined within a very small volume/nucleus
«all» the positive charge is confined within a very small volume/nucleus
electrons orbit the nucleus «in circular orbits»[2 marks]
the energy needed to separate the nucleons of a nucleus
OR
energy released when a nucleus is formed from its nucleons
Allow neutrons AND protons for nucleons
Don’t allow constituent parts[1 mark]
Q = 106 × 8.550 − 106 × 8.521 = 3.07 «MeV»
«Q ≈ 3 Me V»[1 mark]
line with arrow as shown labelled anti-neutrino/\(\bar v\)
Correct direction of the “arrow” is essential
The line drawn must be “upwards” from the vertex in the time direction i.e. above the horizontal
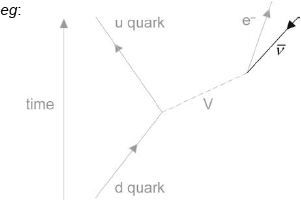[1 mark]
V = W– [1 mark]
a.A particular K meson has a quark structure \({\rm{\bar u}}\)s. State the charge on this meson.[1]
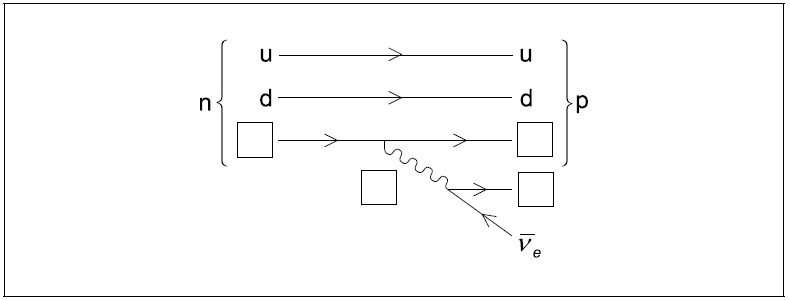
Label the diagram by inserting the four missing particle symbols.[2]
Carbon-14 (C-14) is a radioactive isotope which undergoes beta minus (β–) decay to the stable isotope nitrogen-14 (N-14). Energy is released during this decay. Explain why the mass of a C-14 nucleus and the mass of a N-14 nucleus are slightly different even though they have the same nucleon number.[2]
▶️Answer/Explanation
Markscheme
a.
charge: –1«e» or negative or K−
Negative signs required.
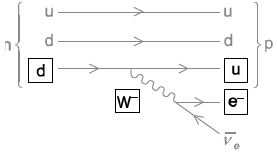
correct symbols for both missing quarks
exchange particle and electron labelled W or W– and e or e–
Do not allow W+ or e+ or β+ Allow β or β–
decay products include an electron that has mass
OR
products have energy that has a mass equivalent
OR
mass/mass defect/binding energy converted to mass/energy of decay products
«so»
mass C-14 > mass N-14
OR
mass of n > mass of p
OR
mass of d > mass of u
Accept reference to “lighter” and “heavier” in mass.
Do not accept implied comparison, eg “C-14 has greater mass”. Comparison must be explicit as stated in scheme.