IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.1 Simple harmonic motion
Topic 9 Weightage : 5 %
All Questions for Topic 9.1 – The defining equation of SHM , Energy changes
Question
Which is correct for the tangential acceleration of a simple pendulum at small amplitudes?
A It is inversely proportional to displacement.
B It is proportional to displacement.
C It is opposite to displacement.
D It is proportional and opposite to displacement.
▶️Answer/Explanation
Ans: D
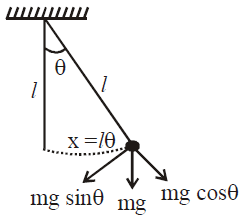
sin θ ≈ θ, so from equation (i)
Question
A simple pendulum bob oscillates as shown.
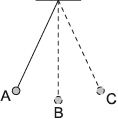
At which position is the resultant force on the pendulum bob zero?
A. At position A
B. At position B
C. At position C
D. Resultant force is never zero during the oscillation
▶️Answer/Explanation
Markscheme
D
At the equilibrium position of an oscillating pendulum, its acceleration is momentarily zero as the velocity reaches its maximum value. But this is circular motion, meaning that it must always have a resultant force towards the centre of the circle.
Question
A mass at the end of a vertical spring and a simple pendulum perform oscillations on Earth that are simple harmonic with time period T. Both the pendulum and the mass-spring system are taken to the Moon. The acceleration of free fall on the Moon is smaller than that on Earth. What is correct about the time periods of the pendulum and the mass-spring system on the Moon?
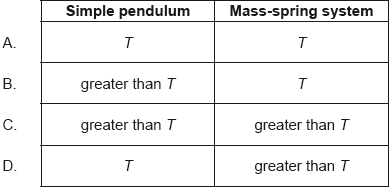
▶️Answer/Explanation
Markscheme
B
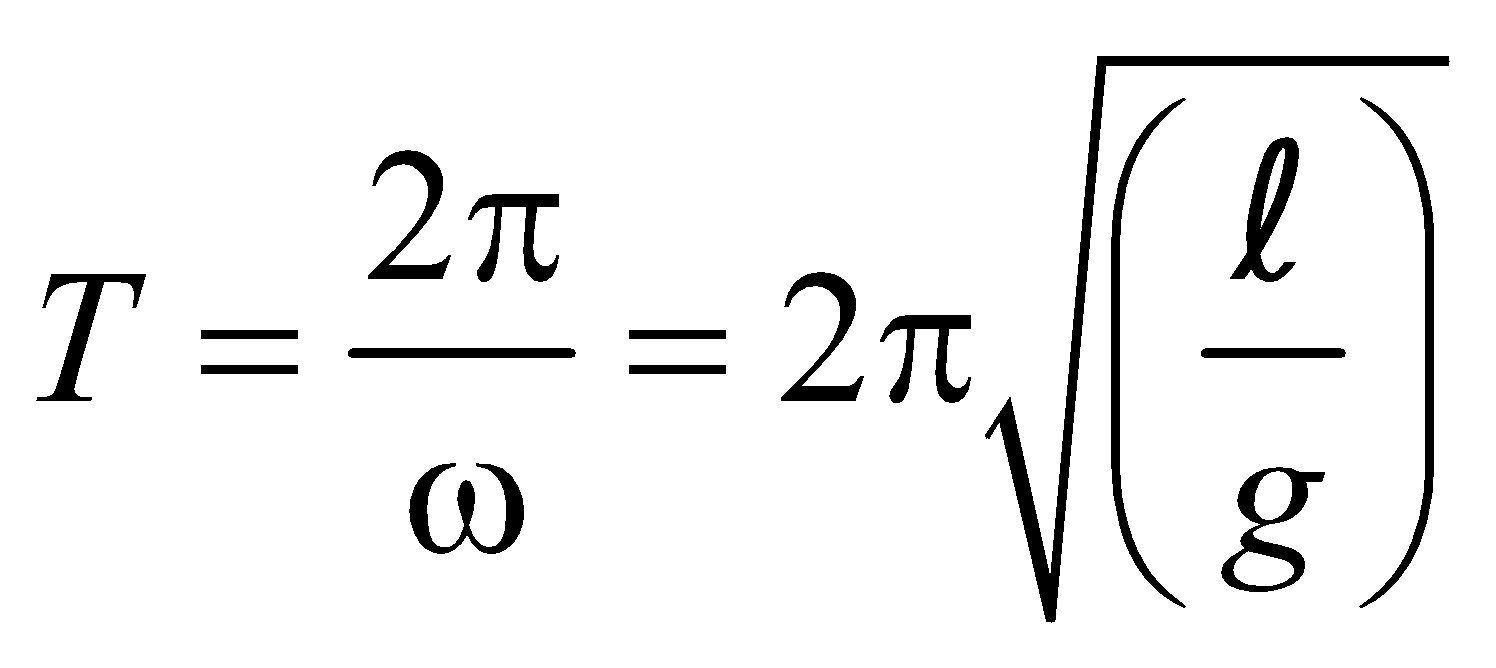
Hence g decreases means T increases
Question
A spring loaded with mass m oscillates with simple harmonic motion. The amplitude of the motion is A and the spring has total energy E. What is the total energy of the spring when the mass is increased to 3m and the amplitude is increased to 2A?
A. 2E
B. 4E
C. 12E
D. 18E
▶️Answer/Explanation
Markscheme
B
\(\Rightarrow E’ = \frac{1}{2}kA’^2 = \frac{1}{2}k 4 A^2\)
\(=4E\)
Question
A mass oscillates with simple harmonic motion (SHM) of amplitude xo. Its total energy is 16 J.
What is the kinetic energy of the mass when its displacement is \(\frac{{{x_0}}}{2}\)?
A. 4 J
B. 8 J
C. 12 J
D. 16 J
▶️Answer/Explanation
Markscheme
C
Total Energy \(= \frac{1}{2}kx_0^2\)
Kinetic Energy \(= \frac{1}{2}k(x_0^2-x^2)\)
Given \(x= \frac{x_0}{2}\)
Hence
K.E when \(x = \frac{x_0}{2} =\)
\(\frac{1}{2}k(x_0^2-x^2) =\frac{1}{2}k(x_0^2-(\frac{x_0}{2})^2)\)
\(=\frac{3}{4}(\frac{1}{2}kx_0^2) = \frac{3}{4} E\)
Also \(E= 16 \;J\)
Hence
\(K.E = \frac{3}{4}\times 16 =12 \;J\)
Question
A pendulum oscillating near the surface of the Earth swings with a time period T. What is the time period of the same pendulum near the surface of the planet Mercury where the gravitational field strength is 0.4g?
A. 0.4T
B. 0.6T
C. 1.6T
D. 2.5T
▶️Answer/Explanation
Markscheme
C
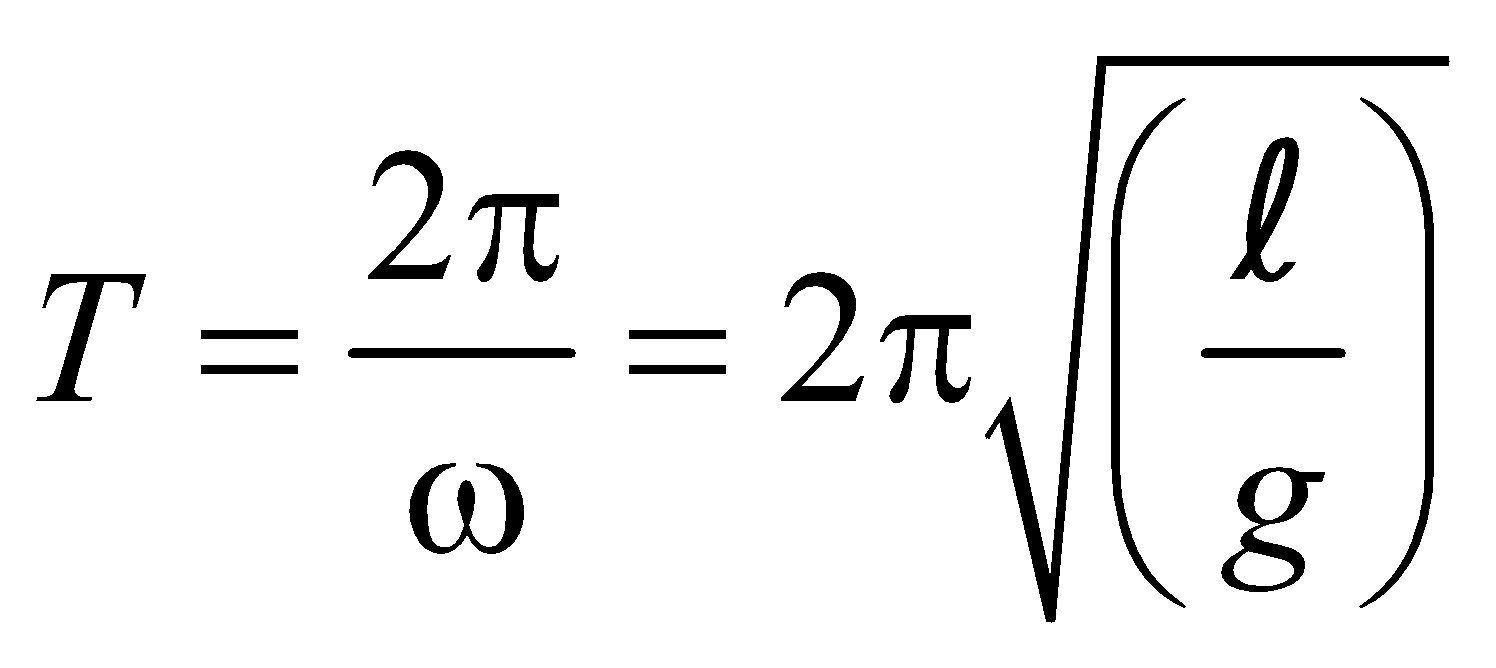
\(T_{earth}=2\pi\sqrt{\frac{l}{g_{earth}}}\)
\(T_{Merc}=2\pi\sqrt{\frac{l}{g_{Merc}}}\)
or
\(\frac{T_{Merc}}{T_{earth}}=\sqrt{\frac{g_{earth}}{g_{Merc}}}\)
\(=\sqrt{\frac{g}{0.4g}}=\sqrt{2.5}\)
\(T_{Merc}\approx 1.6T\)
Question
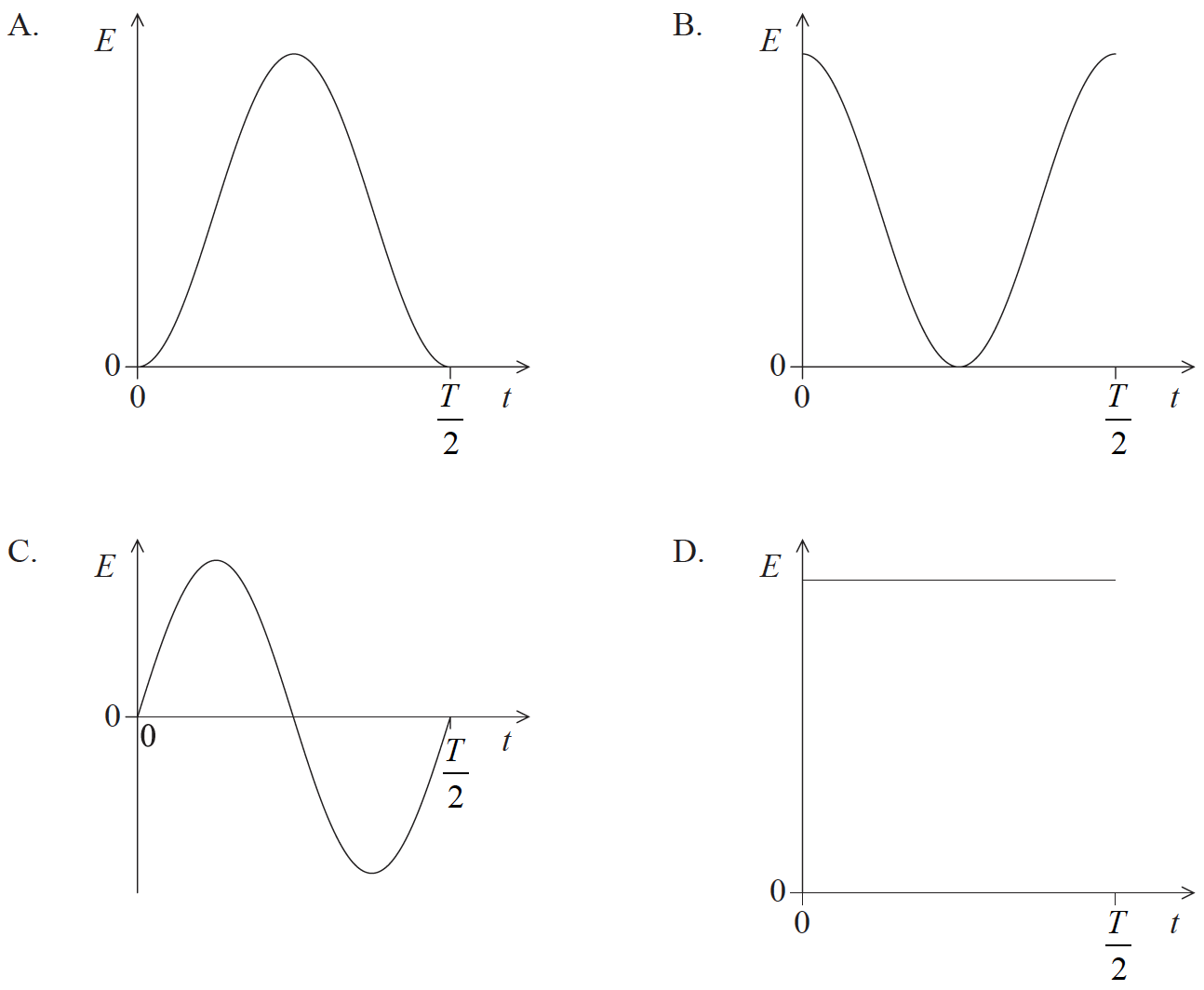
A particle executes simple harmonic motion (SHM) with period T.
Which sketch graph correctly shows how the total energy E of the particle varies with time t from t = 0 to \(t = \frac{T}{2}\)?
▶️Answer/Explanation
Markscheme
D
Total Energy is constant.
Question
A particle of mass \(m\) oscillates with simple harmonic motion (SHM) of angular frequency \(\omega \). The amplitude of the SHM is \(A\). What is the kinetic energy of the particle when it is half way between the equilibrium position and one extreme of the motion?
A. \(\frac{{m{A^2}{\omega ^2}}}{4}\)
B. \(\frac{{3m{A^2}{\omega ^2}}}{8}\)
C. \(\frac{{9m{A^2}{\omega ^2}}}{{32}}\)
D. \(\frac{{15m{A^2}{\omega ^2}}}{{32}}\)
▶️Answer/Explanation
Markscheme
B
\(\therefore K.E = \frac{1}{2}mw^2(A^2-(\frac{A}{2})^2 )\)
\(=\frac{3}{8}mw^2A^2\)
