Question
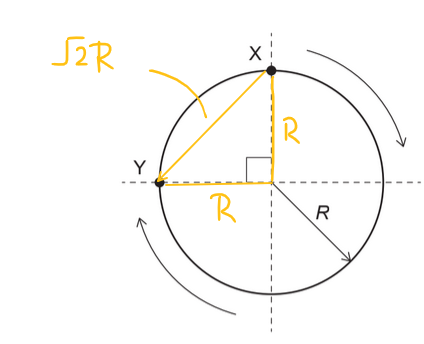
A car travels clockwise around a circular track of radius R. What is the magnitude of displacement from X to Y?
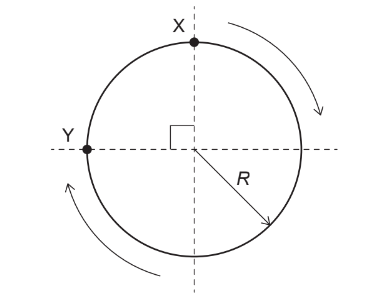
A. \( R \frac{3 \pi}{2}\)
B. \(R \frac{\pi}{2}\)
C. \(R \sqrt{2}\)
D. \(R\)
▶️Answer/Explanation
Ans:C
The displacement from point X to point Y is a chord of the circle and can be represented by the line connecting points X and Y.
Question
A stone of mass m is projected vertically upwards with speed u from the top of a cliff. The speed of the stone when it is just about to hit the ground is v.
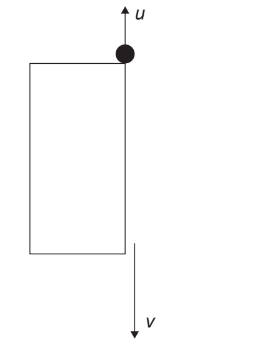
What is the magnitude of the change in momentum of the stone?
A. \(m\left(\frac{v+u}{2}\right)\)
B. \(m\left(\frac{v-u}{2}\right)\)
C. \(m(v+u)\)
D. \(m(v-u)\)
▶️Answer/Explanation
Ans:C
The initial momentum of the stone, when it is projected vertically upwards with speed \(u\), is \(+mu\) (upwards is considered positive).
The final momentum of the stone, just before it hits the ground, is \(-mv\) (downwards is considered negative).
Now, the change in momentum is:
Change in momentum = Final momentum – Initial momentum
Change in momentum = \(-mv – mu\)
Change in momentum = \(m(-v – u)\)
Change in momentum = \(m(-(v + u))\)
So, the magnitude of the change in momentum is:
\(|m(v + u)|\)
Question
A car accelerates uniformly. The car passes point \(X\) at time \(t_1\) with velocity \(v_1\) and point \(Y\) at time \(t_2\) with velocity \(v_2\). The distance \(X Y\) is \(s\).
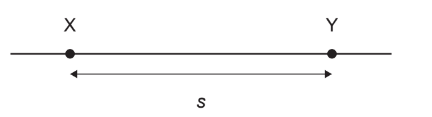
The following expressions are proposed for the magnitude of its acceleration a:
I. \(a=\frac{2 s}{\left(t_2-t_1\right)^2}\)
II. \(a=\frac{v_2^2-v_1^2}{2 s}\)
III. \(a=\frac{v_2-v_1}{t_2-t_1}\)
Which is correct?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Ans:C
To determine which expressions for the magnitude of acceleration (\(a\)) are correct, we can analyze each of the proposed expressions one by one:
I. \(a = \frac{2s}{(t_2 – t_1)^2}\)
Expression I is incorrect because it assumes that the initial velocity \(\left(v_1\right)\) is zero, which may not be the case for the uniformly accelerating car.
II. \(a = \frac{v_2^2 – v_1^2}{2s}\)
This expression is also correct. It’s derived from the kinematic equation for uniformly accelerated motion: \(v^2 = u^2 + 2as\), where \(v_2\) is the final velocity, \(v_1\) is the initial velocity, \(s\) is the displacement, and \(a\) is the acceleration. Solving for \(a\) results in this expression.
III. \(a = \frac{v_2 – v_1}{t_2 – t_1}\)
This expression is also correct and is derived from the definition of acceleration as the rate of change of velocity over time.
So, expressions (II, and III) are correct.
Question
An object is travelling with velocity \(5 \mathrm{~ms}^{-1}\). The object then accelerates to \(15 \mathrm{~ms}^{-1}\) in the same direction.
What is the variation with time of the acceleration of the object?
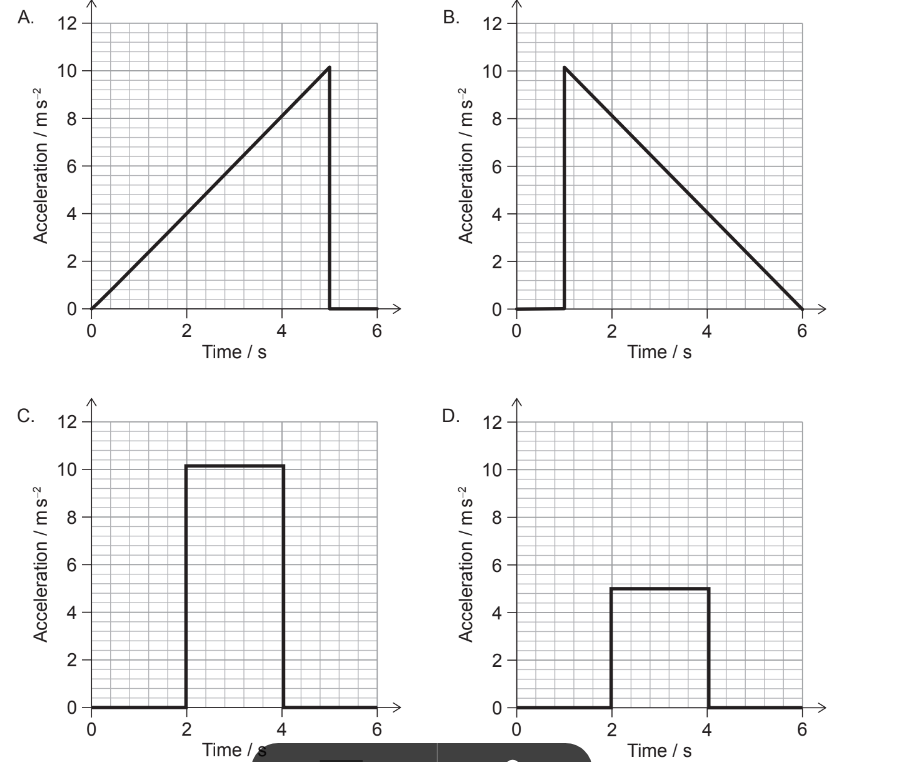
▶️Answer/Explanation
Ans:D
\(\begin{aligned} &a=\frac{d {v}}{d t} \\ & \int a d t=\Delta v \\ & \begin{aligned} \text { Area under graph } & =\text { Change of velocity } \\ & =15-5 \\ & =10 \mathrm{~ms}^{-1}\end{aligned}\end{aligned}\)
Area in graph D,
base $\times $ altitude $= 5\times 2 =10~ m/s$
Question
A rocket travels a distance of \(3 \mathrm{~km}\) in \(10 \mathrm{~s}\).
What is the order of magnitude of \(\frac{\text { the speed of the rocket }}{\text { the speed of light in a vacuum }} ?\)
A. -5
B. -6
C. -7
D. -8
▶️Answer/Explanation
Ans:B
\(\begin{aligned} & v=\frac{3000}{10} =3\times 10^2 \\ & \begin{aligned} \frac{v}{c} & =\frac{3 \times 10^2 \mathrm{~m/s}}{3 \times 10^8m/s} \\ & =1 \times(10^{-6}) \end{aligned}\end{aligned}\)