Question
A uniform ladder of weight 50.0 N and length 4.00 m is placed against a frictionless wall making an angle of 60.0° with the ground.
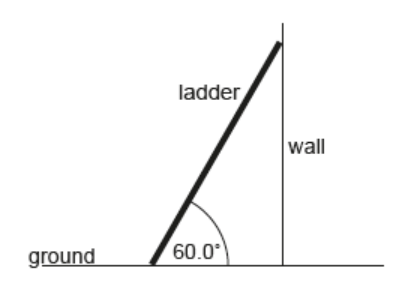
a. Outline why the normal force acting on the ladder at the point of contact with the wall is equal to the frictional force $F$ between the ladder and the
ground.[1]
b. Calculate $F$.[2]
c. The coefficient of friction between the ladder and the ground is 0.400 . Determine whether the ladder will slip.[2]
▶️Answer/Explanation
Ans:
a. «translational equilibrium demands that the» resultant force in the horizontal direction must be zeror
«hence $N_{\mathrm{W}}=F_»$
Equality of forces is given, look for reason why.
b. «clockwise moments = anticlockwise moments»
$
\begin{aligned}
& 50 \times 2 \cos 60=N_{\mathrm{W}} \times 4 \sin 60 \checkmark \\
& « \mathrm{~N}_{\mathrm{W}}=\mathrm{F}=\frac{50 \times 2 \cos 60}{4 \sin 60} » \\
& F=14.4 « N »
\end{aligned}
$
c. maximum friction force $=« 0.4 \times 50 \mathrm{~N} »=20 \ll \mathrm{N} »$
$14.4<20$ AND so will not slip
Question
The moment of inertia of a solid sphere is $I=\frac{2}{5} m r^2$ where $m$ is the mass of the sphere and $r$ is the radius.
a. Show that the total kinetic energy $E_{\mathrm{k}}$ of the sphere when it rolls, without slipping, at speed $v$ is $E_{\mathrm{K}}=\frac{7}{10} m v^2$. [2]
b. A solid sphere of mass $1.5 \mathrm{~kg}$ is rolling, without slipping, on a horizontal surface with a speed of $0.50 \mathrm{~m} \mathrm{~s}^{-1}$. The sphere then rolls, without
slipping, down a ramp to reach a horizontal surface that is $45 \mathrm{~cm}$ lower.[3]

Calculate the speed of the sphere at the bottom of the ramp
▶️Answer/Explanation
Ans:
a. $E_{\mathrm{k}}=E_{\mathrm{k}}$ linear $+E_{\mathrm{k}}$ rotational
OR
$
\begin{aligned}
& E_{\mathrm{k}}=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2 \checkmark \\
& =\frac{1}{2} m v^2+\frac{1}{2} \times \frac{2}{5} m r^2 \times\left(\frac{v}{r}\right)^2 \checkmark \\
& «=\frac{7}{10} m v^2 »
\end{aligned}
$
Answer is given in the question so check working is correct at each stage.
b. Initial $E_K=\frac{7}{10} \times 1.50 \times 0.5^2 «=0.26 \mathrm{~J} »$
Final $E_K=0.26+1.5 \times 9.81 \times 0.45 \ll=6.88 \mathrm{~J} »$
$
v=« \sqrt{\frac{10}{7} \times \frac{6.88}{1.5}}=» 2.56\left\langle\mathrm{~m} \mathrm{~s}^{-1} » \vee\right.
$
Other solution methods are possible.