Question
The escape speed from the surface of earth is \(v_{\mathrm{esc}}\). The radius of earth is \(R\). A satellite of mass \(m\) is in orbit at a height \(\frac{R}{4}\) above the surface of the Earth. What is the energy required to move the satellite to infinity?
A. \(\frac{m v_{\text {esc }}^2}{5}\)
B. \(\frac{2 m v_{\text {esc }}^2}{5}\)
C. \(m v_{\text {esc }}^2\)
D. \(2 m v_{\text {esc }}^2\)
▶️Answer/Explanation
Ans:A
To calculate the energy required to move the satellite from its orbit at a height of \(R/4\) above the surface of the Earth to infinity, you need to consider both the gravitational potential energy and the kinetic energy.
The initial gravitational potential energy of the satellite at a height \(R/4\) above the surface of the Earth is given by:
\[U_{\text{initial}} = -\frac{GMm}{R + \frac{R}{4}}\]
The negative sign indicates that this is the gravitational potential energy, and it is negative because it is measured relative to infinity.
The satellite is in orbit, so its kinetic energy is given by:
\[K = \frac{1}{2}mv^2\]
Where \(v\) is the orbital velocity at that height. The orbital velocity at a height \(h\) above the Earth’s surface is given by:
\[v = \sqrt{\frac{GM}{R + h}}\]
So, the kinetic energy at the initial position is:
\[K_{\text{initial}} = \frac{1}{2}m\left(\sqrt{\frac{GM}{R + \frac{R}{4}}}\right)^2\]
Now, let’s calculate the final potential energy at infinity. As the satellite moves to infinity, the gravitational potential energy approaches zero, and the kinetic energy also becomes zero. Therefore, the final energy at infinity is zero.
So, the energy required to move the satellite to infinity is the difference between the initial energy and the final energy:
\[E_{\text{required}} = U_{\text{initial}} + K_{\text{initial}} – 0\]
Substitute the expressions for \(U_{\text{initial}}\) and \(K_{\text{initial}}\):
\[E_{\text{required}} = -\frac{GMm}{R + \frac{R}{4}} + \frac{1}{2}m\left(\sqrt{\frac{GM}{R + \frac{R}{4}}}\right)^2\]
Simplify the expression:
\[E_{\text{required}} = -\frac{GMm}{\frac{5R}{4}} + \frac{1}{2}m\left(\frac{\sqrt{\frac{GM}{R + \frac{R}{4}}}}{1}\right)^2\]
Now, calculate the energy required:
\[E_{\text{required}} = -\frac{4GMm}{5R} + \frac{1}{2}m\left(\frac{\sqrt{\frac{GM}{R + \frac{R}{4}}}}{1}\right)^2\]
Simplify further:
\[E_{\text{required}} = -\frac{4GMm}{5R} + \frac{1}{2}m\left(\sqrt{\frac{GM}{R + \frac{R}{4}}}\right)^2\]
\[E_{\text{required}} = -\frac{4GMm}{5R} + \frac{1}{2}m\frac{GM}{R + \frac{R}{4}}\Rightarrow |m\times \frac{2GM}{5R}|\]
\[V_{esc}=\sqrt{\frac{2 G M}{R}}\]
So from this \[E_{\text{required}} =\frac{m v_{\text {esc }}^2}{5}\]
Question
Two isolated point masses, P of mass m and Q of mass 2m, are separated by a distance 3d. X is a point a distance d from P and 2d from Q.

What is the net gravitational field strength at X and the net gravitational potential at X?

▶️Answer/Explanation
Ans:D
To find the net gravitational field strength and potential at point X due to the two masses, you can use the principles of superposition for gravitational fields and potentials.
Gravitational Field Strength at X (g_X):
The gravitational field strength at a point due to a single point mass is given by:
\[g = \frac{GM}{r^2},\]
Let’s calculate the field strength at X due to each of the masses:
- For mass P (m), the distance from P to X is \(d\), so the field strength at X due to P is \(g_P = \frac{Gm}{d^2}\).
- For mass Q (2m), the distance from Q to X is \(2d\), so the field strength at X due to Q is \(g_Q = \frac{G(2m)}{(2d)^2} = \frac{Gm}{2d^2}\).
Since these field strengths are in opposite directions (toward P and away from Q), you need to subtract them to find the net field strength at X:
\[g_X = g_P – g_Q = \frac{Gm}{d^2} – \frac{Gm}{2d^2} = \frac{Gm}{2d^2}.\]
Gravitational Potential at X (V_X):
The gravitational potential at a point due to a single point mass is given by:
\[V = -\frac{GM}{r},\]
where the negative sign indicates that the potential decreases with increasing distance from the mass.
Let’s calculate the potential at X due to each of the masses:
- For mass P (m), the potential at X due to P is \(V_P = -\frac{Gm}{d}\).
- For mass Q (2m), the potential at X due to Q is \(V_Q = -\frac{G(2m)}{2d} = -\frac{Gm}{d}.\)
Again, since these potentials are in opposite directions, you need to add them to find the net potential at X:
\[V_X = V_P + V_Q = -\frac{Gm}{d} – \frac{Gm}{d} = -\frac{2Gm}{d}.\]
So, the net gravitational field strength at point X is \(\frac{3Gm}{4d^2}\), and the net gravitational potential at point X is \(-\frac{2Gm}{d}\).
Question
The mass of Mars is about ten times that of the Moon. The radius of Mars is about twice that of the Moon.
What is the \(\frac{\text { escape speed from Mars }}{\text { escape speed from Moon }}\) ?
A. \(\sqrt{5}\)
B. \(2 \sqrt{5}\)
C. 5
D. 25
▶️Answer/Explanation
Ans:A
\[
V_{\text {esc-moon }}=\sqrt{\frac{2 G M}{R}}
\]
\(\therefore\) For mars \(V_{\text {esc-mars }}=\sqrt{\frac{2 G \times 10 M}{2 R}}\)
\[
=\sqrt{2 \frac{G M}{R} \cdot 5}\Rightarrow V_{\text {esc-mars }}=\sqrt{5 }\cdot V_{\text {esc-moon }}
\]
Question
The gravitational field strength at the surface of the Earth is often taken to be \(9.8 \mathrm{Nkg}^{-1}\).
The use of this value to calculate the weight of an object above the surface of the Earth is
A. a paradigm shift in our understanding of gravity.
B. an attempt to model gravitational fields.
C. an outcome from a peer review.
D. an approximation used for estimation purposes.
▶️Answer/Explanation
Ans:D
D. an approximation used for estimation purposes.
The use of \(9.8 \, \text{Nkg}^{-1}\) (approximately 9.8 m/s²) as the gravitational field strength at the surface of the Earth is a common approximation for estimation purposes. It simplifies calculations and provides a reasonable approximation for most everyday scenarios. However, it is not a paradigm shift, an attempt to model gravitational fields, or an outcome from a peer review. It is a practical value used to make calculations involving weight and gravity more manageable in common situations.
Question
Four uniform planets have masses and radii as shown. Which planet has the smallest escape speed?
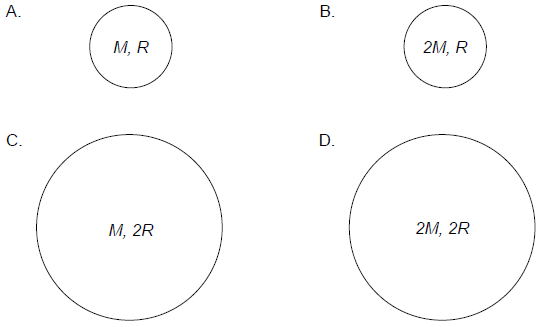
Answer/Explanation
Markscheme
C
Escape velocity is given by
\(v_e=\sqrt{\frac{2GM_p}{R_p}}\)
For smallest \(v_e , M_p \) should be small and \(R_p \) should be big
\(\frac{M_p}{R_p}\)
for \(A = 1\) , For \(B =2\) , for \(C = \frac{1}{2} \) and for \(D =1\)
Hence C will have least escape velocity