Question
A negatively charged particle is stationary halfway between two horizontal charged plates. The plates are separated by a distance d with potential difference V between them.

What is the magnitude of the electric field and direction of the electric field at the position of the particle?

▶️Answer/Explanation
Ans:D
\(\begin{gathered}E=-\frac{d V}{d r}=\frac{V}{d} \\ E=U / d\end{gathered}\)
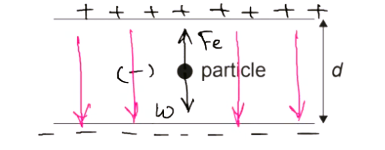
As negative charge is stationary it means the weight must be balanced by Electric Force.
Which means Electric force will act upward direction as weight act downward.
From this \( \overrightarrow{F_e}=q \vec{E} \) we can conclude Electric field have opposite direction due to negative charge.
Electric field will direction will be down.
Question
P and R are parallel wires carrying the same current into the plane of the paper. P and R are equidistant from a point Q. The line PQ is perpendicular to the line RQ.

The magnetic field due to \(P\) at \(Q\) is \(X\). What is the magnitude of the resultant magnetic field at \(Q\) due to both wires?
A. \(\frac{x}{2}\)
B. \(x\)
C. \(x \sqrt{2}\)
D. \(2 x\)
▶️Answer/Explanation
Ans:C
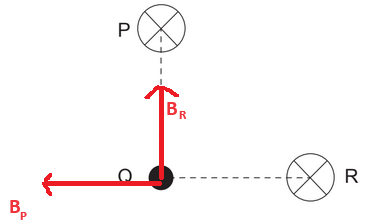
$B_{eq}=\sqrt{x^2+x^2}\Rightarrow x\sqrt{x}$
Question
Two positive charges of magnitude \(q\) and \(2 q\) are fixed as shown. At which position is the electric field, due to these charges, equal to zero?

▶️Answer/Explanation
Ans:B
At position A and D electric can never be zero.

At B distance from 2q is much more then c and magnitude is also 2 times so more possibility of cancel out each other because At C distance from q is lower and magnitude is also smaller in compare to 2q so there is more chance that $E_2q$ will ore domniate over $E_q$
Question
Three point charges, \(+Q,+Q\) and \(-Q\), are fixed at the three corners of a square. What is the direction of the electric field at the fourth corner?

▶️Answer/Explanation
Ans:B

Question
Two spheres have the same positive charge. A point M is midway between the two spheres.
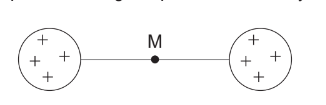
Along the line joining the spheres, what is true about the electrical field and the electric potential at M?

▶️Answer/Explanation
Ans:A
The electric field (\(E\)) at point \(M\), which is midway between two spheres with the same positive charge, will be zero. This is because the electric fields generated by each sphere will be equal in magnitude and opposite in direction, canceling each other out at the midpoint.
On the other hand, the electric potential (\(V\)) at point \(M\) will be the minimum positive value. This is because the electric potential due to a single positive charge is always a positive value, and the potential due to both spheres at point \(M\) will be the sum of their individual potentials, resulting in the minimum positive value.
So, the correct combination is:
Electric field: zero
Electric potential: minimum positive value