Question
Nature of science:
Pure science: Einstein based his theory of relativity on two postulates and deduced the rest by mathematical analysis. The first postulate integrates all of the laws of physics including the laws of electromagnetism, not only Newton’s laws of mechanics. (1.2)
Understandings:
The two postulates of special relativity
Clock synchronization
The Lorentz transformations
Velocity addition
Invariant quantities (spacetime interval, proper time, proper length and rest mass)
Time dilation
Length contraction
The muon decay experiment
Applications and skills:
Using the Lorentz transformations to describe how different measurements of space and time by two observers can be converted into the measurements observed in either frame of reference
Using the Lorentz transformation equations to determine the position and time coordinates of various events
Using the Lorentz transformation equations to show that if two events are simultaneous for one observer but happen at different points in space, then the events are not simultaneous for an observer in a different reference frame
Solving problems involving velocity addition
Deriving the time dilation and length contraction equations using the Lorentz equations
Solving problems involving time dilation and length contraction
Solving problems involving the muon decay experiment
Guidance:
Problems will be limited to one dimension
Derivation of the Lorentz transformation equations will not be examined
Muon decay experiments can be used as evidence for both time dilation and length contraction
Data booklet reference:
- $\gamma=\frac{1}{\sqrt{1-\frac{v^2}{e^2}}}$
- $x^{\prime}=\gamma(x-v t) ; \Delta x^{\prime}=\gamma(\Delta x-v \Delta t)$
- $t^{\prime}=\gamma\left(t-\frac{v x}{c^2}\right) ; \Delta t^{\prime}=\gamma\left(\Delta t-\frac{v \Delta x}{c^2}\right)$
- $\boldsymbol{u}^{\prime}=\frac{u-v}{1-\frac{\mathrm{vw}}{e^2}} \mid$
- $\Delta t=\gamma \Delta t_0$
- $L=\frac{L_0}{\gamma}$
- $\left(c t^{\prime}\right)^2-\left(x^{\prime}\right)^2=(c t)^2-(x)^2$
Utilization:
- Once a very esoteric part of physics, relativity ideas about space and time are needed in order to produce accurate global positioning systems (GPS)
Aims:
- Aim 2: the Lorentz transformation formulae provide a consistent body of knowledge that can be used to compare the description of motion by one observer to the description of another observer in relative motion to the first
- Aim 3: these formulae can be applied to a varied set of conditions and situations
- Aim 9: the introduction of relativity pushed the limits of Galilean thoughts on space and motion
Question
A train is moving across a bridge with a speed $v=0.40 c$. Observer $A$ is at rest in the train. Observer $B$ is at rest with respect to the bridge.
The length of the bridge $L_B$ according to observer $B$ is $2.0 \mathrm{~km}$.
According to observer $\mathrm{B}$, two lamps at opposite ends of the bridge are turned on simultaneously as observer A crosses the bridge. Event $\mathrm{X}$ is the lamp at one end of the bridge turning on. Event $Y$ is the lamp at the other end of the bridge turning on.
Events X and Y are shown on the spacetime diagram. The space and time axes of the reference frame for observer B are x and ct. The line labelled ct’ is the worldline of observer A.
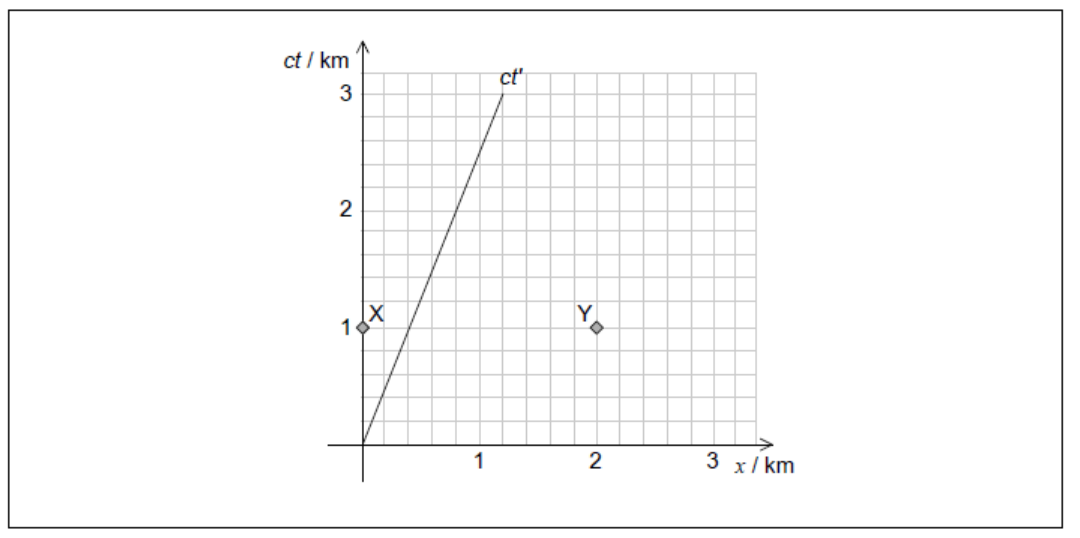
a(i)Calculate, for observer $A$, the length $L_A$ of the bridge[2]
a(ii)Calculate, for observer $A$, the time taken to cross the bridge.[2]
b. Outline why $L_B$ is the proper length of the bridge.[1]
c(i)Draw, on the spacetime diagram, the space axis for the reference frame of observer A. Label this axis $x^{\prime}$.[1]
c(ii)Demonstrate using the diagram which lamp, according to observer $\mathrm{A}$, was turned on first.[2]
c(iii)Demonstrate, using the diagram, which lamp observer A observes to light first.[2]
c(iv)Determine the time, according to observer $\mathrm{A}$, between $\mathrm{X}$ and $\mathrm{Y}$.[2]
▶️Answer/Explanation
Ans:
$
\begin{aligned}
& \mathrm{a}(\mathrm{i}) \gamma=1.09 \\
& L_{\mathrm{A}}=« \frac{2.0}{1.09}=» 1.8 « \mathrm{~km} »
\end{aligned}
$
a(ii)ALTERNATIVE 1
$
\begin{aligned}
& \text { time }=\frac{1.8 \times 10^3}{1.2 \times 10^8} \\
& 1.5 \times 10^{-5} « s »
\end{aligned}
$
ALTERNATIVE 2
$
\begin{aligned}
t_B & =\frac{2 \times 10^3}{1.2 \times 10^8}=1.66 \times 10^{-5} \text { 《S》 } \\
t_{\mathrm{A}} & =\frac{t_{\mathrm{B}}}{\gamma}=1.5 \times 10^{-5} \text { «S》 }
\end{aligned}
$
b. $L_B$ is the length/measurement «by observer $B$ » made in the reference frame in which the bridge is at rest
NOTE: Idea of rest frame or frame in which bridge is not moving is required.
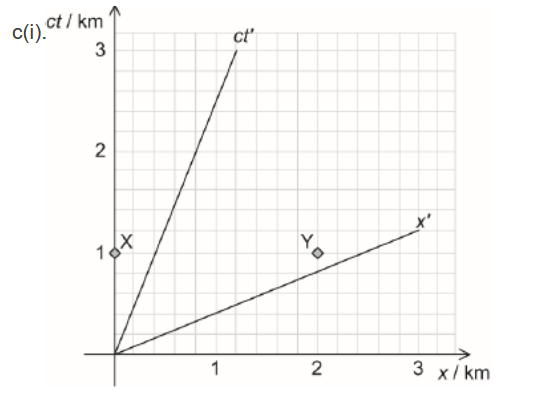
x′ axis drawn with correct gradient of 0.4 ✔
NOTE: Line must be 1 square below Y, allow ±0.5 square.
Allow line drawn without a ruler.
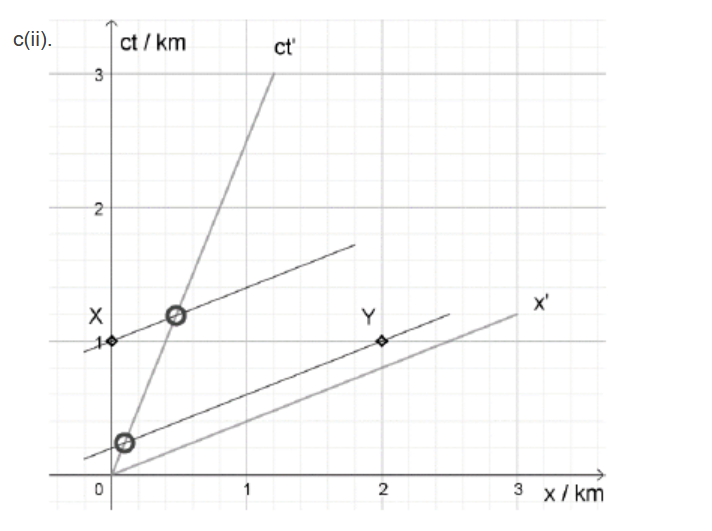
lines parallel to the x′ axis through X and Y intersecting the worldline ct′ at points shown ✔
so Y/lamp at the end of the bridge turned on first ✔
NOTE: Allow lines drawn without a ruler
Do not allow MP2 without supporting argument or correct diagram.
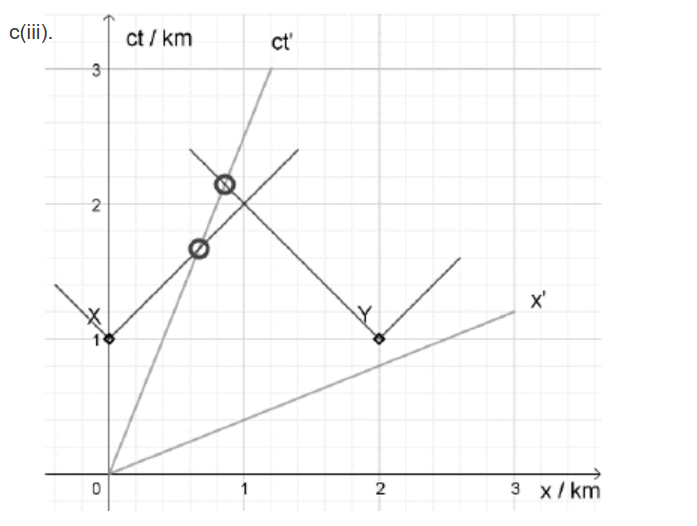
light worldlines at 45° from X AND Y intersecting the worldline ct′ ✔
so light from lamp X is observed first ✔
NOTE: Allow lines drawn without a ruler.
Do not allow MP2 without supporting argument or correct diagram.
ALTERNATIVE 1
$
\begin{aligned}
& \Delta t^{\prime}=1.09 \times\left(0-\frac{0.4 \times 2.0 \times 10^3}{3.0 \times 10^8}\right) \\
& =«-» 2.9 \times 10^{-6} \text { «s» }
\end{aligned}
$
ALTERNATIVE 2
equating spacetime intervals between $X$ and $Y$
relies on realization that $\Delta x^{\prime}=\gamma(\Delta x-0)$ eg:
$\left(c \Delta t^{\prime}\right)^2-(1.09 \times 2000)^2=0^2-2000^2$
$
\Delta t^{\prime}=\left\langle \pm \gg \frac{\sqrt{(1.09 \times 2000)^2-2000^2}}{3.0 \times 10^8}=\left\langle \pm » 2.9 \times 10^{-6} \ll \mathrm{S} \gg\right.\right.
$
ALTERNATIVE 3
use of diagram from answer to $4(\mathrm{c})(\mathrm{ii})(1$ small square $=200 \mathrm{~m}$ ) counts 4.5 to 5 small squares (allow $900-1000 \mathrm{~m}$ ) between events for A seen on B’s $c t$ axis $\frac{950}{\gamma c}=2.9 \times 10^{-6} \pm 0.2 \times 10^{-6} \ll \mathrm{S} \gg$