Question
A train is moving across a bridge with a speed $v=0.40 c$. Observer $A$ is at rest in the train. Observer $B$ is at rest with respect to the bridge.
The length of the bridge $L_B$ according to observer $B$ is $2.0 \mathrm{~km}$.
According to observer $\mathrm{B}$, two lamps at opposite ends of the bridge are turned on simultaneously as observer A crosses the bridge. Event $\mathrm{X}$ is the lamp at one end of the bridge turning on. Event $Y$ is the lamp at the other end of the bridge turning on.
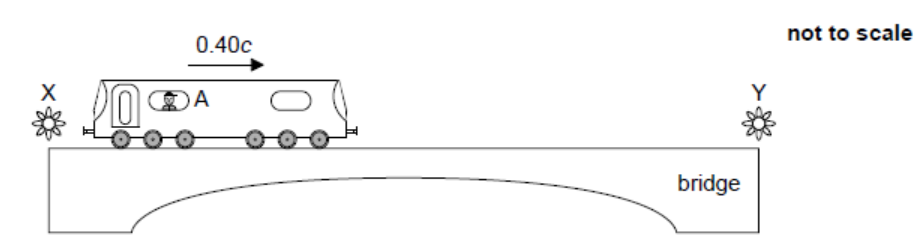
Events X and Y are shown on the spacetime diagram. The space and time axes of the reference frame for observer B are x and ct. The line labelled ct’ is the worldline of observer A.
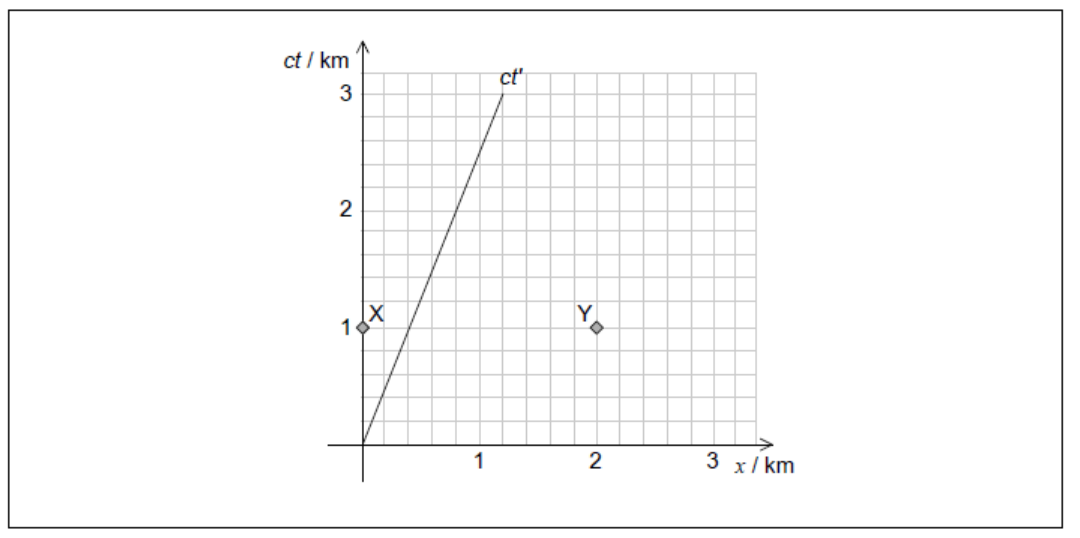
a(i)Calculate, for observer $A$, the length $L_A$ of the bridge[2]
a(ii)Calculate, for observer $A$, the time taken to cross the bridge.[2]
b. Outline why $L_B$ is the proper length of the bridge.[1]
c(i)Draw, on the spacetime diagram, the space axis for the reference frame of observer A. Label this axis $x^{\prime}$.[1]
c(ii)Demonstrate using the diagram which lamp, according to observer $\mathrm{A}$, was turned on first.[2]
c(iii)Demonstrate, using the diagram, which lamp observer A observes to light first.[2]
c(iv)Determine the time, according to observer $\mathrm{A}$, between $\mathrm{X}$ and $\mathrm{Y}$.[2]
▶️Answer/Explanation
Ans:
$
\begin{aligned}
& \mathrm{a}(\mathrm{i}) \gamma=1.09 \\
& L_{\mathrm{A}}=« \frac{2.0}{1.09}=» 1.8 « \mathrm{~km} »
\end{aligned}
$
a(ii)ALTERNATIVE 1
$
\begin{aligned}
& \text { time }=\frac{1.8 \times 10^3}{1.2 \times 10^8} \\
& 1.5 \times 10^{-5} « s »
\end{aligned}
$
ALTERNATIVE 2
$
\begin{aligned}
t_B & =\frac{2 \times 10^3}{1.2 \times 10^8}=1.66 \times 10^{-5} \text { 《S》 } \\
t_{\mathrm{A}} & =\frac{t_{\mathrm{B}}}{\gamma}=1.5 \times 10^{-5} \text { «S》 }
\end{aligned}
$
b. $L_B$ is the length/measurement «by observer $B$ » made in the reference frame in which the bridge is at rest
NOTE: Idea of rest frame or frame in which bridge is not moving is required.
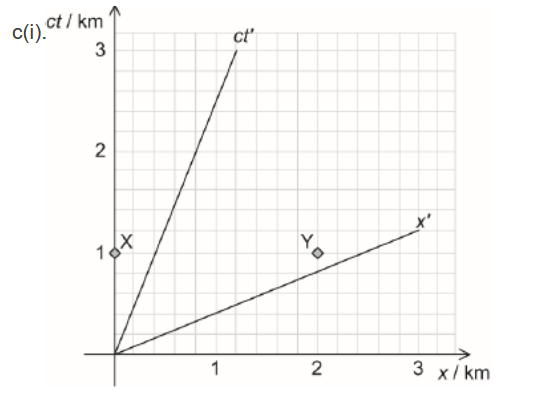
x′ axis drawn with correct gradient of 0.4 ✔
NOTE: Line must be 1 square below Y, allow ±0.5 square.
Allow line drawn without a ruler.
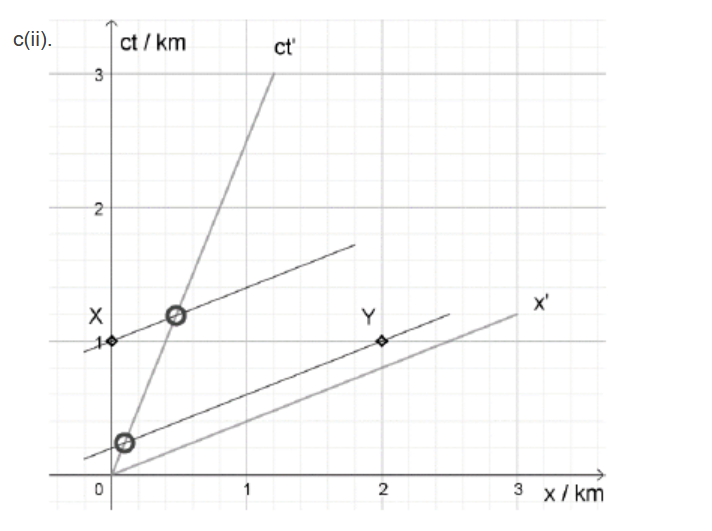
lines parallel to the x′ axis through X and Y intersecting the worldline ct′ at points shown ✔
so Y/lamp at the end of the bridge turned on first ✔
NOTE: Allow lines drawn without a ruler
Do not allow MP2 without supporting argument or correct diagram.
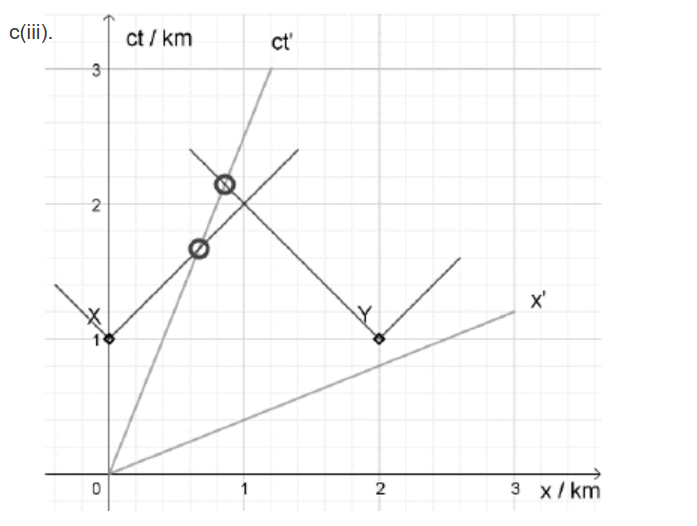
light worldlines at 45° from X AND Y intersecting the worldline ct′ ✔
so light from lamp X is observed first ✔
NOTE: Allow lines drawn without a ruler.
Do not allow MP2 without supporting argument or correct diagram.
ALTERNATIVE 1
$
\begin{aligned}
& \Delta t^{\prime}=1.09 \times\left(0-\frac{0.4 \times 2.0 \times 10^3}{3.0 \times 10^8}\right) \\
& =«-» 2.9 \times 10^{-6} \text { «s» }
\end{aligned}
$
ALTERNATIVE 2
equating spacetime intervals between $X$ and $Y$
relies on realization that $\Delta x^{\prime}=\gamma(\Delta x-0)$ eg:
$\left(c \Delta t^{\prime}\right)^2-(1.09 \times 2000)^2=0^2-2000^2$
$
\Delta t^{\prime}=\left\langle \pm \gg \frac{\sqrt{(1.09 \times 2000)^2-2000^2}}{3.0 \times 10^8}=\left\langle \pm » 2.9 \times 10^{-6} \ll \mathrm{S} \gg\right.\right.
$
ALTERNATIVE 3
use of diagram from answer to $4(\mathrm{c})(\mathrm{ii})(1$ small square $=200 \mathrm{~m}$ ) counts 4.5 to 5 small squares (allow $900-1000 \mathrm{~m}$ ) between events for A seen on B’s $c t$ axis $\frac{950}{\gamma c}=2.9 \times 10^{-6} \pm 0.2 \times 10^{-6} \ll \mathrm{S} \gg$
Question
The diagram shows space and time axes x and ct for an observer at rest with respect to a galaxy. A spacecraft moving through the galaxy has space and time axes x′ and ct
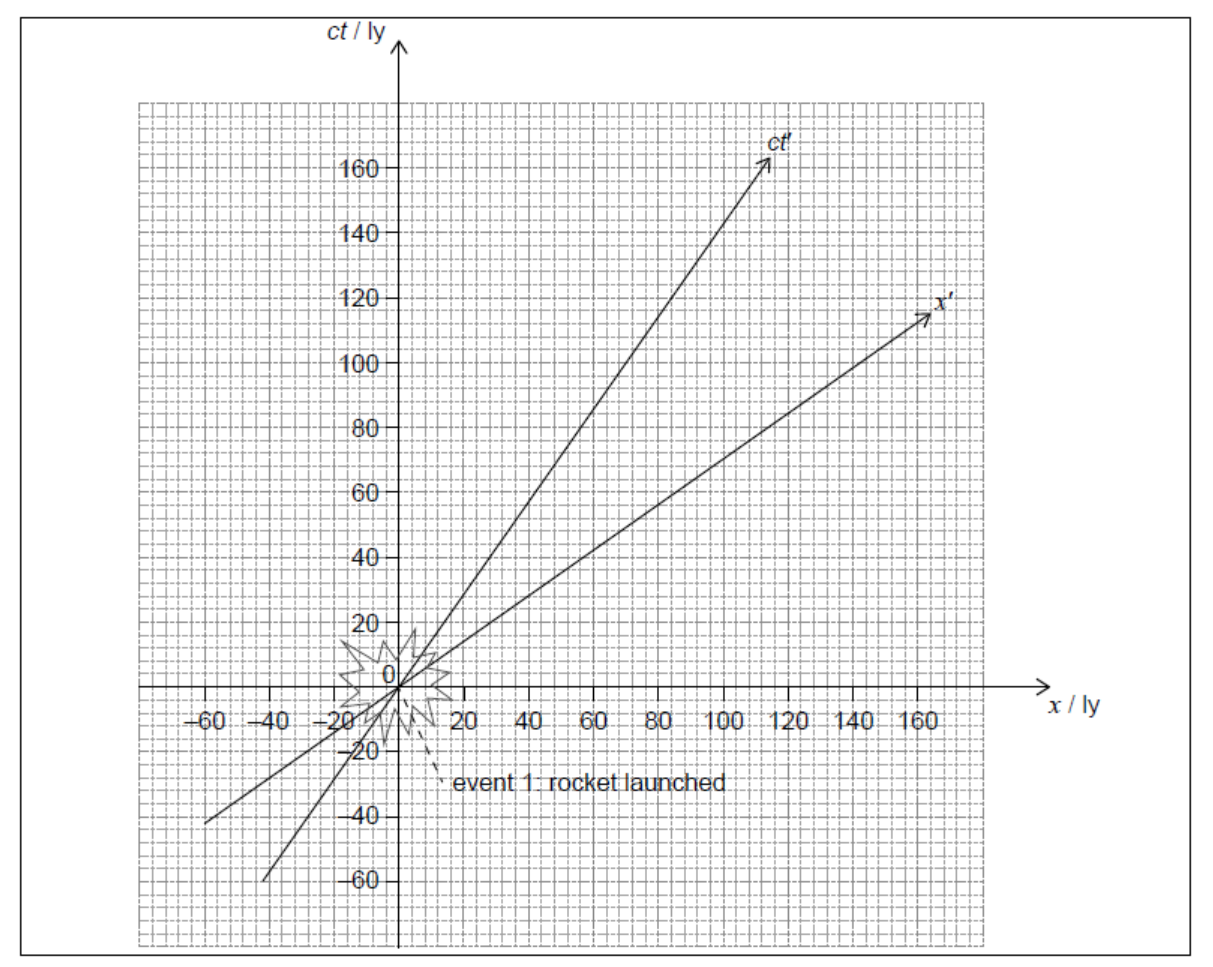
A rocket is launched towards the right from the spacecraft when it is at the origin of the axes. This is labelled event 1 on the spacetime diagram. Event 2 is an asteroid exploding at $\mathrm{x}=100 \mathrm{ly}$ and $c t=20 \mathrm{ly}$.
a. Plot, on the axes, the point corresponding to event 2 .
b. Suggest whether the rocket launched by the spacecraft might be the cause of the explosion of the asteroid.
c. Show that the value of the invariant spacetime interval between events 1 and 2 is $9600 \mathrm{ly}^2$.
d.i. An observer in the spacecraft measures that events 1 and 2 are a distance of 120 ly apart. Determine, according to the spacecraft observer, the time between events 1 and 2.[2]
d.ii.Using the spacetime diagram, determine which event occurred first for the spacecraft observer, event 1 or event 2.[2]
e. Determine, using the diagram, the speed of the spacecraft relative to the galaxy.[2]
▶️Answer/Explanation
Ans:
a.
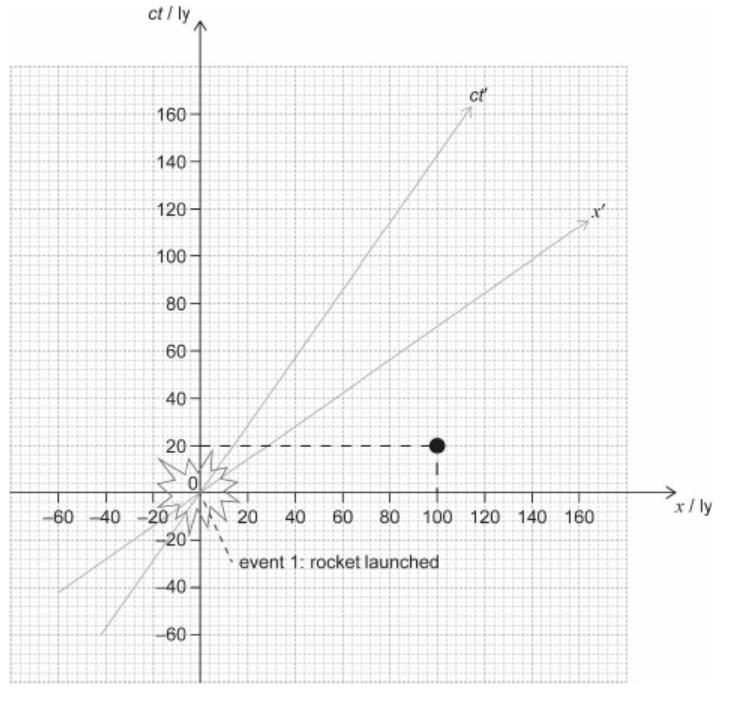
point as shown ✔
a.
b.ALTERNATIVE 1
the rocket would have to travel faster than the speed of light ✔
so impossible ✔
ALTERNATIVE 2
drawing of future lightcone at origin ✔
and seeing that the asteroid explodes outside the lightcone so impossible ✔
ALTERNATIVE 3
the event was observed at +20 years, but its distance (stationary) is 100 ly ✔
so the asteroid event happened 80 years before t = 0 for the galactic observer ✔
c. $100^2-20^2=9600 « l y^2 »$
Also accept 98 (the square root of 9600).
Allow negative value.
d.i. $9600=120^2-c^2 t^2$
$c t=«-» 69.3$ «y»/ $t=«-» 69.3$ «y»
Allow approach with Lorentz transformation.
d.iiline from event 2 parallel to $\mathrm{x}$ ‘ axis intersects $c t$ axis at a negative value event 2 occurred first
e. use of $\tan \theta=\frac{v}{c}$ with the angle between the time axes to get $(0.70 \pm 0.02) c$