Question
A black hole has a Schwarzschild radius $R$. A probe at a distance of $0.5 R$ from the event horizon of the black hole emits radio waves of frequency $f$ that are received by an observer very far from the black hole.
a. Explain why the frequency of the radio waves detected by the observer is lower than $f$. [2]
b. The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as
measured by the observer.[2]
▶️Answer/Explanation
Ans:
a. ALTERNATIVE 1
as the photons move away from the black hole, they lose energy in the gravitational field
since $E=h f$ «the detected frequency is lower than the emitted frequency»
ALTERNATIVE 2
if the observer was accelerating away from the probe, radio waves would undergo Doppler shift towards lower frequency by the equivalence principle, the gravitational field has the same effect as acceleration
ALTERNATIVE 3
due to gravitational time dilation, time between arrivals of wavefronts is greater for the observer since $f=\frac{1}{T}$, «the detected frequency is lower than the emitted frequency»
NOTE: The question states that received frequency is lower so take care not to award a mark for simply re-stating this, a valid explanation must be given.
b. time between pulses $=3 \mathrm{~s}$ according to the probe
$
\Delta t=\ll \frac{3}{\sqrt{1-\frac{1}{1.5}}}=» 5.2 \text { « } » \checkmark
$
Question
A rocket is accelerating upwards at $9.8 \mathrm{~m} \mathrm{~s}^{-2}$ in deep space. A photon of energy $14.4 \mathrm{keV}$ is emitted upwards from the bottom of the rocket and travels to a detector in the tip of the rocket $52.0 \mathrm{~m}$ above.
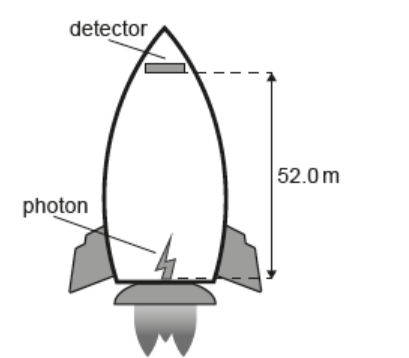
a. Explain why a change in frequency is expected for the photon detected at the top of the rocket.[3]
b. Calculate the frequency change.[2]
▶️Answer/Explanation
Ans:
a. ALTERNATIVE 1
detector accelerates/moves away from point of photon emission
so Doppler effect / redshift
so $f$ decreases
ALTERNATIVE 2
equivalent to stationary rocket on earth’s surface
photons lose «gravitational» energy as they move upwards
$\mathrm{h} f$ OR $f$ decreases
b. «Using $E=h f » f=\frac{14.4 \times 10^3 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}}=3.48 \times 10^{18}$ «z» $\checkmark$
$
\begin{aligned}
& \| \Delta f=f \frac{g \Delta h}{c^2} » \\
& \Delta f=3.48 \times 10^{18} \frac{9.81 \times 52}{\left(3 \times 10^8\right)^2}=1.97 \times 10^4 \text { «z » } \quad
\end{aligned}
$