Question
A Pitot tube shown in the diagram is used to determine the speed of air flowing steadily in a horizontal wind tunnel. The narrow tube between points A and B is filled with a liquid. At point B the speed of the air is zero.
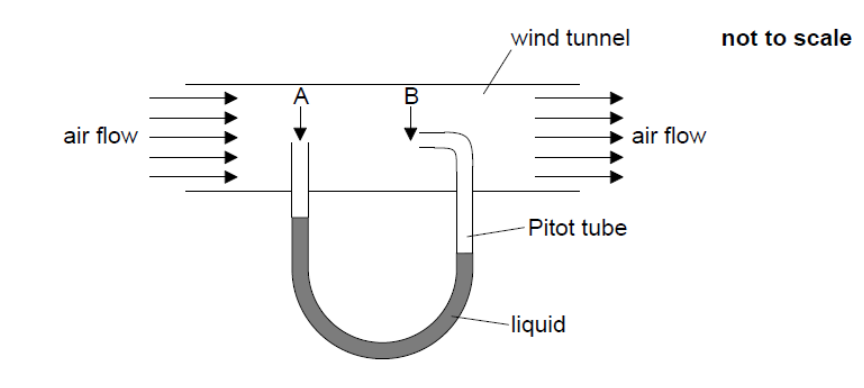
a. Explain why the levels of the liquid are at different heights.[3]
b. The density of the liquid in the tube is $8.7 \times 10^2 \mathrm{~kg} \mathrm{~m}^{-3}$ and the density of air is $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$. The difference in the level of the liquid is $6.0 \mathrm{~cm}$.[3]
Determine the speed of air at A.
▶️Answer/Explanation
Ans:
a. air speed at $\mathrm{A}$ greater than at $\mathrm{B} /$ speed at $\mathrm{B}$ is zero
OR
total/stagnation pressure $« P_{\mathrm{B}} »-$ static pressure $« P_{\mathrm{A}} »=$ dynamic pressure
so $P_{\mathrm{A}}$ is less than at $P_{\mathrm{B}}$ (or vice versa) «by Bernoulli effect»
height of the liquid column is related to «dynamic» pressure difference «hence lower height in arm $B » \checkmark$
b. $« \rho_{\text {liquid }} \mathrm{gh}=0.5 \times \rho_{\text {air }} \mathrm{v}^2 »$
difference in pressure $\mathrm{P}_{\mathrm{B}}-\mathrm{P}_{\mathrm{A}}=8.7 \times 10^2 \times 9.8 \times 0.06=510$ «Pa»
correct substitution into the Bernoulli equation, eg: $\frac{1}{2} \times 1.2 \mathrm{v}^2=510$
$\mathrm{v}=29 \ll \mathrm{ms}^{-1} »$
Question
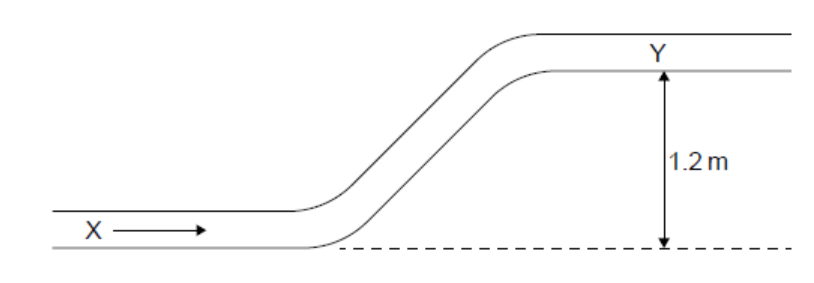
Gasoline of density $720 \mathrm{~kg} \mathrm{~m}^{-3}$ flows in a pipe of constant diameter.
a. State one condition that must be satisfied for the Bernoulli equation[1]
$
\frac{1}{2} \rho v^2+\rho g z+\rho=\text { constant }
$
to apply
b.i. Outline why the speed of the gasoline at $\mathrm{X}$ is the same as that at $\mathrm{Y}$.[1]
b.ii.Calculate the difference in pressure between $\mathrm{X}$ and $\mathrm{Y}$.[2]
b.iiiThe diameter at $\mathrm{Y}$ is made smaller than that at $\mathrm{X}$. Explain why the pressure difference between $\mathrm{X}$ and $\mathrm{Y}$ will increase.[2]
▶️Answer/Explanation
Ans:
a. flow must be laminar/steady/not turbulent
fluid must be incompressible/have constant density
fluid must be non viscous
b.i. «continuity equation says» $A v=$ constant «and the areas are the same»
b.ii.Bernoulli: « $\frac{1}{2} \rho v_{\mathrm{x}}^2+0+P_x=\frac{1}{2} \rho v_{\mathrm{y}}^2+p g H+P_y$ » gives $P_x-P_y=p g H \smile$
$P_{\mathrm{x}}-P_{\mathrm{y}}=720 \times 9.81 \times 1.2=8.5$ «kPa»
Award [2] for bald correct answer.
Watch for POT mistakes.
b.iii the fluid speed at $\mathrm{Y}$ will be greater «than that at $\mathrm{X}$ »
reducing the pressure at $Y$
OR
the formula used to show that the difference is increased