Question
A flywheel is made of a solid disk with a mass $M$ of $5.00 \mathrm{~kg}$ mounted on a small radial axle. The mass of the axle is negligible. The radius $R$ of the disk is $6.00 \mathrm{~cm}$ and the radius $r$ of the axle is $1.20 \mathrm{~cm}$.
A string of negligible thickness is wound around the axle. The string is pulled by an electric motor that exerts a vertical tension force $T$ on the flywheel. The diagram shows the forces acting on the flywheel. $W$ is the weight and $N$ is the normal reaction force from the support of the flywheel.
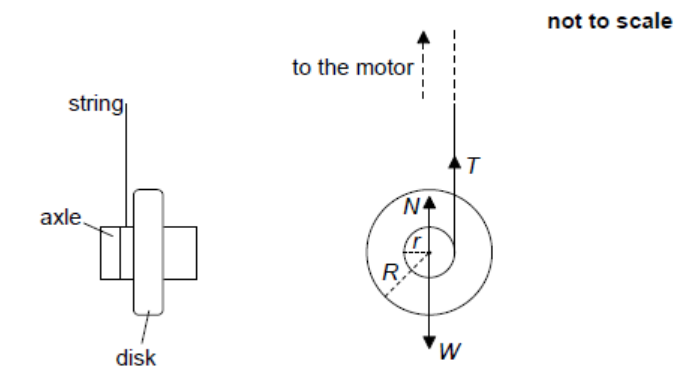
The moment of inertia of the flywheel about the axis is $I=\frac{1}{2} M R^2$.
The flywheel is initially at rest. At time $t=0$ the motor is switched on and a time-varying tension force acts on the flywheel. The torque $\Gamma$ exerted on the flywheel by the tension force in the string varies with $t$ as shown on the graph.
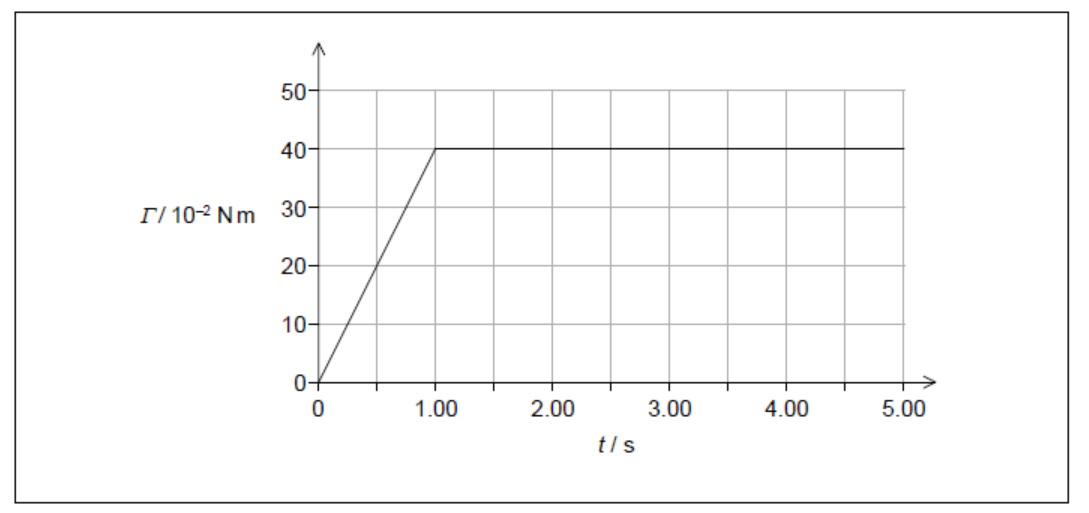
At $t=5.00 \mathrm{~s}$ the string becomes fully unwound and it disconnects from the flywheel. The flywheel remains spinning around the axle.
a. State the torque provided by the force $W$ about the axis of the flywheel.[1]
b(i)Identify the physical quantity represented by the area under the graph.[1]
$\mathrm{b}$ (ii)Show that the angular velocity of the flywheel at $t=5.00 \mathrm{~s}$ is $200 \mathrm{rad} \mathrm{s}^{-1}$.[2]
$\mathrm{b}(\mathrm{iif}$ falculate the maximum tension in the string.
c(i).The flywheel is in translational equilibrium. Distinguish between translational equilibrium and rotational equilibrium.
c(ii)At $t=5.00 \mathrm{~s}$ the flywheel is spinning with angular velocity $200 \mathrm{rad} \mathrm{s}^{-1}$. The support bearings exert a constant frictional torque on the axle. The [3]
flywheel comes to rest after $8.00 \times 10^3$ revolutions. Calculate the magnitude of the frictional torque exerted on the flywheel.
▶️Answer/Explanation
Ans:
a. zero
b(i)«change in» angular momentum
NOTE: Allow angular impulse.
b(ii) «e of $L=I \omega=$ area under graph $=1.80 « \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1} »$
rearranges «to give $\omega=$ area/l» $1.80=0.5 \times 5.00 \times 0.060^2 \times \omega$
«to get $\omega=200 \mathrm{rad} \mathrm{s}^{-1}$ »
$\mathrm{b}(\mathrm{iiik}) \frac{0.40}{0.012}=» 33.3 \mathrm{~N}$
c(i)translational equilibrium is when the sum of all the forces on a body is zero
rotational equilibrium is when the sum of all the torques on a body is zero
c(ii)ALTERNATIVE 1
$
\begin{aligned}
& 0=200^2+2 \times \alpha \times 2 \pi \times 8000 \\
& \alpha=«-» 0.398 \ll \operatorname{rad~s}^{-2} » \\
& \text { torque }=\alpha I=0.398 \times\left(0.5 \times 5.00 \times 0.060^2\right)=3.58 \times 10^{-3}\langle\mathrm{~N} \mathrm{~m} » \\
&
\end{aligned}
$
ALTERNATIVE 2
change in kinetic energy $=\left\langle-\gg 0.5 \times\left(0.5 \times 5.00 \times 0.060^2\right) \times 200^2=\langle-» 180\langle\mathrm{~J} »\right.$
identifies work done $=$ change in $\mathrm{KE}$
torque $=\frac{W}{\theta}=\frac{180}{2 \pi \times 8000}=3.58 \times 10^{-3}\langle\langle\mathrm{~N} \mathrm{~m}\rangle$
Question
A uniform ladder of weight 50.0 N and length 4.00 m is placed against a frictionless wall making an angle of 60.0° with the ground.
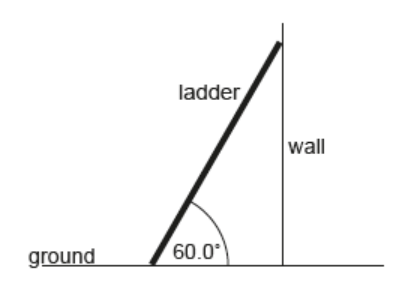
a. Outline why the normal force acting on the ladder at the point of contact with the wall is equal to the frictional force $F$ between the ladder and the
ground.[1]
b. Calculate $F$.[2]
c. The coefficient of friction between the ladder and the ground is 0.400 . Determine whether the ladder will slip.[2]
▶️Answer/Explanation
Ans:
a. «translational equilibrium demands that the» resultant force in the horizontal direction must be zeror
«hence $N_{\mathrm{W}}=F_»$
Equality of forces is given, look for reason why.
b. «clockwise moments = anticlockwise moments»
$
\begin{aligned}
& 50 \times 2 \cos 60=N_{\mathrm{W}} \times 4 \sin 60 \checkmark \\
& « \mathrm{~N}_{\mathrm{W}}=\mathrm{F}=\frac{50 \times 2 \cos 60}{4 \sin 60} » \\
& F=14.4 « N »
\end{aligned}
$
c. maximum friction force $=« 0.4 \times 50 \mathrm{~N} »=20 \ll \mathrm{N} »$
$14.4<20$ AND so will not slip