Question
Evidence from the Planck space observatory suggests that the density of matter in the universe is about $32 \%$ of the critical density of the universe.
a(i)Outline how the light spectra of distant galaxies are used to confirm hypotheses about the expansion of the universe.[2]
a(ii)ight from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength $122 \mathrm{~nm}$. Light from the same spectral line reaching[2]
Earth from a distant galaxy has a wavelength of $392 \mathrm{~nm}$. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
b(i) State what is meant by the critical density.[1]
b(ii)Calculate the density of matter in the universe, using the Hubble constant $70 \mathrm{~km} \mathrm{~s}^{-1} \mathrm{Mpc}^{-1}$.
b(iiil). is estimated that less than $20 \%$ of the matter in the universe is observable. Discuss how scientists use galactic rotation curves to explain this.[2]
▶️Answer/Explanation
Ans:
a(i)spectra of galaxies are redshifted «compared to spectra on Earth»
redshift/longer wavelength implies galaxies recede/ move away from us
OR
redshift is interpreted as cosmological expansion of space
«hence universe expands»
NOTE: Universe expansion is given, so no mark for repeating this.
Do not accept answers based on CMB radiation.
a(ii)ALTERNATIVE 1
$
\begin{aligned}
& z=\frac{392-122}{122}=2.21 \\
& \frac{R}{R_0}=\ll 2.21+1=» 3.21
\end{aligned}
$
ALTERNATIVE 2
$
\begin{aligned}
& \frac{R}{R_0}=\frac{392}{122} \\
& =3.21
\end{aligned}
$
b(i)density of flat/Euclidean universe
OR
density for which universe has zero curvature
OR
density resulting in universe expansion rate tending to zero
$
\begin{aligned}
\mathrm{b}(\text { ii) } \boldsymbol{H} & =\left\langle\frac{70 \times 10^3}{\left(10^6 \times 3.26 \times 9.46 \times 10^{15}\right)}=» 2.27 \times 10^{-18}\left\langle\mathrm{~s}^{-1} » \boldsymbol{V}\right.\right. \\
\rho & =0.32 \times \frac{3 \times\left(2.27 \times 10^{-18}\right)^2}{8 \pi \times 6.67 \times 10^{-11}}
\end{aligned}
$
$3.0 \times 10^{-27}\left\langle\mathrm{~kg} \mathrm{~m}^{-3} » \mathscr{V}\right.$
NOTE: MP1 for conversion of $\mathrm{H}$ to base units.
Allow ECF from MP1, but NOT if $\mathrm{H}$ is left as 70.
$\mathrm{b}$ (iii)otation speed of galaxies is larger than expected away from the centre
there must be more mass «at the edges» than is visually observable «indicating the presence of dark matter»
Question
The homogeneous model of the universe predicts that it may be considered as a spherical cloud of matter of radius r and uniform density ρ. Consider a particle of mass m at the edge of the universe moving with velocity v and obeying Hubble’s law.
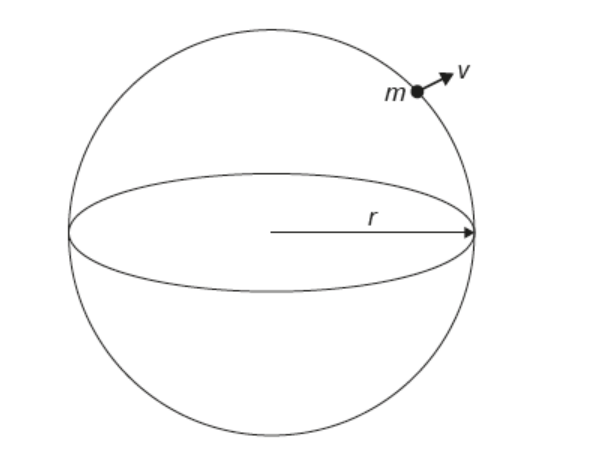
a. Justify that the total energy of this particle is $\mathrm{E}=\frac{1}{2} \mathrm{mv}^2-\frac{4}{3} \pi \mathrm{Grr}^2 \mathrm{~m}$.[2]
b. At critical density there is zero total energy. Show that the critical density of the universe is: $\mathrm{r}_{\mathrm{c}}=\frac{3 \mathrm{H}_0^2}{8 \pi \mathrm{G}}$.[2]
c. The accepted value for the Hubble constant is $2.3 \times 10^{-18} \mathrm{~s}^{-1}$. Estimate the critical density of the universe.[1]
▶️Answer/Explanation
Ans:
a. total energy=kinetic energy+potential energy
OR
total energy $=\frac{1}{2} \mathrm{mv}^2-\frac{\mathrm{GMm}}{\mathrm{r}}$
substitution of $M=\frac{4}{3} \pi \mathrm{r}^3 \rho$
«Hence answer given»
Answer given so for MP2 look for clear evidence that $M_{\text {Universe }}\left(\frac{4}{3} \pi r^3 \rho\right)$ is stated and substituted.
b. substitutes $H_0 r$ for $v \checkmark$
«total energy $=0$ »
$\frac{1}{2} \mathrm{mH}_0^2 \mathrm{r}^2=\frac{4}{3} \pi \mathrm{G}^2 \mathrm{~m}$
«hence $\rho_C=\frac{3 \mathrm{H}_0^2}{8 \pi \mathrm{G}}$ »
Answer given, check working carefully.
c. $9.5 \times 10^{-27}$ « $\mathrm{kgm}^{-3}$ »