IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 4.3 Wave characteristics
Topic 4 Weightage : 5 %
All Questions for Topic 4.3 – Wavefronts and rays , Amplitude and intensity , Superposition , Polarization
Question
Two loudspeakers, A and B, are driven in phase and with the same amplitude at a frequency of 850 Hz. Point P is located 22.5 m from A and 24.3 m from B. The speed of sound is 340 m s–1.
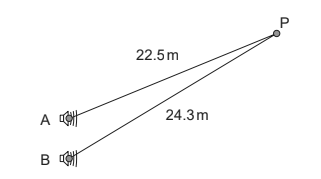
(a) Deduce that a minimum intensity of sound is heard at P. [4]
(b) A microphone moves along the line from P to Q. PQ is normal to the line midway between the loudspeakers.
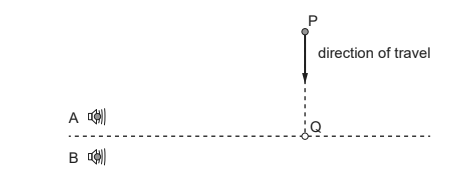
The intensity of sound is detected by the microphone. Predict the variation of detected intensity as the microphone moves from P to Q. [2]
(c) When both loudspeakers are operating, the intensity of sound recorded at Q is I0. Loudspeaker B is now disconnected. Loudspeaker A continues to emit sound with unchanged amplitude and frequency. The intensity of sound recorded at Q changes to IA.
Estimate [2]
(d) In another experiment, loudspeaker A is stationary and emits sound with a frequency of 850 Hz. The microphone is moving directly away from the loudspeaker with a constant speed v. The frequency of sound recorded by the microphone is 845 Hz.
(i) Explain why the frequency recorded by the microphone is lower than the frequency emitted by the loudspeaker. [2]
(ii) Calculate v. [2]
▶️Answer/Explanation
Ans:
a
wavelength = \(\frac{340}{850}\) = 0.40 «m»
path difference = 1.8 «m» 1.8 «m» = 4.5 λ OR \(\frac{1.8}{0.20}\) =9 «half-wavelengths»
waves meet in antiphase «at P»
OR destructive interference/superposition «at P»
b
«equally spaced» maxima and minima
a maximum at Q
four «additional» maxima «between P and Q»
c
the amplitude of sound at Q is halved
«intensity is proportional to amplitude squared hence» \(\frac{I_A}{I_O}=\frac{1}{4}\)
d i
speed of sound relative to the microphone is less
wavelength unchanged «so frequency is lower»
OR
fewer waves recorded in unit time/per second «so frequency is lower»
d ii
845 = 850 × \(\frac{340-V}{340}\)
v = 2.00 «m s-1»
