IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 4.5 Standing waves
Topic 4 Weightage : 5 %
All Questions for Topic 4.5 – The nature of standing waves , Boundary conditions , Nodes and antinodes
Question
One end of a string is attached to an oscillator and the other is fixed to a wall. When the frequency of the oscillator is 360 Hz the standing wave shown is formed on the string.
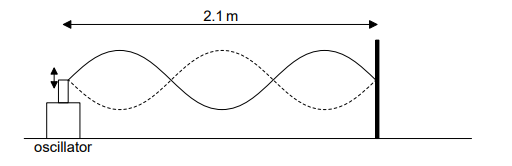
Point X (not shown) is a point on the string at a distance of 10 cm from the oscillator.
(i) State the number of all other points on the string that have the same amplitude and phase as X. [1]
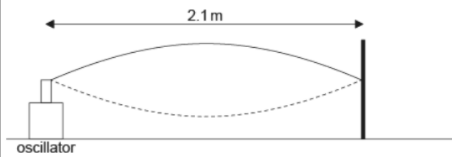
(ii )The frequency of the oscillator is reduced to 120 Hz. On the diagram, draw the standing wave that will be formed on the string. [1]
▶️Answer/Explanation
Ans
i 3 «points»
ii first harmonic mode drawn
Question
On a guitar, the strings played vibrate between two fixed points. The frequency of vibration is modified by changing the string length using a finger. The different strings have different wave speeds. When a string is plucked, a standing wave forms between the bridge and the finger.
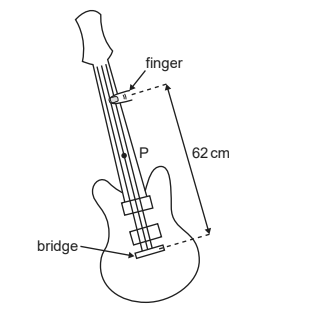
(a) Outline how a standing wave is produced on the string. [2]
(b) The string is displaced 0.4 cm at point P to sound the guitar. Point P on the string vibrates with simple harmonic motion (shm) in its first harmonic with a frequency of 195 Hz. The sounding length of the string is 62 cm.
(i) Show that the speed of the wave on the string is about 240 m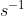 
. [2]
(ii) Sketch a graph to show how the acceleration of point P varies with its displacement from the rest position. [1]
(iii) Calculate, in m 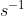, the maximum velocity of vibration of point P when it is vibrating with a frequency of 195 Hz. [2]
(iv) Calculate, in terms of g, the maximum acceleration of P. [2]
(v) Estimate the displacement needed to double the energy of the string. [2]
(c) The string is made to vibrate in its third harmonic. State the distance between consecutive nodes. [1]
▶️Answer/Explanation
Ans:
a «travelling» wave moves along the length of the string and reflects «at fixed end» superposition/interference of incident and reflected waves the superposition of the reflections is reinforced only for certain wavelengths
b i λ = 2 l = 2 × 0.62 = «1.24 m» v = f λ = 195 ×1.24 = 242 «m s-1» Answer must be to 3 or more sf or working shown for MP2
b ii straight line through origin with negative gradient
b iii max velocity occurs at x 0 = V= «(2π)(195) \(\sqrt{0.004^{2}}\) » = 4.9«ms-1 »
b iv a = (2π 195)2 × 0.004 = 6005 «m s−2 » = 600g v use of E =A 2 RO Xo2 A = 0.4 = 0.57 «cm» ≅ 0.6 «cm»
c \(\frac{62}{3}\) = 21«cm»
Related Links