Question
Solve the equations
(a) \(2^{2x}=8^{1-x}\)
(b) \(4^{2x}=8^{1-x}\)
(c) \(2^{x^2+3}=16^x\)
Answer/Explanation
Ans
(a) x = 3/5 (b) x = 3/7 (c) x = 1 or x = 3
Question
Solve the equations
(a) \(25^{x+1}=\frac{1}{5^x}\) (b) \(25^{x+1}=\sqrt{5^x}\)
(c) \(25^{x^2}=125^x\) (d) \(7^{x^2-5x} = 1\)
Answer/Explanation
Ans
(a) x = -2/3 (b) x = -4/3 (c) x = 0 or x = 3/2 (d) x = 0 or x = 5
Question
Sketch the graph of the function \(f(x)=2^x+2\). Indicate the y-intercept, the horizontal asymptote and points A(1,a), B(2,b) and C(3,c) of the graph.
Answer/Explanation
Ans
y-intercept: (0,3), horizontal asymptote: y = 2
Graph for 3 and 4 are shown below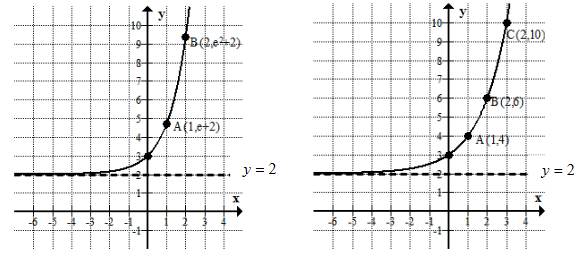
Question
Each year for the past five years the population of a certain country has increased at a steady rate of 2.7% per annum. The present population is 15.2 million.
(a) What was the population one year ago?
(b) What was the population five years ago?
Answer/Explanation
Ans
(a) \(\frac{15.2}{1.027}=14.8\) million
(b) \(\frac{15.2}{(1.027)^5}=13.3\) million (OR 15.2(1.027)-5)
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.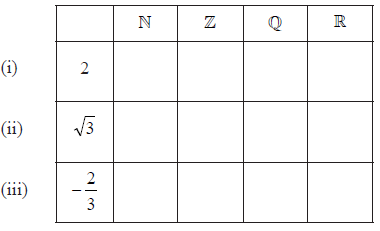
A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).
Answer/Explanation
Markscheme
 (A1)(A1)(A1) (C3)
(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.
[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.
[1 mark]
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.
A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).
Answer/Explanation
Markscheme
 (A1)(A1)(A1) (C3)
(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.
[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.
[1 mark]