Question
Maya planted four sunflowers in order of height, from shortest to tallest.
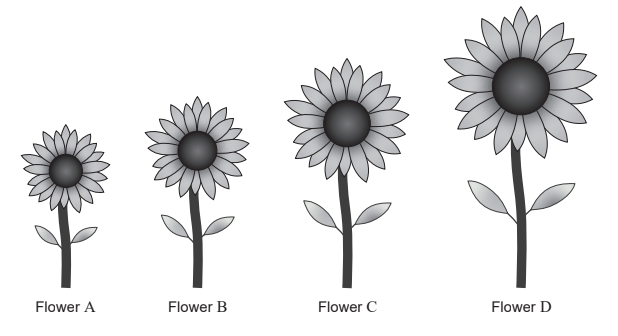
Flower C is 32 cm tall.
The median height of the flowers is 24 cm.
Find the height of Flower B. [2]
The range of the heights is 50 cm. The height of Flower A is p cm and the height of Flower D is q cm.
Using this information, write down an equation in p and q . [1]
The mean height of the flowers is 27 cm.
Write down a second equation in p and q . [1]
Using your answers to parts (b) and (c), find the height of
Flower A;
Flower D. [2]
Answer/Explanation
Ans:
(a)
24-8
OR
24-(32-24)
OR
24 = \(\frac{32+h}{2}\)
16(cm)
(b) q-p= 50 (or equivalent)
(c)\(\frac{p+16+32+q}{4}\)= 27
(d)
(i) 5 (cm)
(ii) 55 (cm)
Question
A box contains 100 cards. Each card has a number between one and six written on it. The following table shows the frequencies for each number.

Calculate the value of k.
Find
(i) the median;
(ii) the interquartile range.
Answer/Explanation
Markscheme
evidence of using \(\sum {{f_i} = 100} \) (M1)
\(k = 4\) A1 N2
[2 marks]
(i) evidence of median position (M1)
e.g. 50th item, \(26 + 10 + 20 = 56\)
\({\text{median}} = 3\) A1 N2
(ii) \({Q_1} = 1\) and \({Q_3} = 5\) (A1)(A1)
\({\text{interquartile range}} = 4\) (accept 1 to 5 or \(5 – 1\) , etc.) A1 N3
[5 marks]
Question
The cumulative frequency curve below represents the marks obtained by 100 students.
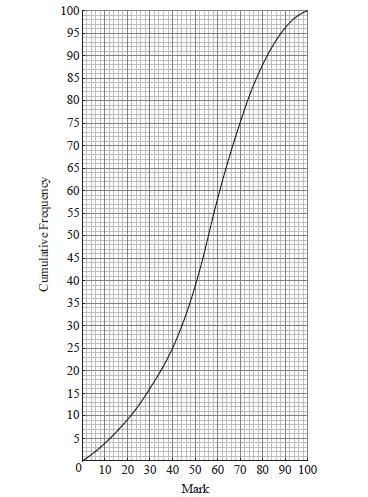
Find the median mark.
Find the interquartile range.
Answer/Explanation
Markscheme
evidence of median position (M1)
e.g. 50, line on sketch
median is 56 A1 N2
[2 marks]
lower quartile \(= 40\) , upper quartile \(= 70\) (A1)(A1)
interquartile range \(= 30\) A1 N3
[3 marks]