Question
Italia’s Pizza Company supplies and delivers large cheese pizzas.
The total cost to the customer, C, in GBP, is modelled by the function
C (n) = 34.50 n + 8.50 , n ≥ 2 , n ∈ Z ,
where n , is the number of large cheese pizzas ordered. This total cost includes a fixed
cost for delivery.
State, in the context of the question,
what the value of 34.50 represents;
what the value of 8.50 represents. [2]
Write down the minimum number of pizzas that can be ordered. [1] Aayush has 450 GBP.
Find the maximum number of large cheese pizzas that Aayush can order from Italia’s Pizza Company. [3]
Answer/Explanation
Ans:
(a)
(i) the cost of each (large cheese) pizza / a pizza / one pizza / per pizza
(ii) the (fixed) delivery cost
(b) 2
(c) 450=34.50n+8.50 12.8 (12.7971…)12
Question
Part of the graph of a function f is shown in the diagram below.
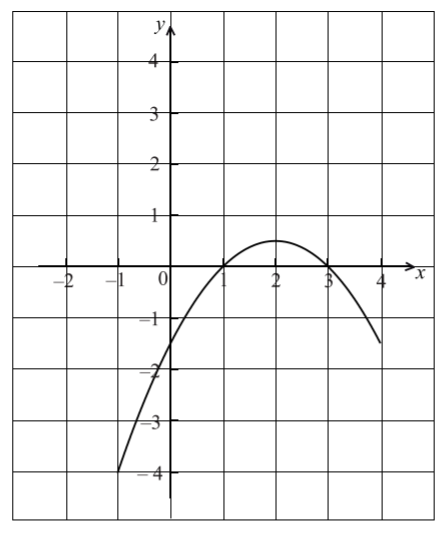
On the same diagram sketch the graph of \(y = – f(x)\) .[2]
Let \(g(x) = f(x + 3)\) .
(i) Find \(g( – 3)\) .
(ii) Describe fully the transformation that maps the graph of f to the graph of g.[4]
Answer/Explanation
Markscheme
 M1A1 N2
M1A1 N2
Note: Award M1 for evidence of reflection in x-axis, A1 for correct vertex and all intercepts approximately correct.
(i) \(g( – 3) = f(0)\) (A1)
\(f(0) = – 1.5\) A1 N2
(ii) translation (accept shift, slide, etc.) of \(\left( {\begin{array}{*{20}{c}}
{ – 3}\\
0
\end{array}} \right)\) A1A1 N2
[4 marks]
Question
Let f be the function given by \(f(x) = {{\rm{e}}^{0.5x}}\) , \(0 \le x \le 3.5\) . The diagram shows the graph of f .
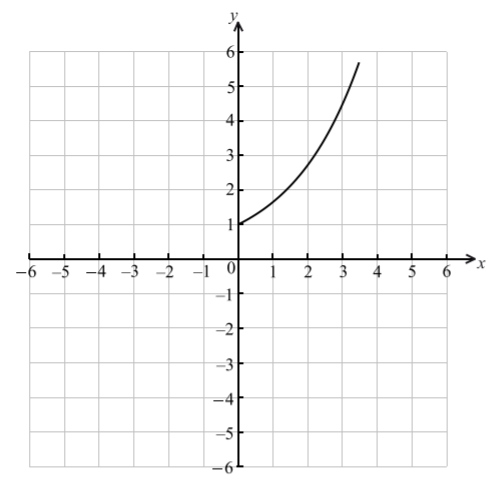
 On the same diagram, sketch the graph of \({f^{ – 1}}\) .[3]
On the same diagram, sketch the graph of \({f^{ – 1}}\) .[3]
Write down the range of \({f^{ – 1}}\) .[1]
Find \({f^{ – 1}}(x)\) .[3]
Answer/Explanation
Markscheme

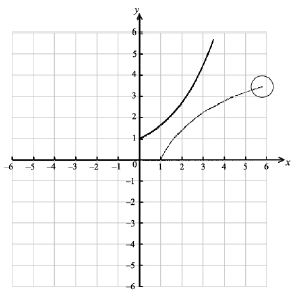
A1A1A1 N3
Note: Award A1 for approximately correct (reflected) shape, A1 for right end point in circle, A1 for through \((1{\text{, }}0)\) .
\(0 \le y \le 3.5\) A1 N1
[1 mark]
interchanging x and y (seen anywhere) M1
e.g. \(x = {e^{0.5y}}\)
evidence of changing to log form A1
e.g. \(\ln x = 0.5y\) , \(\ln x = \ln {{\rm{e}}^{0.5y}}\) (any base), \(\ln x = 0.5y\ln {\rm{e}}\) (any base)
\({f^{ – 1}}(x) = 2\ln x\) A1 N1
[3 marks]
Question
Consider the functions \(f(x)\) , \(g(x)\) and \(h(x)\) . The following table gives some values associated with these functions.
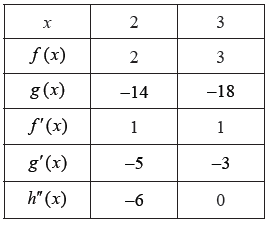

The following diagram shows parts of the graphs of \(h\) and \(h”\) .
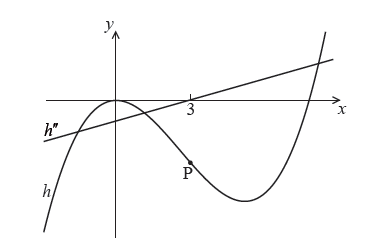

There is a point of inflexion on the graph of \(h\) at P, when \(x = 3\) .
Given that \(h(x) = f(x) \times g(x)\) ,
Write down the value of \(g(3)\) , of \(f'(3)\) , and of \(h”(2)\) .[3]
Explain why P is a point of inflexion.[2]
find the \(y\)-coordinate of P.[2]
find the equation of the normal to the graph of \(h\) at P.[7]
Answer/Explanation
Markscheme
\(g(3) = – 18\) , \(f'(3) = 1\) , \(h”(2) = – 6\) A1A1A1 N3
[3 marks]
\(h”(3) = 0\) (A1)
valid reasoning R1
eg \({h”}\) changes sign at \(x = 3\) , change in concavity of \(h\) at \(x = 3\)
so P is a point of inflexion AG N0
[2 marks]
writing \(h(3)\) as a product of \(f(3)\) and \(g(3)\) A1
eg \(f(3) \times g(3)\) , \(3 \times ( – 18)\)
\(h(3) = – 54\) A1 N1
[2 marks]
recognizing need to find derivative of \(h\) (R1)
eg \({h’}\) , \(h'(3)\)
attempt to use the product rule (do not accept \(h’ = f’ \times g’\) ) (M1)
eg \(h’ = fg’ + gf’\) , \(h'(3) = f(3) \times g'(3) + g(3) \times f'(3)\)
correct substitution (A1)
eg \(h'(3) = 3( – 3) + ( – 18) \times 1\)
\(h'(3) = – 27\) A1
attempt to find the gradient of the normal (M1)
eg \( – \frac{1}{m}\) , \( – \frac{1}{{27}}x\)
attempt to substitute their coordinates and their normal gradient into the equation of a line (M1)
eg \( – 54 = \frac{1}{{27}}(3) + b\) , \(0 = \frac{1}{{27}}(3) + b\) , \(y + 54 = 27(x – 3)\) , \(y – 54 = \frac{1}{{27}}(x + 3)\)
correct equation in any form A1 N4
eg \(y + 54 = \frac{1}{{27}}(x – 3)\) , \(y = \frac{1}{{27}}x – 54\frac{1}{9}\)
[7 marks]
Question
[Maximum mark: 6] [without GDC]
Find the largest possible domain for the following functions
\(f(x)=3-6x\) \(g(x)=\frac{7}{3-6x}\) \(h(x)=\sqrt{3-6x}\) \(k(x)= log(3-6x)\)
Answer/Explanation
Df: x ∈ R , Dg: x ≠ 1/ 2 , Dh: x ≤ 1/ 2 , Dk: x < 1/ 2 ,