Question
The function f is defined by f(x) = \(\frac{7x + 7}{2x – 4}\) for \(x\epsilon \mathbb{R}\), x ≠ 2.
(a) Find the zero of f(x).
(b) For the graph of y = f(x), write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.
(c) Find \(f^{-1}\) (x), the inverse function of f(x).
Answer/Explanation
Answer:
(a) recognizing f(x) = 0
x = -1
(b) (i) x = 2 (must be an equation with x)
(ii) y = \(\frac{7}{2}\) (must be an equation with y)
(c) EITHER
interchanging x and y
2xy – 4x = 7y + 7
correct working with y terms on the same side: 2xy – 7y = 4x + 7
OR
2yx – 4y = 7x +7
correct working with x terms on the same side: 2yx – 7x = 4x + 7
interchanging x and y OR making x the subject x = \(\frac{4y + 7}{2y – 7}\)
THEN
\(f^{-1}\)(x) = \(\frac{4x + 7}{2x – 7}\) (or equivalent) (\(x ≠ \frac{7}{2}\))
Question
The diagram below shows the graph of a function \(f\) , for \( – 1 \le x \le 2\) .
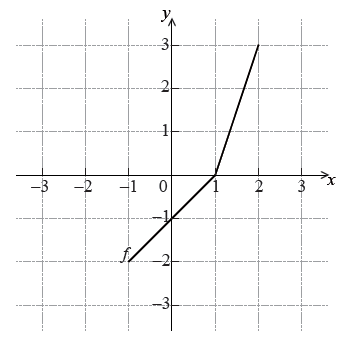
Write down the value of \(f(2)\).[1]
Write down the value of \({f^{ – 1}}( – 1)\) .[2]
Sketch the graph of \({f^{ – 1}}\) on the grid below.
[3]
Answer/Explanation
Markscheme
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ – 1}}( – 1) = 0\) A2 N2
[2 marks]
EITHER
attempt to draw \(y = x\) on grid (M1)
OR
attempt to reverse x and y coordinates (M1)
eg writing or plotting at least two of the points
\(( – 2, – 1)\) , \(( – 1,0)\) , \((0,1)\) , \((3,2)\)
THEN
correct graph A2 N3
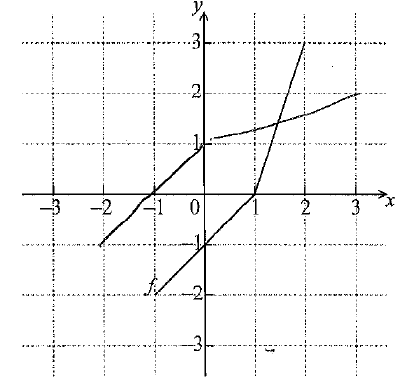
[3 marks]
Question
The following diagram shows the graph of \(y = f(x)\), for \( – 4 \le x \le 5\).
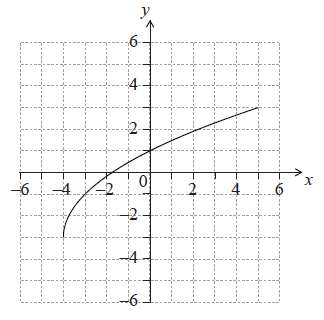
Write down the value of \(f( – 3)\).[1]
Write down the value of \({f^{ – 1}}(1)\).[1]
Find the domain of \({f^{ – 1}}\).[2]
On the grid above, sketch the graph of \({f^{ – 1}}\).[3]
Answer/Explanation
Markscheme
\(f( – 3) = – 1\) A1 N1
[1 mark]
\({f^{ – 1}}(1) = 0\) (accept \(y = 0\)) A1 N1
[1 mark]
domain of \({f^{ – 1}}\) is range of \(f\) (R1)
eg \({\text{R}}f = {\text{D}}{f^{ – 1}}\)
correct answer A1 N2
eg \( – 3 \leqslant x \leqslant 3,{\text{ }}x \in [ – 3,{\text{ }}3]{\text{ (accept }} – 3 < x < 3,{\text{ }} – 3 \leqslant y \leqslant 3)\)
[2 marks]
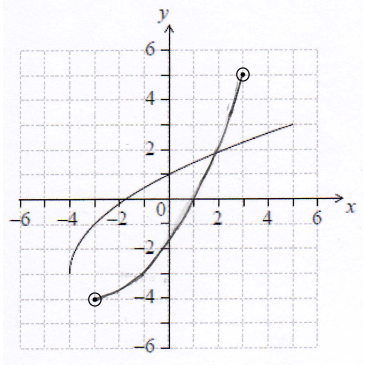A1A1 N2
Note: Graph must be approximately correct reflection in \(y = x\).
Only if the shape is approximately correct, award the following:
A1 for x-intercept at \(1\), and A1 for endpoints within circles.
[2 marks]