Question
Let y = \(\frac{Inx}{x^{4}}\) for x > 0.
(a) Show that \(\frac{dy}{dx}= \frac{1-4Inx}{x^{5}}\)
Consider the function defined by f (x) \(\frac{Inx}{x^{4}}\) = for x> 0 and its graph y = f (x) .
(b) The graph of f has a horizontal tangent at point P. Find the coordinates of P. [5]
(c) Given that f ” (x) = \(\frac{20Lnx-9}{x^{6}}\) show that P is a local maximum point. [3]
(d) Solve f (x) > 0 for x > 0. [2]
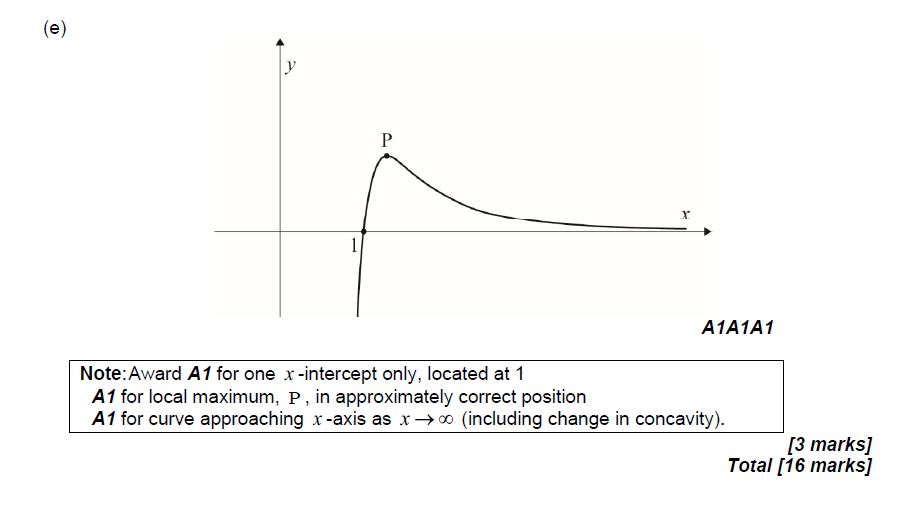
(e) Sketch the graph of f , showing clearly the value of the x-intercept and the approximate position of point P. [3]
Answer/Explanation
Ans



Question
Let \(f(x) = 3 + \frac{{20}}{{{x^2} – 4}}\) , for \(x \ne \pm 2\) . The graph of f is given below.
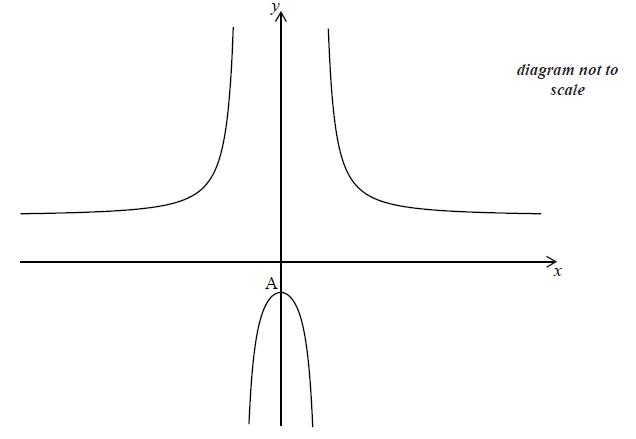
The y-intercept is at the point A.
(i) Find the coordinates of A.
(ii) Show that \(f'(x) = 0\) at A.[7]
The second derivative \(f”(x) = \frac{{40(3{x^2} + 4)}}{{{{({x^2} – 4)}^3}}}\) . Use this to
(i) justify that the graph of f has a local maximum at A;
(ii) explain why the graph of f does not have a point of inflexion.[6]
Describe the behaviour of the graph of \(f\) for large \(|x|\) .[1]
Write down the range of \(f\) .[2]
Answer/Explanation
Markscheme
(i) coordinates of A are \((0{\text{, }} – 2)\) A1A1 N2
(ii) derivative of \({x^2} – 4 = 2x\) (seen anywhere) (A1)
evidence of correct approach (M1)
e.g. quotient rule, chain rule
finding \(f'(x)\) A2
e.g. \(f'(x) = 20 \times ( – 1) \times {({x^2} – 4)^{ – 2}} \times (2x)\) , \(\frac{{({x^2} – 4)(0) – (20)(2x)}}{{{{({x^2} – 4)}^2}}}\)
substituting \(x = 0\) into \(f'(x)\) (do not accept solving \(f'(x) = 0\) ) M1
at A \(f'(x) = 0\) AG N0
[7 marks]
(i) reference to \(f'(x) = 0\) (seen anywhere) (R1)
reference to \(f”(0)\) is negative (seen anywhere) R1
evidence of substituting \(x = 0\) into \(f”(x)\) M1
finding \(f”(0) = \frac{{40 \times 4}}{{{{( – 4)}^3}}}\) \(\left( { = – \frac{5}{2}} \right)\) A1
then the graph must have a local maximum AG
(ii) reference to \(f”(x) = 0\) at point of inflexion (R1)
recognizing that the second derivative is never 0 A1 N2
e.g. \(40(3{x^2} + 4) \ne 0\) , \(3{x^2} + 4 \ne 0\) , \({x^2} \ne – \frac{4}{3}\) , the numerator is always positive
Note: Do not accept the use of the first derivative in part (b).
[6 marks]
correct (informal) statement, including reference to approaching \(y = 3\) A1 N1
e.g. getting closer to the line \(y = 3\) , horizontal asymptote at \(y = 3\)
[1 mark]
correct inequalities, \(y \le – 2\) , \(y > 3\) , FT from (a)(i) and (c) A1A1 N2
[2 marks]
Question
Let \(f(x) = 6 + 6\sin x\) . Part of the graph of f is shown below.
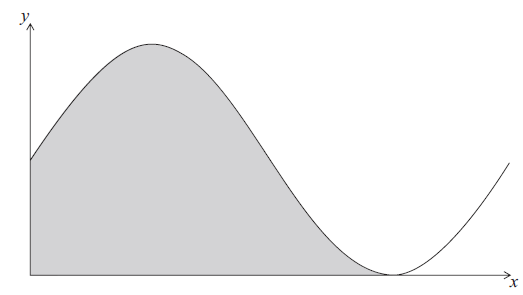
The shaded region is enclosed by the curve of f , the x-axis, and the y-axis.
Solve for \(0 \le x < 2\pi \)
(i) \(6 + 6\sin x = 6\) ;
(ii) \(6 + 6\sin x = 0\) .[5]
Write down the exact value of the x-intercept of f , for \(0 \le x < 2\pi \) .[1]
The area of the shaded region is k . Find the value of k , giving your answer in terms of \(\pi \) .[6]
Let \(g(x) = 6 + 6\sin \left( {x – \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Give a full geometric description of this transformation.[2]
Let \(g(x) = 6 + 6\sin \left( {x – \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Given that \(\int_p^{p + \frac{{3\pi }}{2}} {g(x){\rm{d}}x} = k\) and \(0 \le p < 2\pi \) , write down the two values of p.[3]
Answer/Explanation
Markscheme
(i) \(\sin x = 0\) A1
\(x = 0\) , \(x = \pi \) A1A1 N2
(ii) \(\sin x = – 1\) A1
\(x = \frac{{3\pi }}{2}\) A1 N1
[5 marks]
\(\frac{{3\pi }}{2}\) A1 N1
[1 mark]
evidence of using anti-differentiation (M1)
e.g. \(\int_0^{\frac{{3\pi }}{2}} {(6 + 6\sin x){\rm{d}}x} \)
correct integral \(6x – 6\cos x\) (seen anywhere) A1A1
correct substitution (A1)
e.g. \(6\left( {\frac{{3\pi }}{2}} \right) – 6\cos \left( {\frac{{3\pi }}{2}} \right) – ( – 6\cos 0)\) , \(9\pi – 0 + 6\)
\(k = 9\pi + 6\) A1A1 N3
[6 marks]
translation of \(\left( {\begin{array}{*{20}{c}}
{\frac{\pi }{2}}\\
0
\end{array}} \right)\) A1A1 N2
[2 marks]
recognizing that the area under g is the same as the shaded region in f (M1)
\(p = \frac{\pi }{2}\) , \(p = 0\) A1A1 N3
[3 marks]