Question
Let \(f(x) = 3\sin \left( {\frac{\pi }{2}x} \right)\), for \(0 \leqslant x \leqslant 4\).
(i) Write down the amplitude of \(f\).
(ii) Find the period of \(f\).[3]
On the following grid sketch the graph of \(f\).
[4]
Answer/Explanation
Markscheme
(i) 3 A1 N1
(ii) valid attempt to find the period (M1)
eg\(\,\,\,\,\,\)\(\frac{{2\pi }}{b},{\text{ }}\frac{{2\pi }}{{\frac{\pi }{2}}}\)
period \( = 4\) A1 N2
[3 marks]
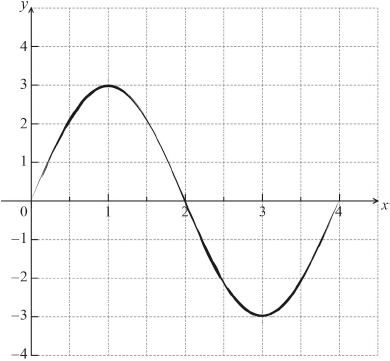A1A1A1A1 N4
[4 marks]
Question
The following diagram shows the graph of a function \(f\), with domain \( – 2 \leqslant x \leqslant 4\).
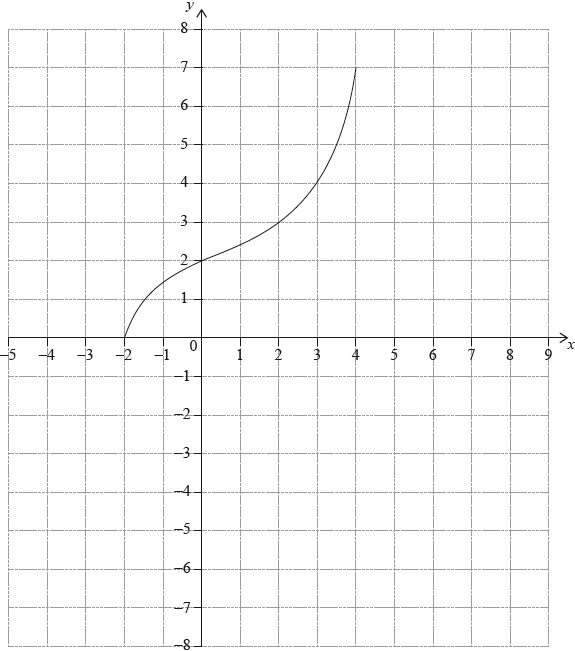
The points \(( – 2,{\text{ }}0)\) and \((4,{\text{ }}7)\) lie on the graph of \(f\).
Write down the range of \(f\).[1]
Write down \(f(2)\);[1]
Write down \({f^{ – 1}}(2)\).[1]
On the grid, sketch the graph of \({f^{ – 1}}\).[3]
Answer/Explanation
Markscheme
correct range (do not accept \(0 \leqslant x \leqslant 7\)) A1 N1
eg\(\,\,\,\,\,\)\([0,{\text{ }}7],{\text{ }}0 \leqslant y \leqslant 7\)
[1 mark]
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ – 1}}(2) = 0\) A1 N1
[1 mark]
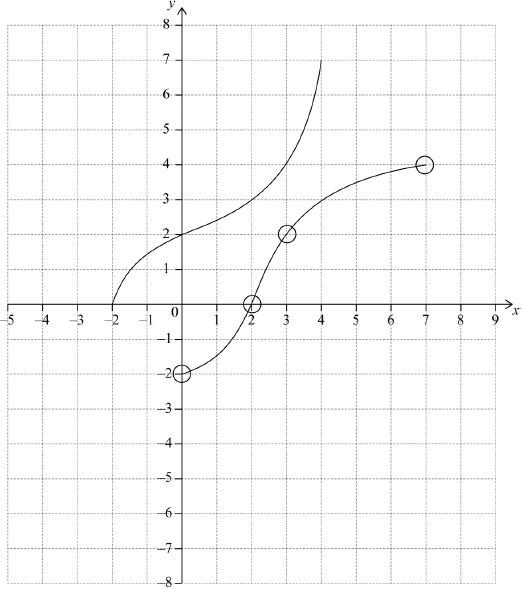A1A1A1 N3
Notes: Award A1 for both end points within circles,
A1 for images of \((2,{\text{ }}3)\) and \((0,{\text{ }}2)\) within circles,
A1 for approximately correct reflection in \(y = x\), concave up then concave down shape (do not accept line segments).
[3 marks]
Question
Consider a function f (x) , for −2 ≤ x ≤ 2 . The following diagram shows the graph of f.
Write down the value of f (0).[1]
Write down the value of f −1 (1).[1]
Write down the range of f −1.[1]
On the grid above, sketch the graph of f −1.[4]
Answer/Explanation
Markscheme
\(f\left( 0 \right) = – \frac{1}{2}\) A1 N1
[1 mark]
f −1 (1) = 2 A1 N1
[1 mark]
−2 ≤ y ≤ 2, y∈ [−2, 2] (accept −2 ≤ x ≤ 2) A1 N1
[1 mark]
A1A1A1A1 N4
Note: Award A1 for evidence of approximately correct reflection in y = x with correct curvature.
(y = x does not need to be explicitly seen)
Only if this mark is awarded, award marks as follows:
A1 for both correct invariant points in circles,
A1 for the three other points in circles,
A1 for correct domain.
[4 marks]