Question
Let \(f\) be a quadratic function. Part of the graph of \(f\) is shown below.
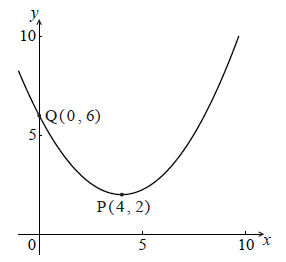
The vertex is at P(\(4\), \(2\)) and the y-intercept is at Q(\(0\), \(6\)) .
Write down the equation of the axis of symmetry.[1]
The function f can be written in the form \(f(x) = a{(x – h)^2} + k\) .
Write down the value of h and of k .[2]
The function f can be written in the form \(f(x) = a{(x – h)^2} + k\) .Find a .
Answer/Explanation
Markscheme
\(x = 4\) (must be an equation) A1 N1
[1 mark]
\(h = 4\) , \(k = 2\) A1A1 N2
[2 marks]
attempt to substitute coordinates of any point on the graph into f (M1)
e.g. \(f(0) = 6\) , \(6 = a{(0 – 4)^2} + 2\) , \(f(4) = 2\)
correct equation (do not accept an equation that results from \(f(4) = 2\) ) (A1)
e.g. \(6 = a{( – 4)^2} + 2\) , \(6 = 16a + 2\)
\(a = \frac{4}{{16}}\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
Question
Let \(f(x) = a{(x – h)^2} + k\). The vertex of the graph of \(f\) is at \((2, 3)\) and the graph passes through \((1, 7)\).
Write down the value of \(h\) and of \(k\).
Find the value of \(a\).
Answer/Explanation
Markscheme
\(h = 2,{\text{ }}k = 3\) A1A1 N2
[2 marks]
attempt to substitute \((1,7)\) in any order into their \(f(x)\) (M1)
eg \(7 = a{(1 – 2)^2} + 3{\text{, }}7 = a{(1 – 3)^2} + 2{\text{, }}1 = a{(7 – 2)^2} + 3\)
correct equation (A1)
eg \(7 = a + 3\)
a = 4 A1 N2
[3 marks]
Question
Let \(f(x) = 3{x^2} – 6x + p\). The equation \(f(x) = 0\) has two equal roots.
Write down the value of the discriminant.[2]
Hence, show that \(p = 3\).[1]
The graph of \(f\)has its vertex on the \(x\)-axis.
Find the coordinates of the vertex of the graph of \(f\).[4]
The graph of \(f\) has its vertex on the \(x\)-axis.
Write down the solution of \(f(x) = 0\).[1]
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(a\).[1]
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(h\).[1]
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(k\).[1]
The graph of \(f\) has its vertex on the \(x\)-axis.
The graph of a function \(g\) is obtained from the graph of \(f\) by a reflection of \(f\) in the \(x\)-axis, followed by a translation by the vector \(\left( \begin{array}{c}0\\6\end{array} \right)\). Find \(g\), giving your answer in the form \(g(x) = A{x^2} + Bx + C\).[4]
Answer/Explanation
Markscheme
correct value \(0\), or \(36 – 12p\) A2 N2
[2 marks]
correct equation which clearly leads to \(p = 3\) A1
eg \(36 – 12p = 0,{\text{ }}36 = 12p\)
\(p = 3\) AG N0
[1 mark]
METHOD 1
valid approach (M1)
eg \(x = – \frac{b}{{2a}}\)
correct working A1
eg \( – \frac{{( – 6)}}{{2(3)}},{\text{ }}x = \frac{6}{6}\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
METHOD 2
valid approach (M1)
eg \(f(x) = 0\), factorisation, completing the square
correct working A1
eg \({x^2} – 2x + 1 = 0,{\text{ }}(3x – 3)(x – 1),{\text{ }}f(x) = 3{(x – 1)^2}\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
METHOD 3
valid approach using derivative (M1)
eg \(f'(x) = 0,{\text{ }}6x – 6\)
correct equation A1
eg \(6x – 6 = 0\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
[4 marks]
\(x = 1\) A1 N1
[1 mark]
\(a = 3\) A1 N1
[1 mark]
\(h = 1\) A1 N1
[1 mark]
\(k = 0\) A1 N1
[1 mark]
attempt to apply vertical reflection (M1)
eg \( – f(x),{\text{ }} – 3{(x – 1)^2}\), sketch
attempt to apply vertical shift 6 units up (M1)
eg \( – f(x) + 6\), vertex \((1, 6)\)
transformations performed correctly (in correct order) (A1)
eg \( – 3{(x – 1)^2} + 6,{\text{ }} – 3{x^2} + 6x – 3 + 6\)
\(g(x) = – 3{x^2} + 6x + 3\) A1 N3
[4 marks]
Question
Let f(x) = ax2 − 4x − c. A horizontal line, L , intersects the graph of f at x = −1 and x = 3.
The equation of the axis of symmetry is x = p. Find p.[2]
Hence, show that a = 2.[2]
The equation of L is y = 5 . Find the value of c.[3]
Answer/Explanation
Markscheme
METHOD 1 (using symmetry to find p)
valid approach (M1)
eg \(\frac{{ – 1 + 3}}{2}\),
p = 1 A1 N2
Note: Award no marks if they work backwards by substituting a = 2 into \( – \frac{b}{{2a}}\) to find p.
Do not accept \(p = \frac{2}{a}\).
METHOD 2 (calculating a first)
(i) & (ii) valid approach to calculate a M1
eg a + 4 − c = a(32) − 4(3) − c, f(−1) = f(3)
correct working A1
eg 8a = 16
a = 2 AG N0
valid approach to find p (M1)
eg \( – \frac{b}{{2a}},\,\,\,\frac{4}{{2\left( 2 \right)}}\)
p = 1 A1 N2
[2 marks]
METHOD 1
valid approach M1
eg \( – \frac{b}{{2a}},\,\,\,\frac{4}{{2a}}\) (might be seen in (i)), f’ (1) = 0
correct equation A1
eg \(\frac{4}{{2a}}\) = 1, 2a(1) − 4 = 0
a = 2 AG N0
METHOD 2 (calculating a first)
(i) & (ii) valid approach to calculate a M1
eg a + 4 − c = a(32) − 4(3) − c, f(−1) = f(3)
correct working A1
eg 8a = 16
a = 2 AG N0
[2 marks]
valid approach (M1)
eg f(−1) = 5, f(3) =5
correct working (A1)
eg 2 + 4 − c = 5, 18 − 12 − c = 5
c = 1 A1 N2
[3 marks]
Question
[Maximum mark: 4] [without GDC]
The diagram shows the graph of the function \(y = ax^{2}+bx+c\).
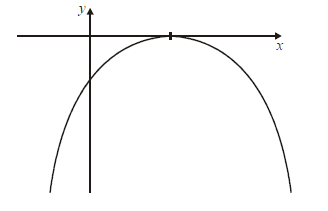
Complete the table below to show whether each expression is positive, negative or
zero.
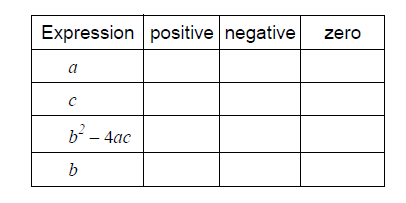
Answer/Explanation
Ans.
Graph of quadratic function.