Question
The diagram shows the graph of the quadratic function \(f(x)=ax^2+bx+c\) , with vertex −2, 10) .
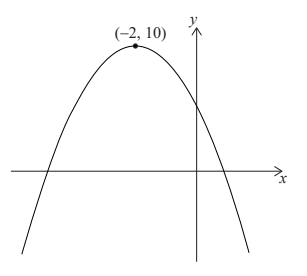
The equation f (x) = k has two solutions. One of these solutions is x = 2 .
Write down the other solution of f (x) = k . [2]
Complete the table below placing a tick (✔) to show whether the unknown parameters
a and b are positive, zero or negative. The row for c has been completed as an example. [2]
positive
zero
negative
a
b
c
✔
State the values of x for which f (x) is decreasing. [2]
Answer/Explanation
Ans:
(a)
(x= (-2))-4 OR x= (-2)- (2-(-2))
X= -6
(b) 
(c) x > −2 OR x ≥ −2
Question
Let f (x)=- x2 + 4x + 5 and g (x) = -f (x) + k .
Find the values of k so that g (x) = 0 has no real roots.
Answer/Explanation
Ans:
Method 1(discriminant)
correct expression for g
eg \(-(-x^{2}+4x+5)+k\) ,\( x^{2}\)-4x-5+k = 0
evidence of discriminant
eg \(b^{2}-4ac,\Delta\)
correct substitution into discriminant of g
eg \((-4)^{2}-4(1)(-5+k)\), \(16-4(k-5)\)
recognizing discriminant is negative
eg \(\Delta <0, (-4)^{2}-4(1)(-5+k)<0, 16-4 (-1)(5)<0\)
correct working (must be correct inequality)
eg -4k<-36, k-5>4,16+20-4k<0 k>9


Question
Let f (x) = mx2 – 2mx , where x ∈ \(\mathbb{R}\) and m ∈ \(\mathbb{R}\) The line y = mx – 9 meets the graph of f
at exactly one point.
(a) Show that m = 4 . [6]
The function f can be expressed in the form f (x) = 4(x – p)(x – q) , where p , q ∈ \(\mathbb{R}\).
(b) Find the value of p and the value of q . [2]
The function f can also be expressed in the form f (x) = 4(x – h)2 + k , where h , k ∈ \(\mathbb{R}\).
(c) Find the value of h and the value of k . [3]
(d) Hence find the values of x where the graph of f is both negative and increasing. [3]
Answer/Explanation
Ans

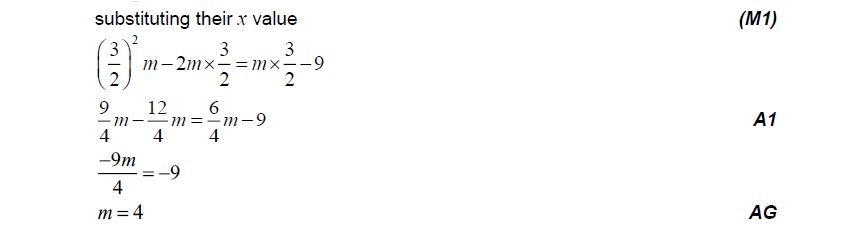
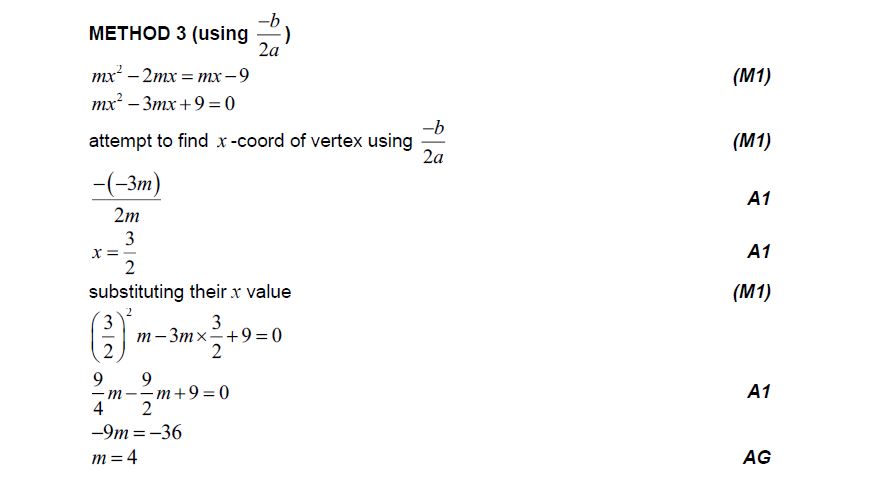

Question
Let \(f(x) = 3{\tan ^4}x + 2k\) and \(g(x) = – {\tan ^4}x + 8k{\tan ^2}x + k\), for \(0 \leqslant x \leqslant 1\), where \(0 < k < 1\). The graphs of \(f\) and \(g\) intersect at exactly one point. Find the value of \(k\).
Answer/Explanation
Markscheme
discriminant \( = 0\) (seen anywhere) M1
valid approach (M1)
eg\(\,\,\,\,\,\)\(f = g,{\text{ }}3{\tan ^4}x + 2k = – {\tan ^4}x + 8k{\tan ^2}x + k\)
rearranging their equation (to equal zero) (M1)
eg\(\,\,\,\,\,\)\(4{\tan ^4}x – 8k{\tan ^2}x + k = 0,{\text{ }}4{\tan ^4}x – 8k{\tan ^2}x + k\)
recognizing LHS is quadratic (M1)
eg\(\,\,\,\,\,\)\(4{({\tan ^2}x)^2} – 8k{\tan ^2}x + k = 0,{\text{ }}4{m^2} – 8km + k\)
correct substitution into discriminant A1
eg\(\,\,\,\,\,\)\({( – 8k)^2} – 4(4)(k)\)
correct working to find discriminant or solve discriminant \( = 0\) (A1)
eg\(\,\,\,\,\,\)\(64{k^2} – 16k,{\text{ }}\frac{{ – ( – 16) \pm \sqrt {{{16}^2}} }}{{2 \times 64}}\)
correct simplification (A1)
egx\(\,\,\,\,\,\)\(16k(4k – 1),{\text{ }}\frac{{32}}{{2 \times 64}}\)
\(k = \frac{1}{4}\) A1 N2
[8 marks]
Question
Three consecutive terms of a geometric sequence are \(x – 3\), 6 and \(x + 2\).
Find the possible values of \(x\).
Answer/Explanation
Markscheme
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}(x – 3) \times r = 6,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(x\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{{x – 3}} = \frac{{x + 2}}{6},{\text{ }}(x – 3)(x + 2) = {6^2},{\text{ }}36 = {x^2} – x – 6\)
correct working (A1)
eg\(\,\,\,\,\,\)\({x^2} – x – 42,{\text{ }}{x^2} – x = 42\)
valid attempt to solve their quadratic equation (M1)
eg\(\,\,\,\,\,\)factorizing, formula, completing the square
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((x – 7)(x + 6),{\text{ }}\frac{{1 \pm \sqrt {169} }}{2}\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
METHOD 2 (finding r first)
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}6r = x + 2,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(r\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{r} + 3 = 6r – 2,{\text{ }}6 + 3r = 6{r^2} – 2r,{\text{ }}6{r^2} – 5r – 6 = 0\)
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((3r + 2)(2r – 3),{\text{ }}\frac{{5 \pm \sqrt {25 + 144} }}{{12}}\)
\(r = – \frac{2}{3},{\text{ }}r = \frac{3}{2}\) A1
substituting their values of \(r\) to find \(x\) (M1)
eg\(\,\,\,\,\,\)\((x – 3)\left( {\frac{2}{3}} \right) = 6,{\text{ }}x = 6\left( {\frac{3}{2}} \right) – 2\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
[6 marks]
Examiners report
Nearly all candidates attempted to set up an expression, or pair of expressions, for the common ratio of the geometric sequence. When done correctly, these expressions led to a quadratic equation which was solved correctly by many candidates.
Question
[Maximum mark: 7] [without GDC]
The quadratic equation \(kx^{2}+(k-3)x+1=0\) has two equal real roots.
(a) Find the possible values of \(k\).
(b) Write down the values of \(k\) for which \(x^{2}+(k-3)x+k=0\) has two equal real roots.
Answer/Explanation
Ans.
(a) \((k-3)^{2}-4xkx1=0, k^{2}-10k+9=0\)
\(k = 1, k = 9\)
(b) \(k = 1, k = 9\)