Question
Find the range of possible values of k such that \(e^{2x}\) + In k = 3\(e^x\) has at least one real solution.
Answer/Explanation
Answer:
recognition of quadratic in \(e^x\)}}\){
\((e^x)^2 – 3e^x + In k(=0)\) OR \(A^2\) – 3A + In k (=0)
recognizing discriminant ≥ 0 (seen anywhere)
\((-3)^2\) – 4(1) (in k) OR 9 – In k
In k ≤ \(\frac{9}{4}\)
\(e^{9/5}\) (seen anywhere)
0 < k ≤ \(e^{9/4}\)
Question
Dominic jumps out of an airplane that is flying at constant altitude. Before opening his
parachute, he goes through a period of freefall.
Dominic’s vertical speed during the time of freefall, S , in m s−1 , is modelled by the following function.
\(S(t)=K-6-(1.2^t),t\geqslant 0\)
where t , is the number of seconds after he jumps out of the airplane, and K is a constant. A sketch
of Dominic’s vertical speed against time is shown below.
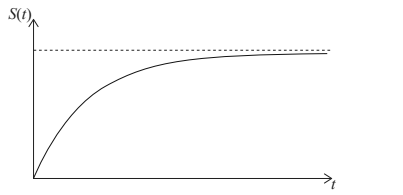
Dominic’s initial vertical speed is \(0\:ms^{-1}\)
Find the value of K . [2]
In the context of the model, state what the horizontal asymptote represents. [1]
Find Dominic’s vertical speed after 10 seconds. Give your answer in km h−1 . [3]
Answer/Explanation
Ans:
(a)
0 = K – 60(1.20)
K= 60
(b)
the (vertical) speed that Dominic is approaching (as t increases)
OR
the limit of the (vertical) speed of Dominic
(c)
S=60-60\((1.2^{-10})\)
\(S=50.3096..(ms^{-1})\)
\(181(kmh^{-1})(181.144..(kmh^{-1}))\)
Question
Let f (x) = a log3 (x – 4) , for x > 4 , where a > 0 .
Point A(13 , 7) lies on the graph of f .
Find the value of a . [3]
The x-intercept of the graph of f is (5 , 0) .
On the following grid, sketch the graph of f . [3]
Answer/Explanation
Ans:
(a)
attempt to substitute coordinates (in any order) into f
eg a \(log_{3} (13-4)=7, alog_{3}\)(7-4)=13 , alog9 = 7
finding \(log_{3}\) 9=2 (seen anywhere)
eg \(log_{3}9=2, 2a=7\)
\(a= \frac{7}{2}\)
(b)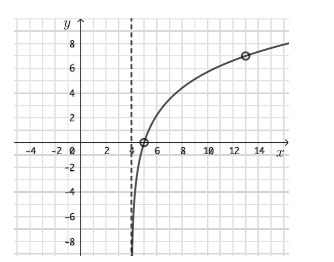 
Question
Let \(f(x) = {\log _p}(x + 3)\) for \(x > – 3\) . Part of the graph of f is shown below.
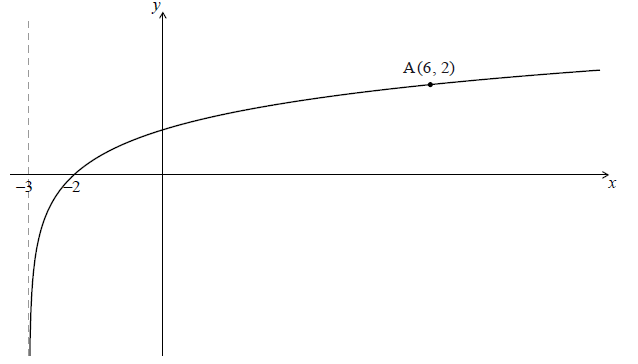
The graph passes through A(6, 2) , has an x-intercept at (−2, 0) and has an asymptote at \(x = – 3\) .
Find p .
The graph of f is reflected in the line \(y = x\) to give the graph of g .
(i) Write down the y-intercept of the graph of g .
(ii) Sketch the graph of g , noting clearly any asymptotes and the image of A.
The graph of \(f\) is reflected in the line \(y = x\) to give the graph of \(g\) .
Find \(g(x)\) .
Answer/Explanation
Markscheme
evidence of substituting the point A (M1)
e.g. \(2 = {\log _p}(6 + 3)\)
manipulating logs A1
e.g. \({p^2} = 9\)
\(p = 3\) A2 N2
[4 marks]
(i) \(y = – 2\) (accept \((0{\text{, }} – 2))\) A1 N1
(ii)
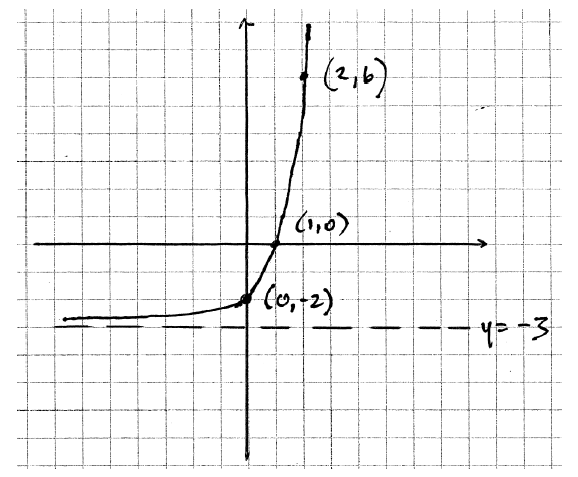A1A1A1A1 N4
Note: Award A1 for asymptote at \(y = – 3\) , A1 for an increasing function that is concave up, A1 for a positive x-intercept and a negative y-intercept, A1 for passing through the point \((2{\text{, }}6)\) .
[5 marks]
METHOD 1
recognizing that \(g = {f^{ – 1}}\) (R1)
evidence of valid approach (M1)
e.g. switching x and y (seen anywhere), solving for x
correct manipulation (A1)
e.g. \({3^x} = y + 3\)
\(g(x) = {3^x} – 3\) A1 N3
METHOD 2
recognizing that \(g(x) = {a^x} + b\) (R1)
identifying vertical translation (A1)
e.g. graph shifted down 3 units, \(f(x) – 3\)
evidence of valid approach (M1)
e.g. substituting point to identify the base
\(g(x) = {3^x} – 3\) A1 N3
[4 marks]