Question
The diagram shows two concentric circles with centre O.
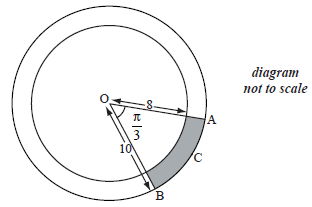
The radius of the smaller circle is 8 cm and the radius of the larger circle is 10 cm.
Points A, B and C are on the circumference of the larger circle such that \({\rm{A}}\widehat {\rm{O}}{\rm{B}}\) is \(\frac{\pi }{3}\) radians.
Find the length of the arc ACB .[2]
Find the area of the shaded region.[4]
Answer/Explanation
Markscheme
correct substitution in \(l = r\theta \) (A1)
e.g. \(10 \times \frac{\pi }{3}\) , \(\frac{1}{6} \times 2\pi \times 10\)
arc length \( = \frac{{20\pi }}{6}\) \(\left( { = \frac{{10\pi }}{3}} \right)\) A1 N2
[2 marks]
area of large sector \( = \frac{1}{2} \times {10^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{100\pi }}{6}} \right)\) (A1)
area of small sector \( = \frac{1}{2} \times {8^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{64\pi }}{6}} \right)\) (A1)
evidence of valid approach (seen anywhere) M1
e.g. subtracting areas of two sectors, \(\frac{1}{2} \times \frac{\pi }{3}({10^2} – {8^2})\)
area shaded \( = 6\pi \) (accept \(\frac{{36\pi }}{6}\) , etc.) A1 N3
[4 marks]
Question
The following diagram shows a circle with centre \(O\) and a radius of \(10\) cm. Points \(A\), \(B\) and \(C\) lie on the circle.
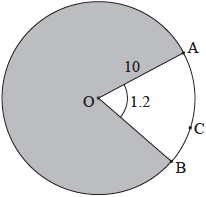
Angle \(AOB\) is \(1.2\) radians.
Find the length of \({\text{arc ACB}}\).[2]
Find the perimeter of the shaded region.[3]
Answer/Explanation
Markscheme
correct substitution (A1)
eg\(\;\;\;10(1.2)\)
\(ACB\) is \(12{\text{ (cm)}}\) A1 N2
[2 marks]
valid approach to find major arc (M1)
eg\(\;\;\;\)circumference \( – {\text{AB}}\), major angle \({\text{AOB}} \times {\text{radius}}\)
correct working for arc length (A1)
eg\(\;\;\;2\pi (10) – 12,{\text{ }}10(2 \times 3.142 – 1.2),{\text{ }}2\pi (10) – 12 + 20\)
perimeter is \(20\pi + 8\;\;\;( = 70.8){\text{ (cm)}}\) A1 N2
[3 marks]
Total [5 marks]
Question
The following diagram shows triangle ABC, with \({\text{AB}} = 3{\text{ cm}}\), \({\text{BC}} = 8{\text{ cm}}\), and \({\rm{A\hat BC = }}\frac{\pi }{3}\).
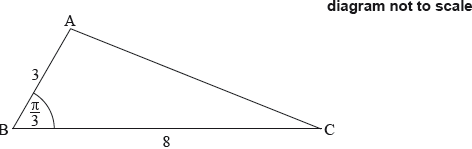
Show that \({\text{AC}} = 7{\text{ cm}}\).[4]
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.
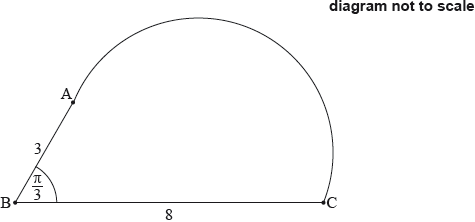
Find the exact perimeter of this shape.[3]
Answer/Explanation
Markscheme
evidence of choosing the cosine rule (M1)
eg\(\,\,\,\,\,\)\({c^2} = {a^2} + {b^2} – ab\cos C\)
correct substitution into RHS of cosine rule (A1)
eg\(\,\,\,\,\,\)\({3^2} + {8^2} – 2 \times 3 \times 8 \times \cos \frac{\pi }{3}\)
evidence of correct value for \(\cos \frac{\pi }{3}\) (may be seen anywhere, including in cosine rule) A1
eg\(\,\,\,\,\,\)\(\cos \frac{\pi }{3} = \frac{1}{2},{\text{ A}}{{\text{C}}^2} = 9 + 64 – \left( {48 \times \frac{1}{2}} \right),{\text{ }}9 + 64 – 24\)
correct working clearly leading to answer A1
eg\(\,\,\,\,\,\)\({\text{A}}{{\text{C}}^2} = 49,{\text{ }}b = \sqrt {49} \)
\({\text{AC}} = 7{\text{ (cm)}}\) AG N0
Note: Award no marks if the only working seen is \({\text{A}}{{\text{C}}^2} = 49\) or \({\text{AC}} = \sqrt {49} \) (or similar).
[4 marks]
correct substitution for semicircle (A1)
eg\(\,\,\,\,\,\)\({\text{semicircle}} = \frac{1}{2}(2\pi \times 3.5),{\text{ }}\frac{1}{2} \times \pi \times 7,{\text{ }}3.5\pi \)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{perimeter}} = {\text{AB}} + {\text{BC}} + {\text{semicircle, }}3 + 8 + \left( {\frac{1}{2} \times 2 \times \pi \times \frac{7}{2}} \right),{\text{ }}8 + 3 + 3.5\pi \)
\(11 + \frac{7}{2}\pi {\text{ }}( = 3.5\pi + 11){\text{ (cm)}}\) A1 N2
[3 marks]
Question
[Maximum mark: 8] [with / without GDC]
O is the centre of the circle which has a radius of 10 cm. The size of AÔB is 1.5 rad.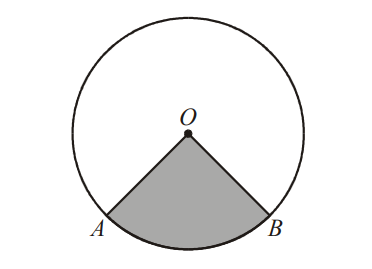
(a) Find the lengths of the minor arc AB and of the major arc AB. [3]
(b) Find the areas of the minor sector (shaded region) and of the major sector. [3]
(c) Find the perimeters of the minor sector (shaded region) and of the major sector. [2]
Answer/Explanation
Ans:
(a) \(l_{\text {MINOR }}=(10)(1.5)=15 \quad l_{\text {MAJOR }}=(10)(2 \pi-1.5)=20 \pi-15\)
(b) \(A_{M I N O R}=\frac{1}{2}(10)^{2}(1.5)=75 \quad A_{M A J O R}=\frac{1}{2}(10)^{2}(2 \pi-1.5)=200 \pi-75\)
(c) \(P_{\text {MINOR }}=l_{\text {MINOR }}+2 r=35 \quad P_{\text {MAJOR }}=l_{\text {MAJOR }}+2 r=20 \pi+5\)
Question
[Maximum mark: 6] [without GDC]
The diagram below shows a triangle and two arcs of circles.
The triangle ABC is a right-angled isosceles triangle, with AB = AC = 2. The point P is the midpoint of [BC].
The arc BDC is part of a circle with centre A.
The arc BEC is part of a circle with centre P.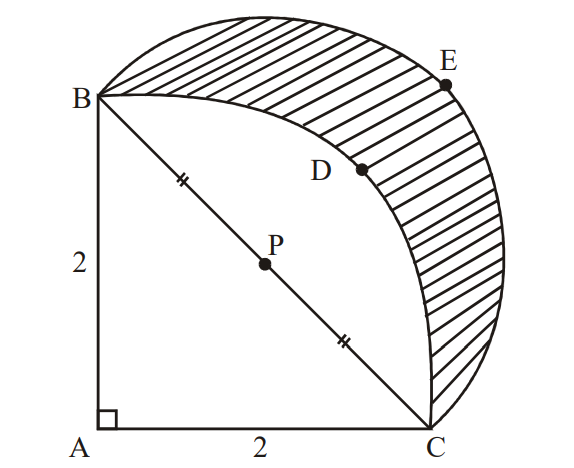
(a) Calculate the area of the segment BDCP. [3]
(b) Calculate the area of the shaded region BECD. [3]
Answer/Explanation
Ans:
(a) area of sector ΑΒDC = \(\frac{1}{4} \pi(2)^{2}=\pi\)
area of segment BDCP = π – area of \(\Delta\)ABC = π – 2
(b) \(\mathrm{BP}=\sqrt{2}\)
area of semicircle of radius BP = \(\frac{1}{2} \pi(\sqrt{2})^{2}=\pi\)
area of shaded region = π – (π – 2) = 2