Question
(a) Show that the equation cos2x = sin x can be written in the form \(2sin^2\) x + sin x – 1 = 0.
(b) Hence, solve cos2x = sin x, where -π ≤ x ≤ π.
Answer/Explanation
Answer:
(a) \(1 – 2sin^2x = sin x\)
\(2 sin^2 x + sin x – 1 = 0\)
(b) valid attempt to solve quadratic
(2sin x – 1)(sin x + 1) OR \(\frac{-1 ± \sqrt{1-4(2)(-1)}}{2(2)}\)
recognition to solve for sin x
sin \(x = \frac{1}{2}\) OR sin x = -1
any correct solution from sin x = -1
any correct solution from sin \(x = \frac{1}{2}\)
x = -\(\frac{\pi}{2}, \frac{\pi}{6}, \frac{5 \pi}{6}\)
Question
Given that \(\cos A = \frac{1}{3}\) and \(0 \le A \le \frac{\pi }{2}\) , find \(\cos 2A\) .[3]
Given that \(\sin B = \frac{2}{3}\) and \(\frac{\pi }{2} \le B \le \pi \) , find \(\cos B\) .[3]
Answer/Explanation
Markscheme
evidence of choosing the formula \(\cos 2A = 2{\cos ^2}A – 1\) (M1)
Note: If they choose another correct formula, do not award the M1 unless there is evidence of finding \({\sin ^2}A = 1 – \frac{1}{9}\)
correct substitution A1
e.g.\(\cos 2A = {\left( {\frac{1}{3}} \right)^2} – \frac{8}{9}\) , \(\cos 2A = 2 \times {\left( {\frac{1}{3}} \right)^2} – 1\)
\(\cos 2A = – \frac{7}{9}\) A1 N2
[3 marks]
METHOD 1
evidence of using \({\sin ^2}B + {\cos ^2}B = 1\) (M1)
e.g. \({\left( {\frac{2}{3}} \right)^2} + {\cos ^2}B = 1\) , \(\sqrt {\frac{5}{9}} \) (seen anywhere),
\(\cos B = \pm \sqrt {\frac{5}{9}} \) \(\left( { = \pm \frac{{\sqrt 5 }}{3}} \right)\) (A1)
\(\cos B = – \sqrt {\frac{5}{9}} \) \(\left( { = – \frac{{\sqrt 5 }}{3}} \right)\) A1 N2
METHOD 2
diagram M1
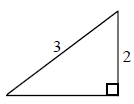
for finding third side equals \(\sqrt 5 \) (A1)
\(\cos B = – \frac{{\sqrt 5 }}{3}\) A1 N2
[3 marks]
Question
Solve \(\cos 2x – 3\cos x – 3 – {\cos ^2}x = {\sin ^2}x\) , for \(0 \le x \le 2\pi \) .
Answer/Explanation
Markscheme
evidence of substituting for \(\cos 2x\) (M1)
evidence of substituting into \({\sin ^2}x + {\cos ^2}x = 1\) (M1)
correct equation in terms of \(\cos x\) (seen anywhere) A1
e.g. \(2{\cos ^2}x – 1 – 3\cos x – 3 = 1\) , \(2{\cos ^2}x – 3\cos x – 5 = 0\)
evidence of appropriate approach to solve (M1)
e.g. factorizing, quadratic formula
appropriate working A1
e.g. \((2\cos x – 5)(\cos x + 1) = 0\) , \((2x – 5)(x + 1)\) , \(\cos x = \frac{{3 \pm \sqrt {49}}}{4}\)
correct solutions to the equation
e.g. \(\cos x = \frac{5}{2}\) , \(\cos x = – 1\) , \(x = \frac{5}{2}\) , \(x = – 1\) (A1)
\(x = \pi \) A1 N4
[7 marks]
Question
Let \(f(x) = \cos 2x\) and \(g(x) = 2{x^2} – 1\) .
Find \(f\left( {\frac{\pi }{2}} \right)\) .[2]
Find \((g \circ f)\left( {\frac{\pi }{2}} \right)\) .[2]
Given that \((g \circ f)(x)\) can be written as \(\cos (kx)\) , find the value of k, \(k \in \mathbb{Z}\) .[3]
Answer/Explanation
Markscheme
\(f\left( {\frac{\pi }{2}} \right) = \cos \pi \) (A1)
\( = – 1\) A1 N2
[2 marks]
\((g \circ f)\left( {\frac{\pi }{2}} \right) = g( – 1)\) \(( = 2{( – 1)^2} – 1)\) (A1)
\(= 1\) A1 N2
[2 marks]
\((g \circ f)(x) = 2{(\cos (2x))^2} – 1\) \(( = 2{\cos ^2}(2x) – 1)\) A1
evidence of \(2{\cos ^2}\theta – 1 = \cos 2\theta \) (seen anywhere) (M1)
\((g \circ f)(x) = \cos 4x\)
\(k = 4\) A1 N2
[3 marks]