Question
The following diagram shows the graph of \(f(x) = a\cos (bx)\) , for \(0 \le x \le 4\) .
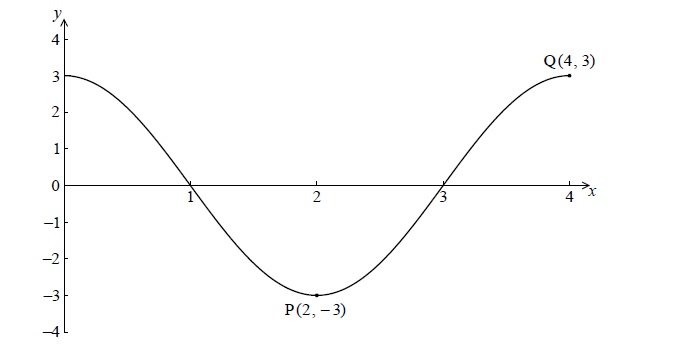
There is a minimum point at P(2, − 3) and a maximum point at Q(4, 3) .
(i) Write down the value of a .
(ii) Find the value of b .
Write down the gradient of the curve at P.
Write down the equation of the normal to the curve at P.
Answer/Explanation
Markscheme
(i) \(a = 3\) A1 N1
(ii) METHOD 1
attempt to find period (M1)
e.g. 4 , \(b = 4\) , \(\frac{{2\pi }}{b}\)
\(b = \frac{{2\pi }}{4}\left( { = \frac{\pi }{2}} \right)\) A1 N2
[3 marks]
METHOD 2
attempt to substitute coordinates (M1)
e.g. \(3\cos (2b) = – 3\) , \(3\cos (4b) = 3\)
\(b = \frac{{2\pi }}{4}\left( { = \frac{\pi }{2}} \right)\) A1 N2
[3 marks]
0 A1 N1
[1 mark]
recognizing that normal is perpendicular to tangent (M1)
e.g. \({m_1} \times {m_2} = – 1\) , \(m = – \frac{1}{0}\) , sketch of vertical line on diagram
\(x = 2\) (do not accept 2 or \(y = 2\) ) A1 N2
[2 marks]
Question
[Maximum mark: 12] [without GDC]
Part of the graph of a trigonometric function f(x) is given below. There is a local maximum at (π/8,180) and a local minimum at (3π/8,20).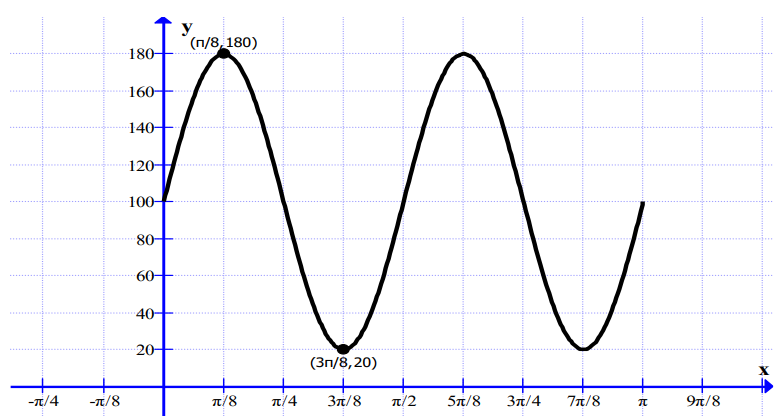
(a) Write down the values of
(i) the amplitude (ii) the central value (iii) the period [3]
(b) Express the function in the form f (x) = Asin Bx + C [3]
(c) Complete the following table by expressing f (x) in three alternative forms [6]
Answer/Explanation
Ans:
(a) amplitude = 80, central value = 100, period = π/2
(b) f(x) = 80sin 4x + 100, since \(B=\frac{2 \pi}{\text { Period }}=\frac{2 \pi}{\pi / 2}=4\)
(c) (i) \(f(x)=-80 \sin 4\left(x-\frac{\pi}{4}\right)+100\) (\(D=\frac{\pi}{4}\) is the position of the 2nd (↓) root)
(ii) \(f(x)=80 \cos 4\left(x-\frac{\pi}{8}\right)+100\) (\(D=\frac{\pi}{8}\) is the position of the maximum)
(iii) \(f(x)=-80 \cos 4\left(x-\frac{3 \pi}{8}\right)+100\) (\(D=\frac{3 \pi}{8}\) is the position of the minimum)