Question
The function f is defined by f (x) = sinqx , where q > 0. The following diagram shows part of the graph of f for 0 ≤ x ≤ 4m, where x is in radians. There are x-intercepts at x = 0, 2m and 4m.
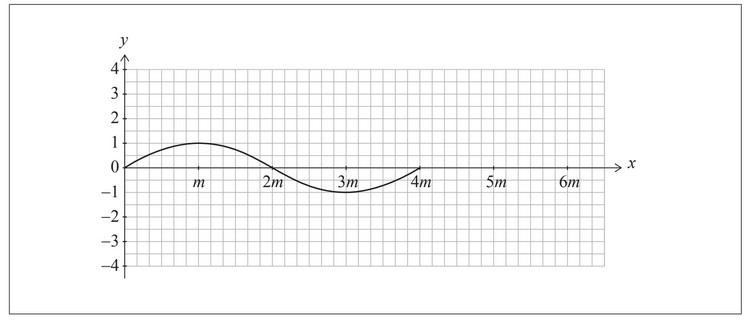
(a) Find an expression for m in terms of q.
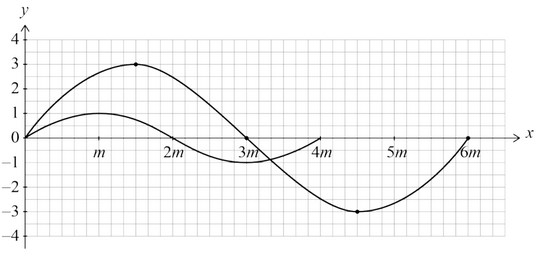
The function g is defined by g (x) = 3 sin\(\frac{2qx}{3}\), for 0 ≤ x ≤ 6m.
(b) On the axes above, sketch the graph of g.
Answer/Explanation
Answer:
(a) recognition that period is 4m OR substitution of a point on f (except the origin)
\(4m = \frac{2 \pi}{q}\) OR 1 = sin qm
\(m = \frac{\pi}{2q}\)
(b) horizontal scale factor is \(\frac{3}{2}\) (seen anywhere)
Question
Find the least positive value of x for which
\(cos\left ( \frac{x}{2}+\frac{\pi}{3} \right )=\frac{1}{\sqrt{2}}\)
Answer/Explanation
Ans

Question
Show that sin \(\frac{sinxtanx}{1-cosx}= 1+\frac{1}{cosx}\) x ≠ 2nπ, n ∈ R . [3]
Hence determine the range of values of k for which \(\frac{sinxtanx}{1-cosx}\)= K has no real solutions. [4]
Answer/Explanation
Ans:
(a)
METHOD 1
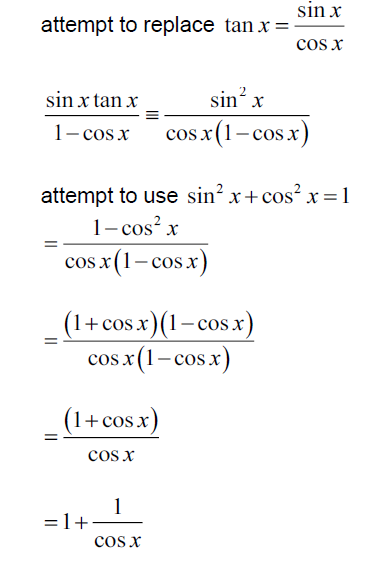
METHOD 2
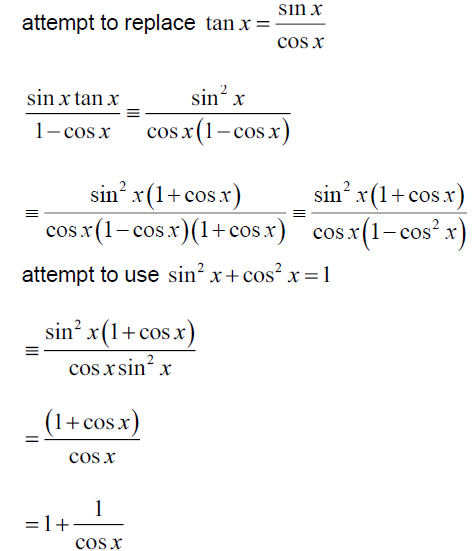
(b)
METHOD 1
consider \(1+\frac{1}{cosx}\)= k, leasing to cosx= \(\frac{1}{k-1}\)
consider graoh of y= \(\frac{1}{y-1}\)or range of solutions for y= cosx
(no solutions if y<-1or y>1)\(\Rightarrow 0<k<2\)
METHOD 2
consider graph of y= 1+ sec x
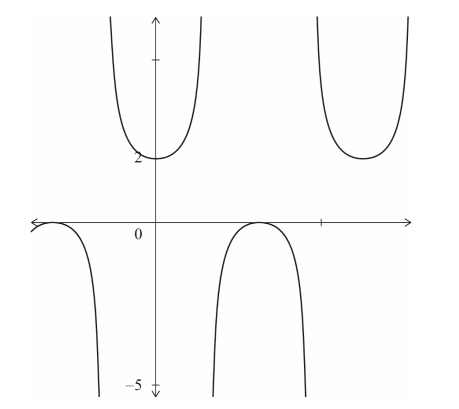
no real solutions if 0<k<2
METHOD 3
Question
Consider the function f defined by f (x) = 6 + 6 cos x , for 0 ≤ x ≤ 4π .
The following diagram shows the graph of y = f (x) .
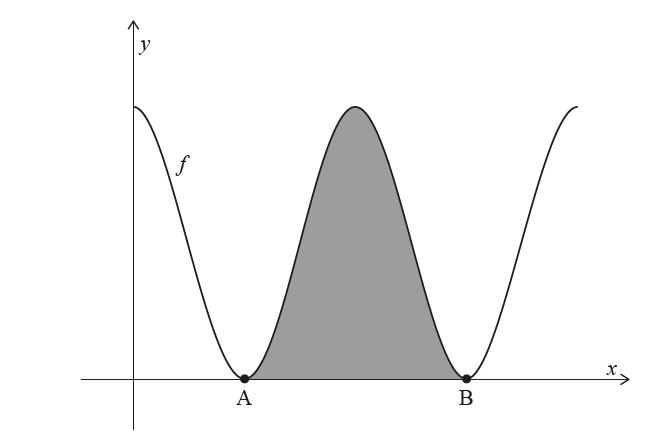
The graph of f touches the x-axis at points A and B, as shown. The shaded region is enclosed by the graph of y = f (x) and the x-axis, between the points A and B.
(a) Find the x-coordinates of A and B. [3]
(b) Show that the area of the shaded region is 12π . [5]
The right cone in the following diagram has a total surface area of 12π , equal to the shaded area in the previous diagram.
The cone has a base radius of 2, height h , and slant height l .
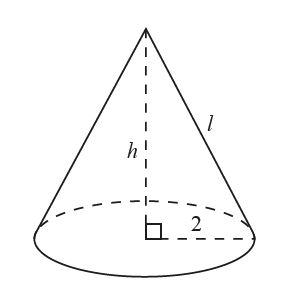
(c) Find the value of l . [3]
(d) Hence, find the volume of the cone. [4]
Answer/Explanation
Ans:
(a) When $f\left(x\right)=0$,
$$\begin{eqnarray}
6\left(1+\cos x\right) = 0 \nonumber \\
\cos x = -1.
\end{eqnarray}$$
Thus, $x=\pi$ or $x=3\pi$.<br>
(b)
$$\begin{eqnarray}
\text{req’d area} &=& \int_{\pi}^{3\pi} f\left(x\right) \text{d}x \nonumber \\
&=& 6\int_{\pi}^{3\pi} 1+\cos x \text{d}x \nonumber \\
&=& 6\left[ 1+\sin x \right]_{\pi}^{3\pi} \nonumber \\
&=& 6\left(3\pi-\pi\right) \nonumber \\
&=& 12\pi.
\end{eqnarray}$$
(c)
$$\begin{eqnarray}
\text{total surface area} &=& \pi\left(2\right)^2+\pi\left(2\right)l \nonumber \\
12\pi &=& 4\pi+2\pi l \nonumber \\
2\pi l &=& 8\pi \nonumber \\
l &=& 4.
\end{eqnarray}$$
(d) By Pythagoras’ Theorem, we have $h=\sqrt{4^2-2^2}$, i.e., $h=\sqrt{12}$. Thus,
$$\begin{eqnarray}
\text{vol. of cone} &=& \frac{1}{3}\pi\left(2\right)^2\left(h\right) \nonumber \\
&=& \frac{4\pi\sqrt{12}}{3} \nonumber \\
&=& \frac{8\pi\sqrt{3}}{3}.
\end{eqnarray}$$
Question
Solve the equation 2 cos2 x + 5 sin x = 4 , 0 ≤ x ≤ 2π . [Maximum mark: 7]
Answer/Explanation
Ans:
2cos2x+5sinx=4
2(1−sin2x)+5sinx=4
2sin2x−5sinx+2=0
(2sinx−1)(sinx−2)=0.
Thus, sinx=1/2 or sinx=2 (no solution)
For sinx=1/2, we have α=arcsin1/2=π/6. Since 0≤x≤2π, x=π/6 or x=5π/6.
Question
Let f(x) = cos 2x + cos x + 1 and g(x) = sin 2x + sin x.
Solve the following equations in the interval 0≤x≤2\(\pi\)
(a) f(x) = 0 (b) g(x) = 0 (c) f(x) = g(x)
Answer/Explanation
Ans
We use double angle formulas to simplify the expressions
(a) \(x=\frac{\pi}{2},x=\frac{2\pi}{3},x=\frac{4\pi}{3},x=\frac{3\pi}{2}\)
(b) \(x=0,x=\frac{2\pi}{3},x=\pi,x=\frac{4\pi}{3},x=2\pi\)
(c) \(x=\frac{\pi}{4},x=\frac{2\pi}{3},x=\frac{5\pi}{4},x-\frac{4\pi}{3}\)