Question
Let \(f(x) = {(\sin x + \cos x)^2}\) .
Show that \(f(x)\) can be expressed as \(1 + \sin 2x\) .[2]
The graph of f is shown below for \(0 \le x \le 2\pi \) .
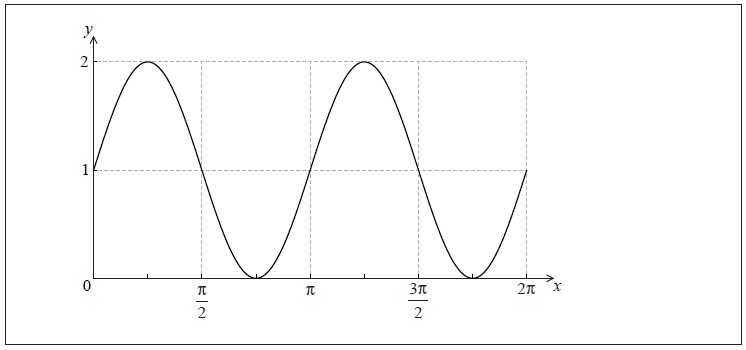
Let \(g(x) = 1 + \cos x\) . On the same set of axes, sketch the graph of g for \(0 \le x \le 2\pi \) .[2]
The graph of g can be obtained from the graph of f under a horizontal stretch of scale factor p followed by a translation by the vector \(\left( {\begin{array}{*{20}{c}}
k\\
0
\end{array}} \right)\) .
Write down the value of p and a possible value of k .[2]
Answer/Explanation
Markscheme
attempt to expand (M1)
e.g. \((\sin x + \cos x)(\sin x + \cos x)\) ; at least 3 terms
correct expansion A1
e.g. \({\sin ^2}x + 2\sin x\cos x + {\cos ^2}x\)
\(f(x) = 1 + \sin 2x\) AG N0
[2 marks]
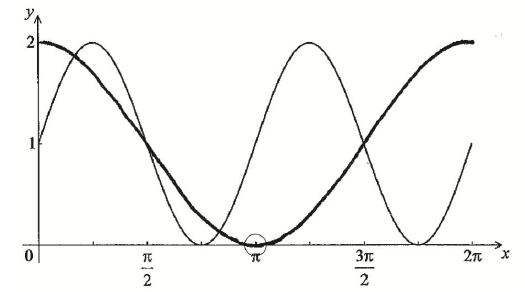A1A1 N2
Note: Award A1 for correct sinusoidal shape with period \(2\pi \) and range \([0{\text{, }}2]\), A1 for minimum in circle.
\(p = 2\) , \(k = – \frac{\pi }{2}\) A1A1 N2
[2 marks]
Question
Let \(f(x) = {\sin ^3}x + {\cos ^3}x\tan x,\frac{\pi }{2} < x < \pi \) .
Show that \(f(x) = \sin x\) .[2]
Let \(\sin x = \frac{2}{3}\) . Show that \(f(2x) = – \frac{{4\sqrt 5 }}{9}\) .[5]
Answer/Explanation
Markscheme
changing \(\tan x\) into \(\frac{{\sin x}}{{\cos x}}\) A1
e.g. \({\sin ^3}x + {\cos ^3}x\frac{{\sin x}}{{\cos x}}\)
simplifying A1
e.g \(\sin x({\sin ^2}x + {\cos ^2}x)\) , \({\sin ^3}x + \sin x – {\sin ^3}x\)
\(f(x) = \sin x\) AG N0
[2 marks]
recognizing \(f(2x) = \sin 2x\) , seen anywhere (A1)
evidence of using double angle identity \(\sin (2x) = 2\sin x\cos x\) , seen anywhere (M1)
evidence of using Pythagoras with \(\sin x = \frac{2}{3}\) M1
e.g. sketch of right triangle, \({\sin ^2}x + {\cos ^2}x = 1\)
\(\cos x = – \frac{{\sqrt 5 }}{3}\) (accept \(\frac{{\sqrt 5 }}{3}\) ) (A1)
\(f(2x) = 2\left( {\frac{2}{3}} \right)\left( { – \frac{{\sqrt 5 }}{3}} \right)\) A1
\(f(2x) = – \frac{{4\sqrt 5 }}{9}\) AG N0
[5 marks]
Question
The following diagram shows a right-angled triangle, \(\rm{ABC}\), where \(\sin \rm{A} = \frac{5}{{13}}\).
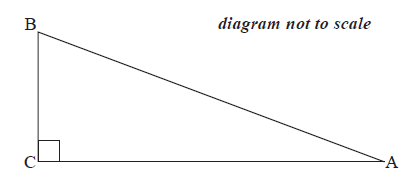
Show that \(\cos A = \frac{{12}}{{13}}\).[2]
Find \(\cos 2A\).[3]
Answer/Explanation
Markscheme
METHOD 1
approach involving Pythagoras’ theorem (M1)
eg \({5^2} + {x^2} = {13^2}\), labelling correct sides on triangle
finding third side is 12 (may be seen on diagram) A1
\(\cos A = \frac{{12}}{{13}}\) AG N0
METHOD 2
approach involving \({\sin ^2}\theta + {\cos ^2}\theta = 1\) (M1)
eg \({\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\theta = 1,{\text{ }}{x^2} + \frac{{25}}{{169}} = 1\)
correct working A1
eg \({\cos ^2}\theta = \frac{{144}}{{169}}\)
\(\cos A = \frac{{12}}{{13}}\) AG N0
[2 marks]
correct substitution into \(\cos 2\theta \) (A1)
eg \(1 – 2{\left( {\frac{5}{{13}}} \right)^2},{\text{ }}2{\left( {\frac{{12}}{{13}}} \right)^2} – 1,{\text{ }}{\left( {\frac{{12}}{{13}}} \right)^2} – {\left( {\frac{5}{{13}}} \right)^2}\)
correct working (A1)
eg \(1 – \frac{{50}}{{169}},{\text{ }}\frac{{288}}{{169}} – 1,{\text{ }}\frac{{144}}{{169}} – \frac{{25}}{{169}}\)
\(\cos 2A = \frac{{119}}{{169}}\) A1 N2
[3 marks]