3.1 Thermal concepts
Essential Idea:
Thermal physics deftly demonstrates the links between the macroscopic measurements essential to many scientific models with the microscopic properties
that underlie these models.
Understandings:
- Molecular theory of solids, liquids and gases
- Temperature and absolute temperature
- Internal energy
- Specific heat capacity
- Phase change
- Specific latent heat
Applications and Skills:
- Describing temperature change in terms of internal energy
- Using Kelvin and Celsius temperature scales and converting between them
- Applying the calorimetric techniques of specific heat capacity or specific latent heat experimentally
- Describing phase change in terms of molecular behaviour
- Sketching and interpreting phase change graphs
- Calculating energy changes involving specific heat capacity and specific latent heat of fusion and vaporization
- • The macroscopic effects of volume, pressure, and temperature can be understood with a microscopic model
- • Kinetic Energy on a molecular level is observed as temperature and heat
- • The heat required to change the temperature or phase of a material is a property of the material itself
- • The properties of are proportional to each other for an ideal gas and can be calculated under certain conditions
Content Objectives
Heat vs Temperature
- I can explain the relationship between temperature and molecular kinetic energy
- I can describe the energies present in an object’s total internal energy
- I can convert between Fahrenheit, Celsius, and Kelvin
- I can describe the nature of molecules when at a temperature of absolute zero
- I can compare temperature (average KE) and heat (total KE)
- I can describe the molecular process that allows heat to flow
Specific Heat
- I can define specific heat capacity with proper units
- I can describe the effect of larger or smaller specific heat values
- I can relate specific heat capacity to the heat energy and temperature change
- I can describe how a calorimeter uses the conservation of heat to study a material’s specific heat
- I can experimentally determine the specific heat capacity of a material
Latent Heat
- I can identify key features in a material’s heating curve
- I can describe why a heating curve plateaus during phase changes
- I can describe the different ways that the heat added to a system can become internal energy
- I can define specific latent heat with proper units
- I can calculate the heat required to cause a certain amount of a substance to change phases
- I can compare the processes of evaporation and boiling
Kinetic Gas Theory
- I can describe the conditions necessary for a substance to be considered an ideal gas
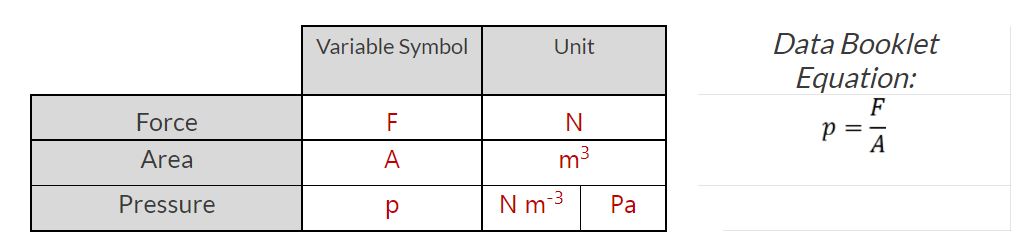
- I can define pressure with appropriate fundamental and derived units
- I can relate average molecular kinetic energy with absolute temperature
- I can calculate the average molecule speed for a molecule at a certain temperature
- I can discuss how the mass of a molecule changes its overall speed at a given temperature
The Mole
- I can describe the importance of having a large quantity like the “mole” defined
- I can identify the difference between different isotopes of an element
- I can calculate an atom’s mass number when given the number of protons and neutrons
- I can use the average atomic weight of an element to convert between mass and moles
Gas Laws
- I can identify conditions when a substance is no longer considered an ideal gas
- I can describe the relationship between volume and pressure for an ideal gas (Boyle’s Law)
- I can describe the relationship between temperature and pressure for an ideal gas (Pressure Law)
- I can describe the relationship between temperature and volume for an ideal gas (Charles’s Law)
- I can use the Ideal Gas Law to solve for pressure, volume, amount, or temperature
- I can use the Ideal Gas Law to describe how changing one or more variable(s) would affect another
Thermal Concept Summary
 |  |
Specific Heat Capacity and Specific Latent Heat
 |  |
Heating Curves
 |  |
Pressure
Kinetic Theory and Temperature
Ideal Gas Law

Ideal Gas Relationships
 |  |  |
Particle model of matter
Macroscopic world VS. microscopic world
Matter is consisted of small structures: Molecules…Atoms…Quarks, known as Particles.
Inter-particle forces: “Spring-like” bonds between particles.
Bond force: Solid (s) > Liquid (l) > Gas (g) – phases of matter.
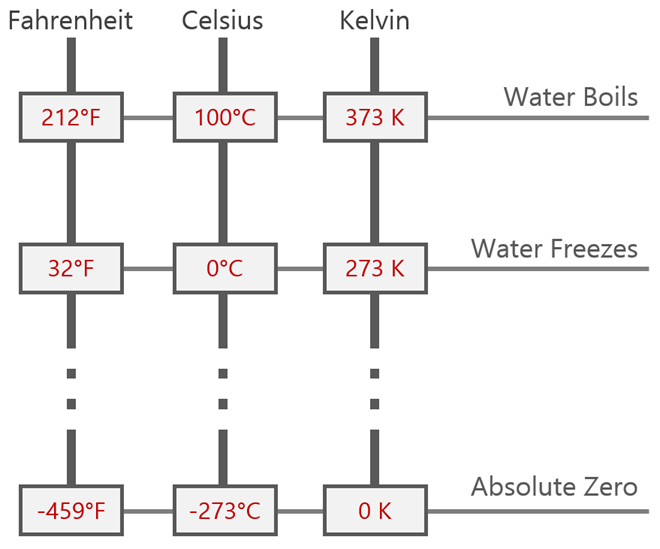
Absolute temperature
“Absolute temperature is proportional to the average random kinetic of the molecules”.
Absolute temperature = T (in kelvin, K) = Temperature in degrees Celsius (ºC) + 273
Absolute zero (0 K): Zero Kinetic energy (theoretically).
Triplet point of water (273 K): water can be in any of the 3 phases.
Internal energy
“The internal energy of a substance is the total potential energy (due to inter-molecular bonds between particles) and the total random kinetic energy of all the molecules in the substance.” It can change as a result from heat added or taken and work performed.
Kinetic energy of particles: translational kinetic energy + rotational kinetic energy.
Heat energy = Thermal energy: “Heat energy that is transferred from one body to another as a result of a difference in temperature until thermal equilibrium”.
Direction of energy transfer: From body with higher temperature to body with lower temperature.
Thermal concepts and phase changes
Specific heat capacity (c): “Energy required to increase the temperature of a units mass of a certain substance by one kelvin.”
- Q = mc∆T (always positive!)
Thermal capacity (C): “Energy required to raise 1 K of an object (e.g. a container)”.
Specific latent heat (L): “Energy required to change the phase of a unit mass at constant temperature.”
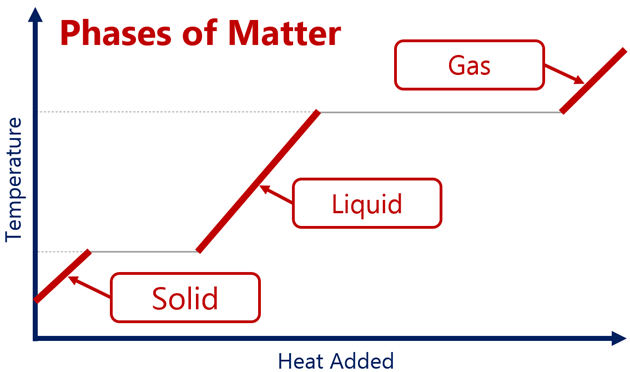
During a phase change, the temperature does not change, as the kinetic energy does not increase, only the potential energy increases.
Q = mL (always positive!)
Rate of thermal energy transfer is increased by increasing the difference between the temperatures of a body and that of the surroundings and increasing the surface area.
Temperature of a substance changing with time, with energy being supplied by a constant power source:
* Vaporization is different than evaporation – the latter depends on surface area
The method of mixtures
Assumptions: no heat transferred to the surroundings/to the container, substance heated uniformly.
THERMAL PROPERTIES OF MATTER
TEMPERATURE
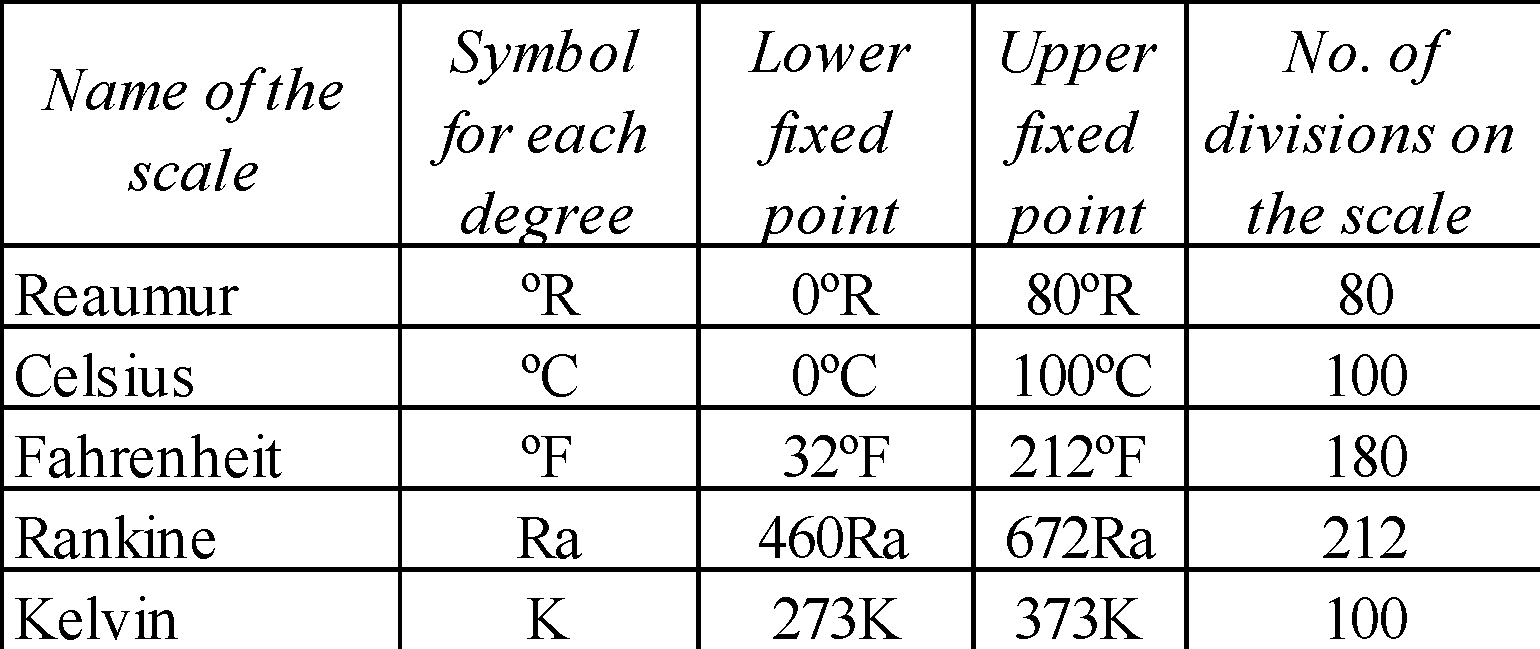
- Lower fixed point (LFP) is the freezing point of water.
- Upper fixed point (UFP) is the boiling point of water.
IDEAL GAS EQUATION
- Boyle’s law : When temperature is held constant, the pressure is inversely proportional to volume.
- Charle’s law : When the pressure is held constant, the volume of the gas is directly proportional to the absolute temperature.
- Avogadro’s law : When the pressure and temperature are kept constant, the volume is directly proportional to the number of moles of the ideal gas in the container.
ABSOLUTE TEMPERATURE
- The mercury thermometer with cylindrical bulb are more sensitive than those with spherical bulb.
- Alcohol thermometer is preferred to the mercury thermometer due to the larger value of the coefficient of cubical expansion.
- Properties that make mercury the ideal thermometric substance are :
- It does not stick to the glass walls
- Available in pure form
- Low thermal conductivity and low specific heat
- Vapour Pressure is low
- Coefficient of expansion is uniform
- It shines
- Gas thermometer is more sensitive than the mercury thermometer, because its coefficient of cubical expansion is much larger.
- At the following temperatures different temperature scales have the same reading :
- Fahrenheit and Reaumur at –25.6ºF = –25.6ºR
- Reaumur and Celsius at 0ºR = OºC
- Celsius and Fahrenheit at –40ºC = –40ºF
- Fahrenheit and Kelvin at 574.25ºF = 574.25K
- The Celsius scale and the Kelvin cannot have the same reading at any temperature.
- Six’s thermometer measures minimum and maximum temperature during a day. It uses mercury as well as alcohol as the thermometric substances.
- Normal human body temperature is 37ºC = 98.6ºF.
- Clinical thermometers are much shorter than the laboratory thermometers because they are used to measure a limited range (96º F to 100º F) of temperature.
- Rapidly changing temperature is measured by using thermo electric thermometer.
- The temperature inside a motor engine is measured using platinum resistance thermometer.
- The radiation thermometers can measure temperature from a distance.
- Adiabatic demagnetisation can be used to measure temperature very near to the absolute zero.
- The Rankine is the smallest temperature range among all the scales of temperature.
- When a substance is heated it expands along each dimension in the same proportion. (if it is uniform)
THERMAL EXPANSION
THERMAL EXPANSION OF SUBSTANCES
i.e., increase in length with increase in temperature
i.e., increase in area with increase in temperature.
i.e. increase in volume with increase in temperature.
- During change in temperature, the mass does not change but the density decreases due to increase in volume. Therefore
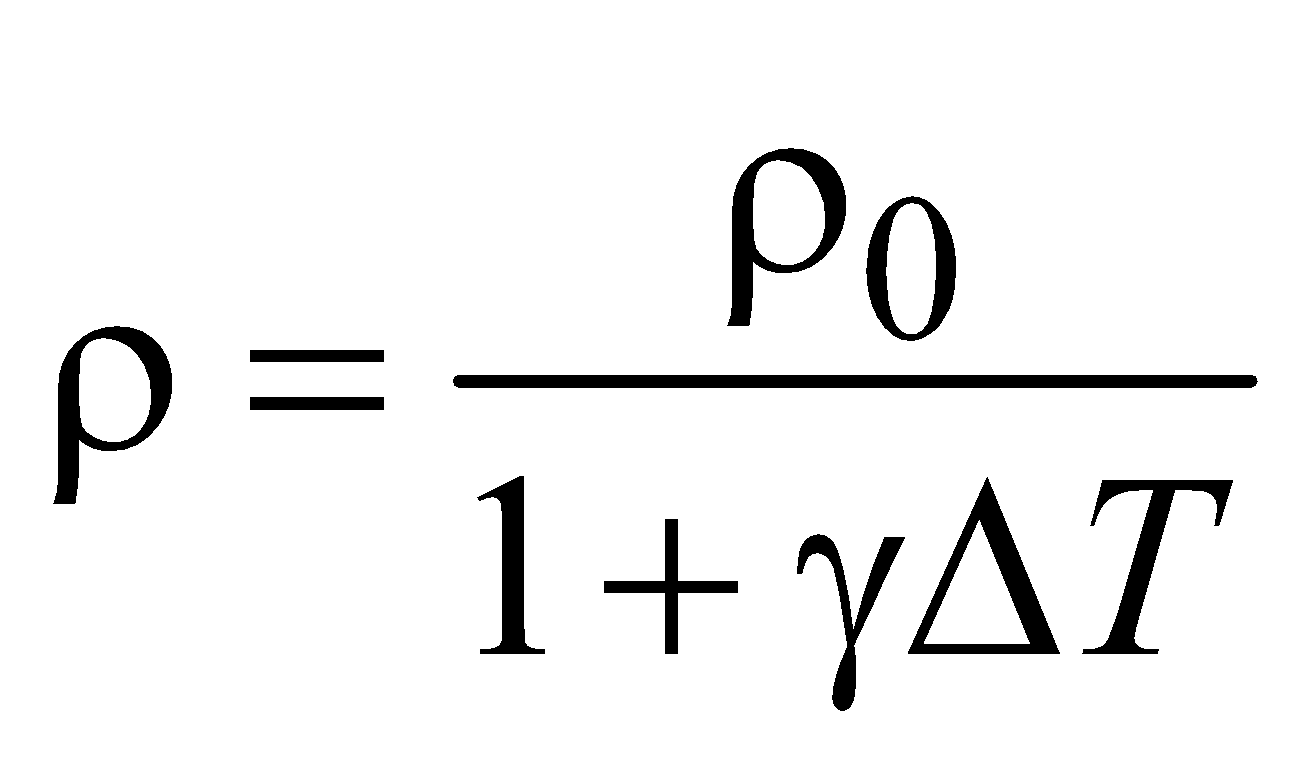
- Relation between α, β and γ
- Water has negative coefficient of volume expansion for temperature range (0°C – 4°C). Therefore water contracts when the temperature rises from 0°C to 4°C and then expands as the temperature increases further.
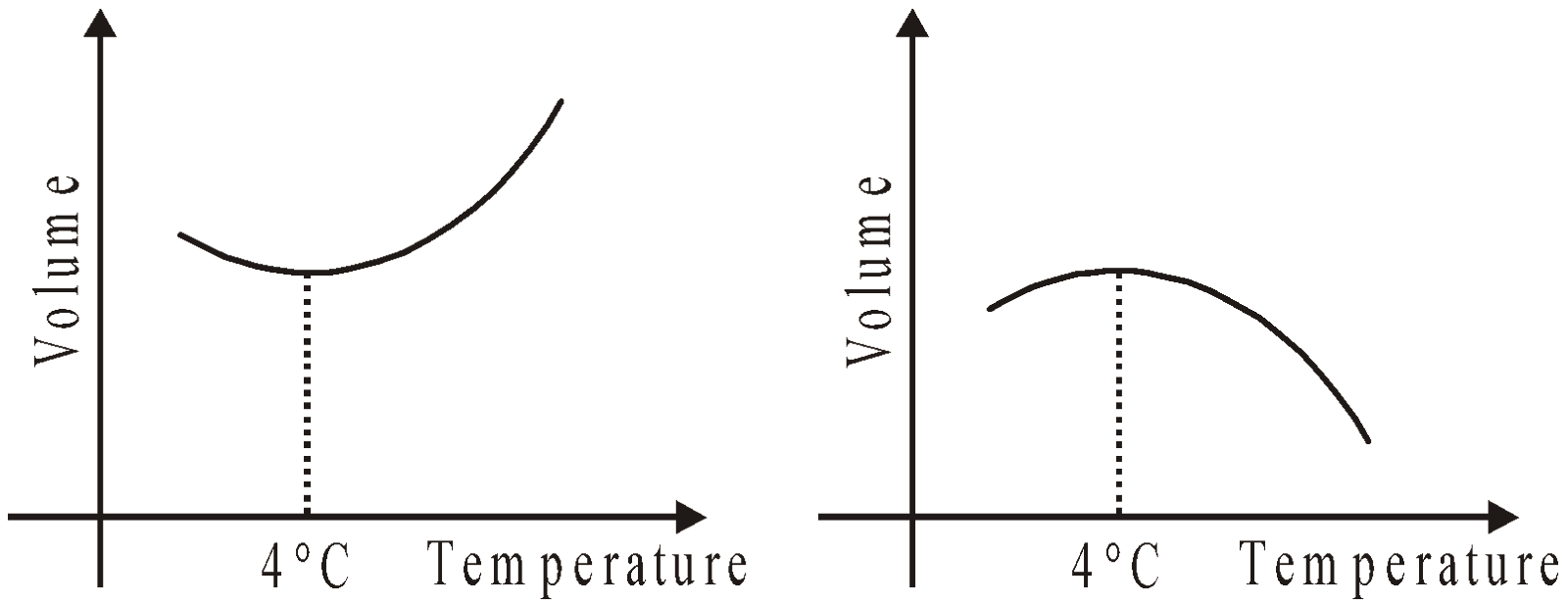
THERMAL EXPANSION OF LIQUID (WHICH IS HEATED IN A VESSEL)
It is clear from the formula that
if
if
CHANGE IN DENSITY OF SOLIDS AND LIQUIDS WITH TEMPERATURE
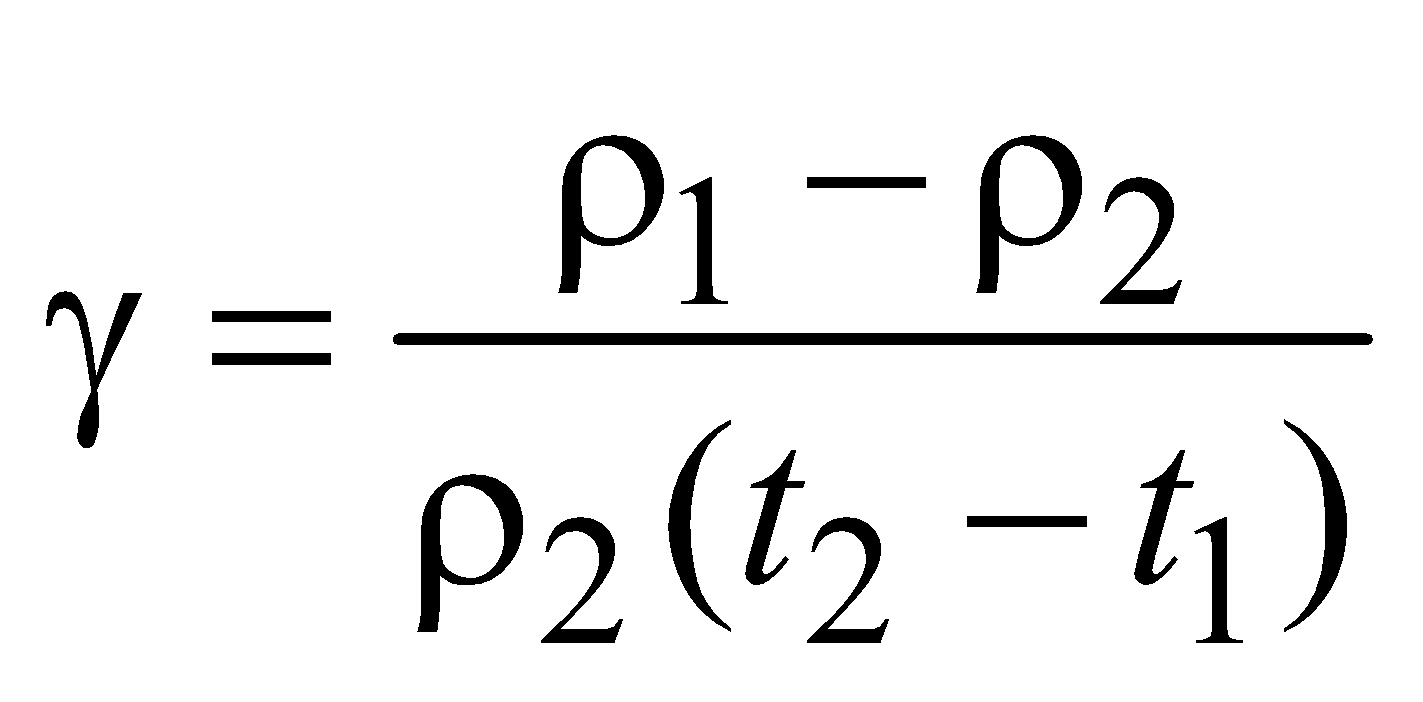
THERMAL STRESS
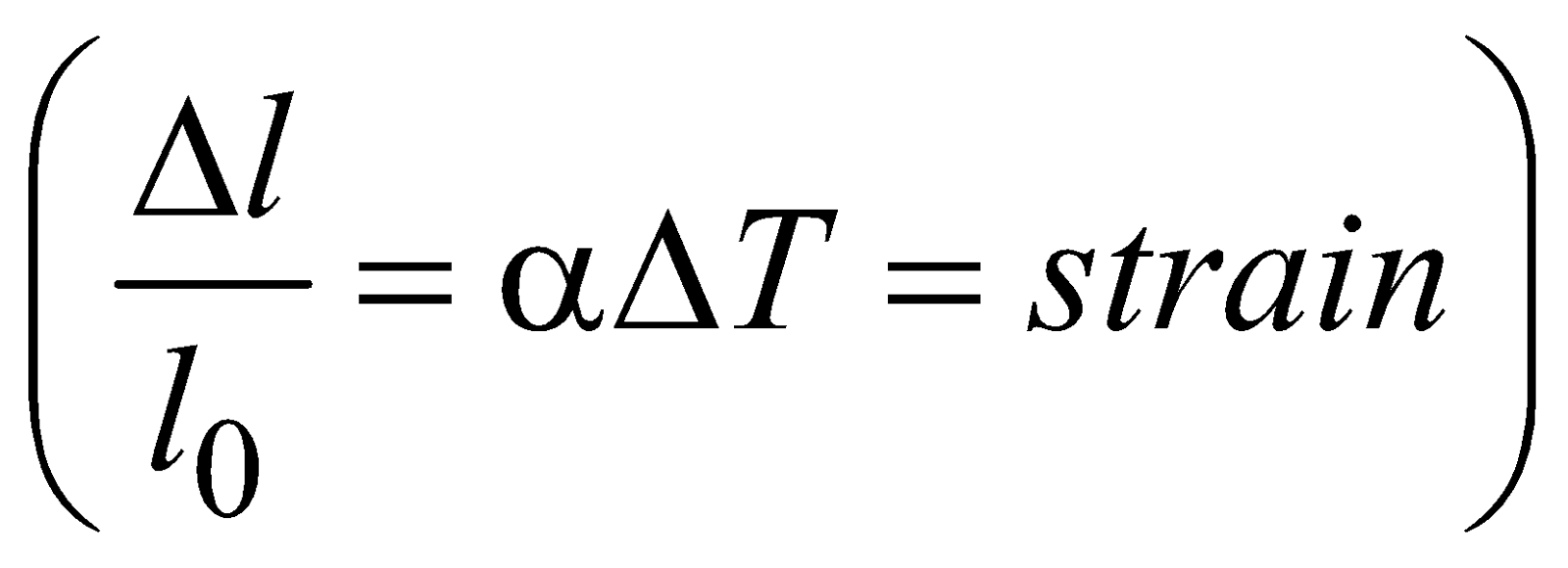
EFFECT OF TEMPERATURE ON PENDULUM CLOCK
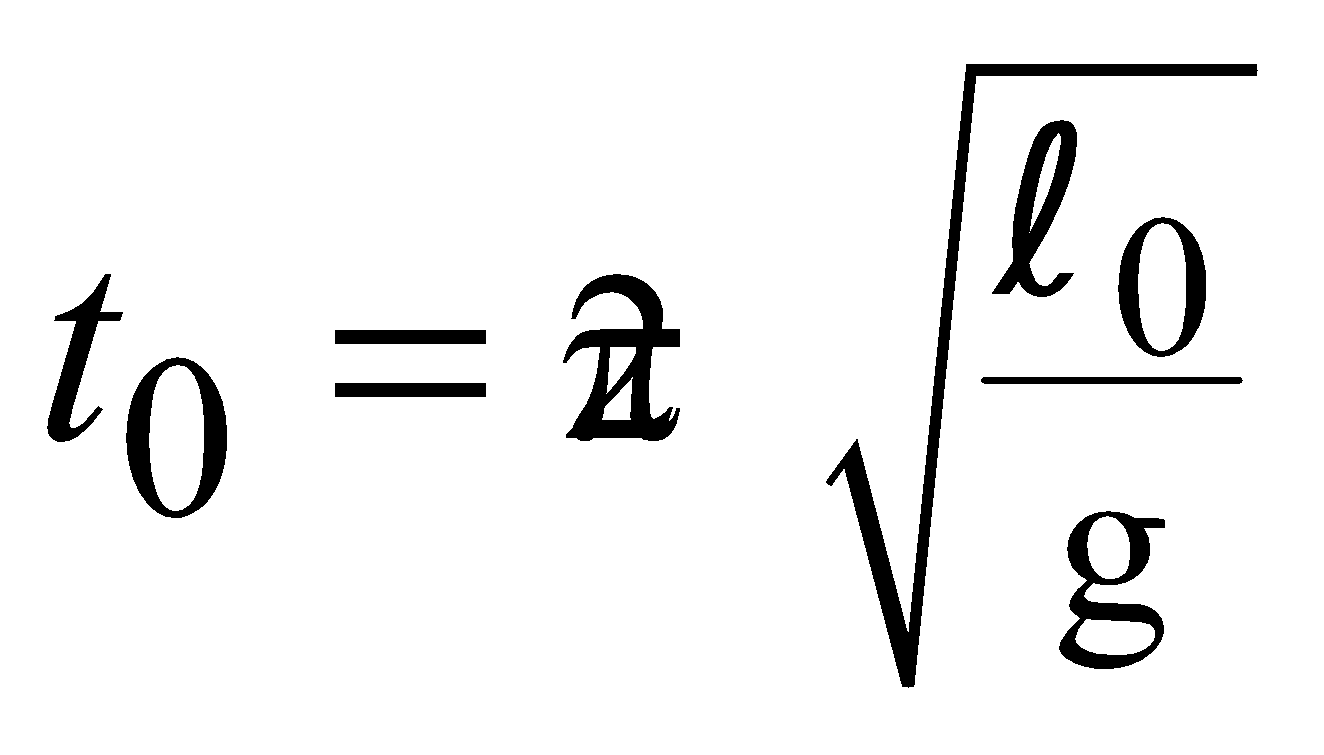
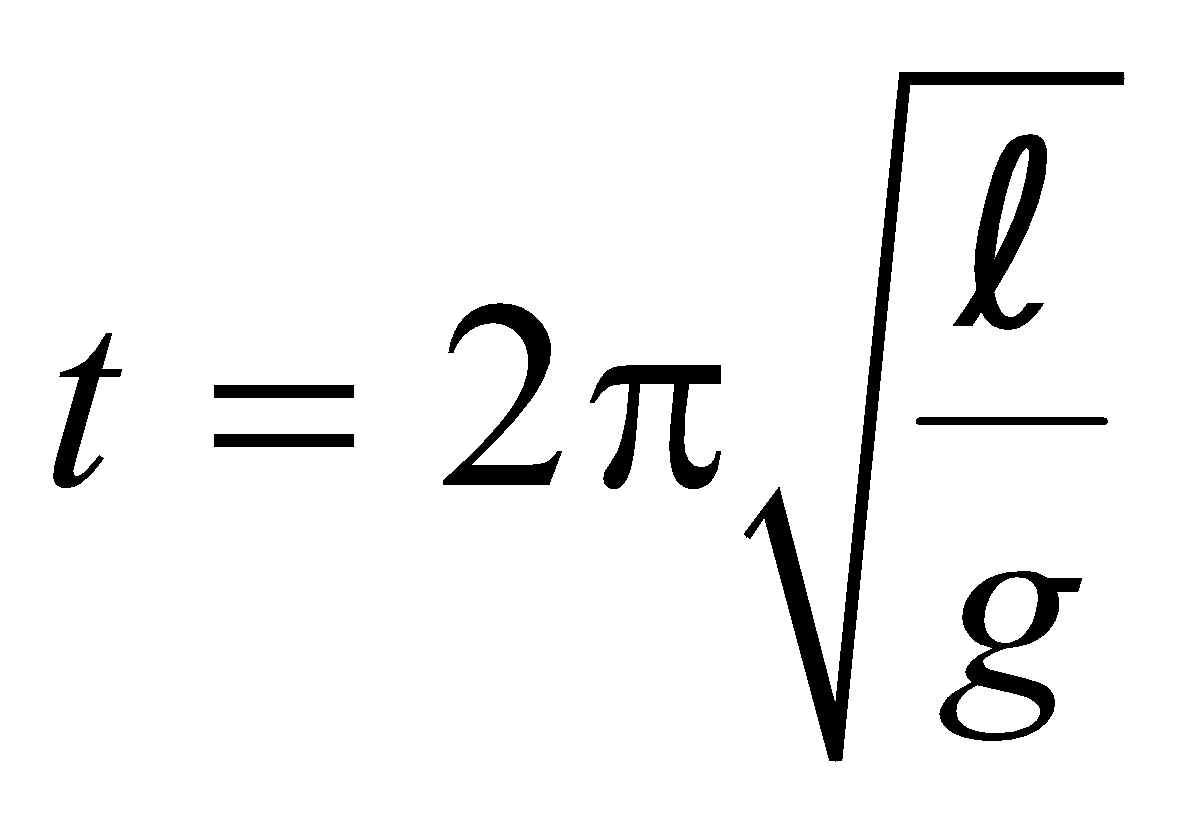
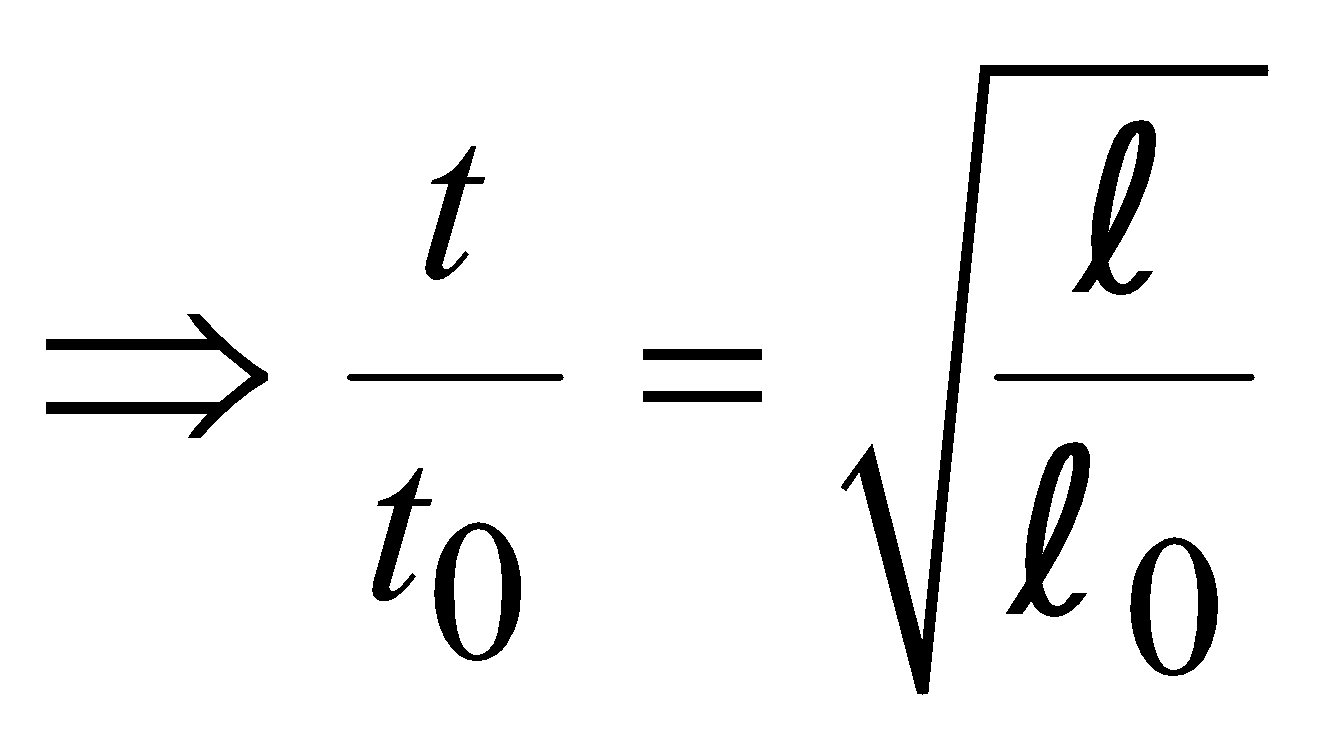 …..(i)
…..(i)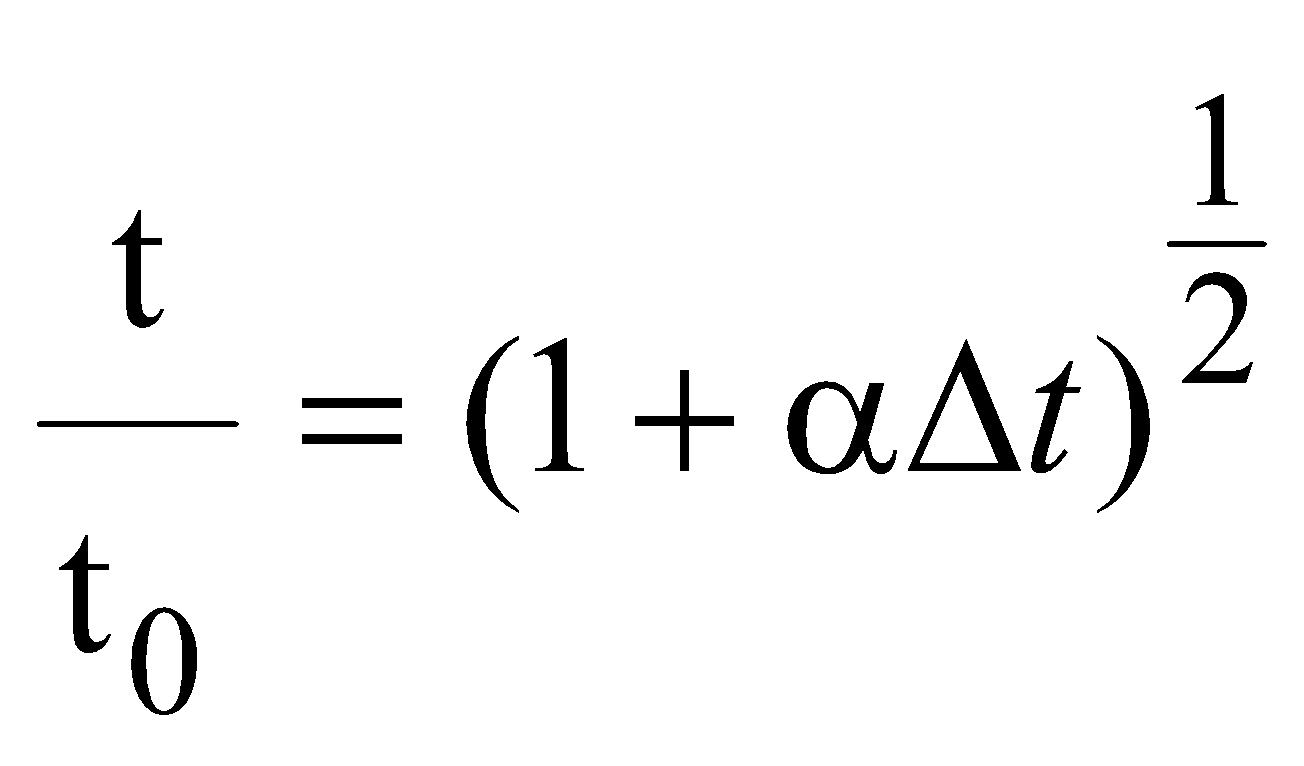
ERROR IN SCALE READING
ISOTHERMAL AND ADIABATIC ELASTICITIES
- Isothermal elasticity
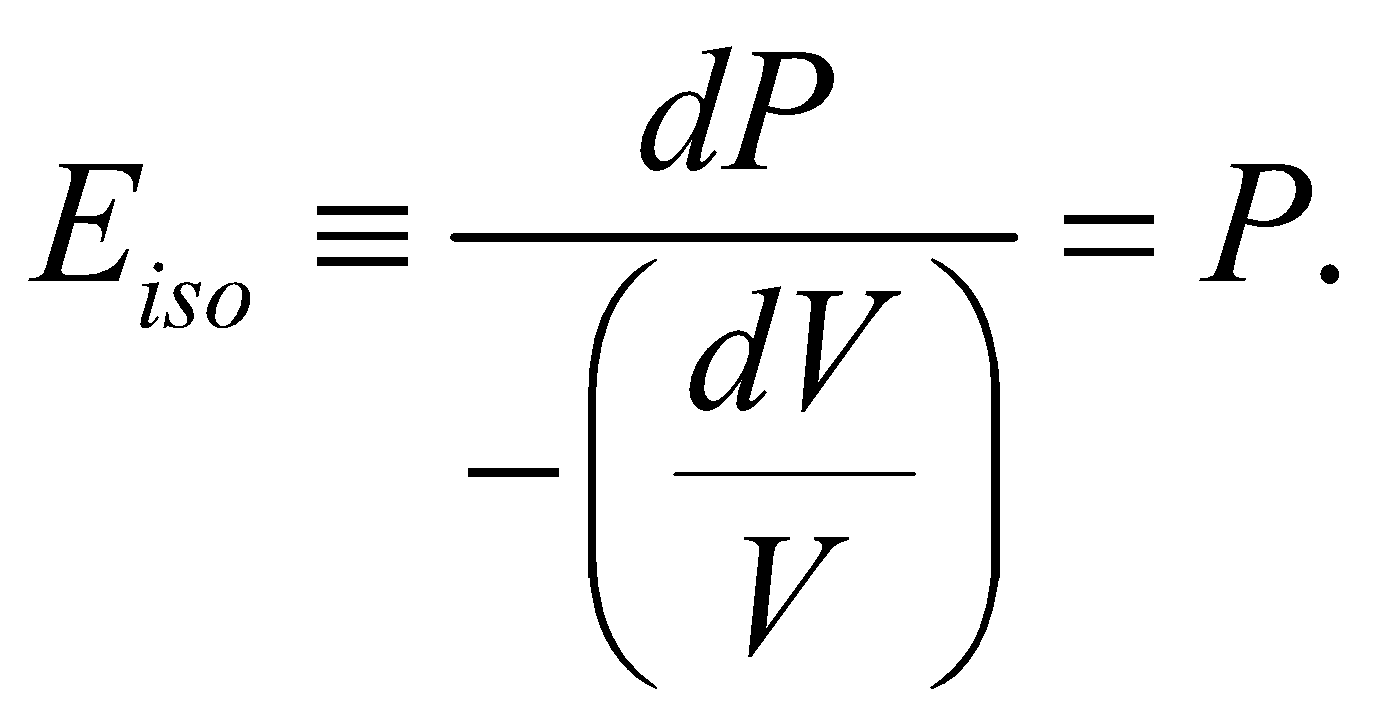 (since PV = RT = constant, )
(since PV = RT = constant, ) - Adiabatic elasticity
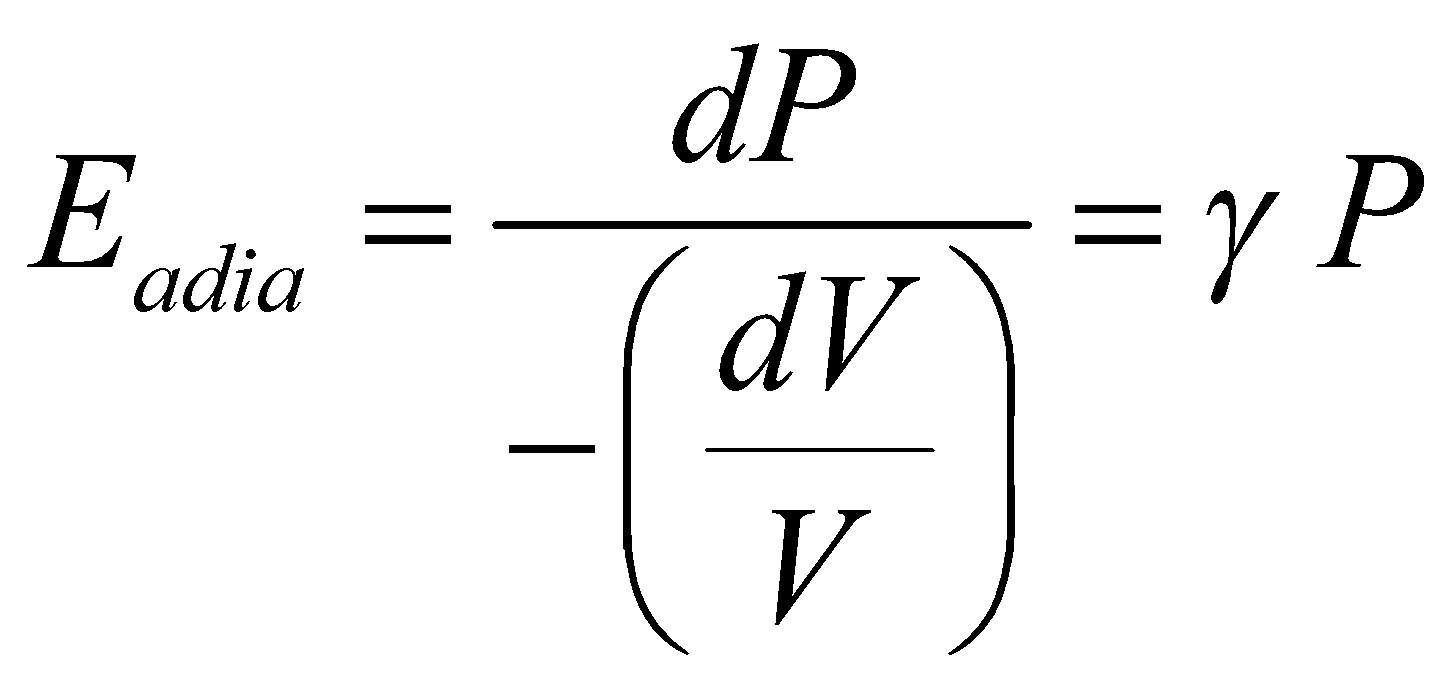 ; where
; whereEXPANSION OF GASES
- Pressure coefficient of expansion of gas (γP)
- Volume coefficient of expansion of gas (γv)
HEAT
- Calorie : It is the amount of heat required to raise the temperature of 1g of water from 14.5ºC to 15.5ºC.
- Kilocalorie, 1 Kcal = 1000 cal
- British Thermal Unit (BTU) : It is the fps unit of heat = 252 cal = amount of heat required to raise the temperature of 1 lb of water through 1ºF (from 63°F to 64ºF).
SPECIFIC HEAT CAPACITY
During the isothermal process Δt = 0 ⇒ c = ∞ (infinite)
- Molar specific heat at constant volume (CV) : It is the amount of heat required to raise the temperature of 1 mole of a gas through 1K or 1°C at constant volume.
- Molar specific heat at constant pressure (CP) : It is the amount of heat required to raise the temperature of 1 mole of a gas through 1K or 1°C at constant pressure.
CP – CV = R
THERMAL CAPACITY OR HEAT CAPACITY
WATER EQUIVALENT
PRINCIPLE OF HEAT (OR CALORIMETRY)
LATENT HEAT
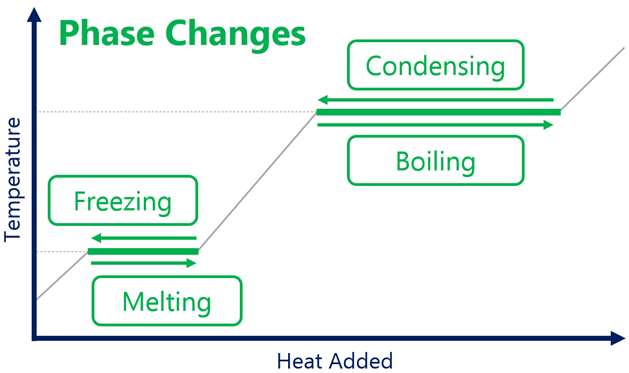
- Latent heat of fusion : It is the quantity of heat required to change unit mass of the solid into liquid at its melting point.
- Latent heat of vaporisation : It is the quantity of heat required to convert unit mass of liquid into vapour at its boiling point.
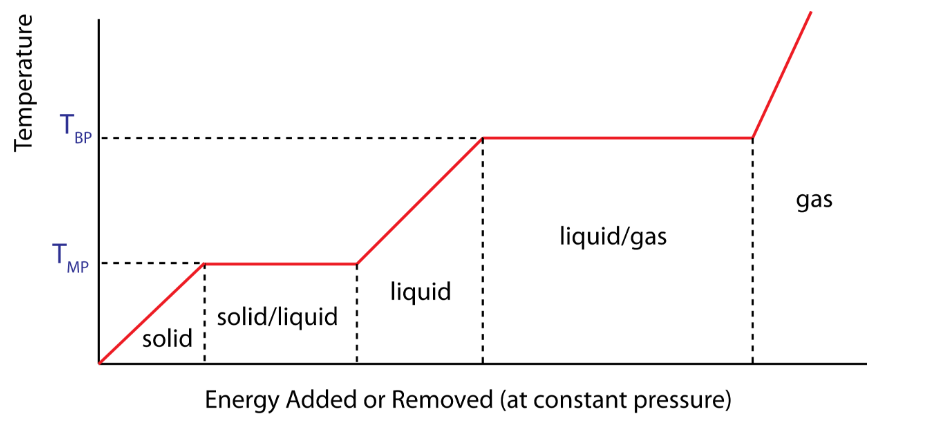
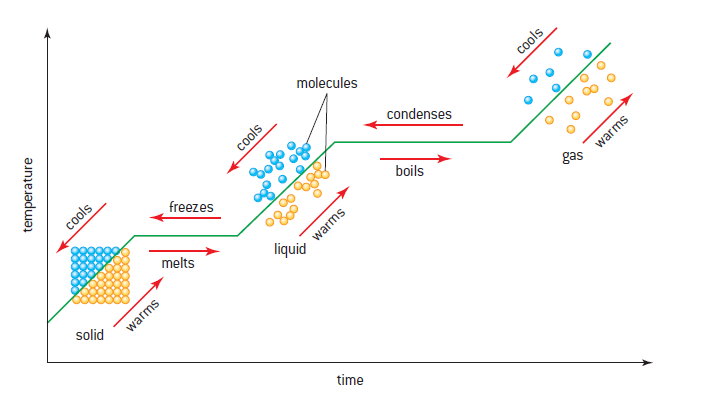
During this process of melting or vaporization, the temperature remains constant. The amount of heat needed to melt a solid of mass m may be written as
DIFFERENT PROCESSES OF PHASE CHANGE OR STATE CHANGE
- Sublimation : It is the process of conversion of solids to gaseous state on heating. On cooling the vapours get converted back into solids.
- Condensation : It is the process of conversion of gases/vapours to liquid state on cooling. On heating, these liquids are converted into vapours/gases.
- Boiling : It is the process of conversion of liquid to gaseous state on heating. It is a cooling process.
- Melting : It is the process in which solid gets converted into liquid on heating.
- Evaporation : Conversion of liquid into gaseous state at all temperatures is called evaporation. It is a phenomenon that occurs at the surface of the liquid.
- The heat capacity or thermal capacity depends on nature of the substance (specific heat capacity) and mass of quantity of matter of the body.
- In case of melting and boiling, the temperature does not change, only intermolecular potential energy of the system changes.
- System are in thermal equilibrium when their temperature are same or average kinetic energy per molecule is same.
- Internal energy is the sum of all energies in a system which includes energy of translational, rotational as well as vibrational motion of the molecules.
- The molar specific heat capacity depends on the molecular weight of the substance.
- The temperature, volume or pressure of a system may remain constant when it absorbs heat.
- When we press two block of ice together such that after releasing the pressure two block join this phenomenon is called regelation.
PHASE DIAGRAM
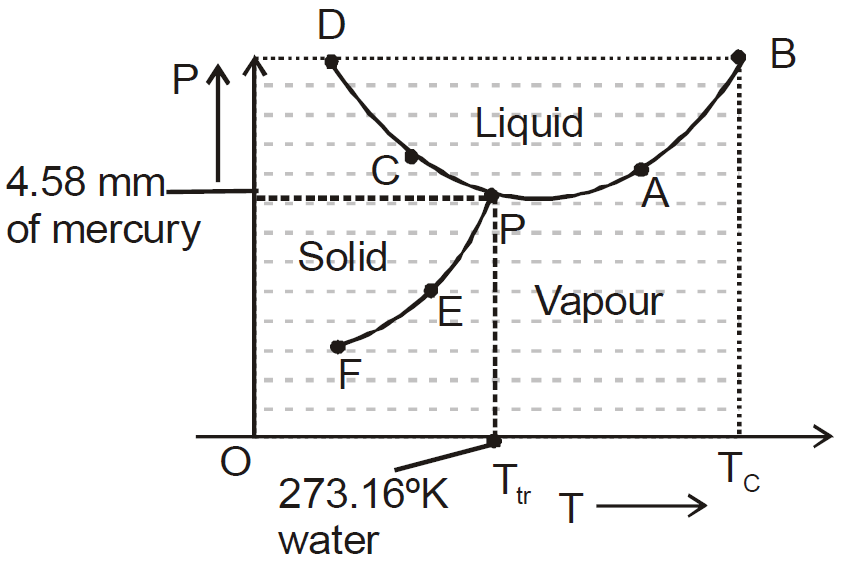
- The diagram shows vaporisation curve (AB), fusion curve (CD), sublimation curve (EF).
- For water, AB is called steam line, CD is called ice line and EF is called hoar-frost line.
- The temperature at which all the three states of matter (solid, liquid, gas) are mutually in thermal equilibrium is called the triple point (point P in diagram) of the substance.
- The temperature upto which a gas can be liquified under pressure alone is called the critical temperature (Tc).
SATURATED AND UNSATURATED AIR
VAPOUR PRESSURE
HUMIDITY
- Hygrometry is the branch of thermal physics that deals with the measurement of amount of water vapours present in the atmosphere.
- Hygrometer is an instrument used to determine dew point and relative humidity.
- Relative humidity is low when the air is dry.
- Saturated vapours do not obey (except Dalton’s law) gas laws, while unsaturated vapours obey them. The S.V.P. varies linearly with temperature (keeping volume constant) and equal to one atmospheric pressure at boiling point.(shown in fig.(a)) S.V.P. constant at constant temperature on increasing or decreasing volume fig. (b).
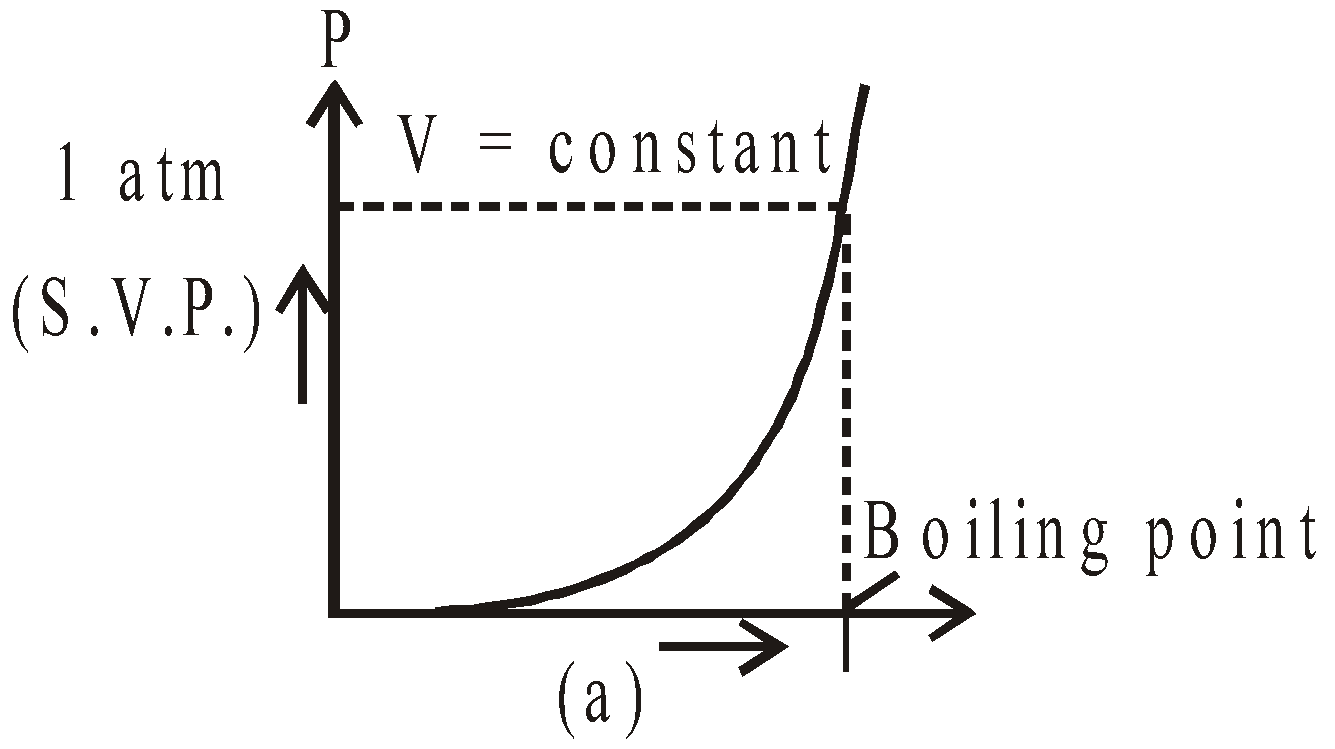

- At 0ºC, the saturation vapour pressure is 4.6 mm of Hg. Therefore, water vapours are always present around the ice. It increases with the increase in temperature.
- The relative humidity is 100% when the temperature of the atmosphere is equal to the dew point.
- Cryogenics is the study of low temperature.
- As RH is expressed in percentage, hence the maximum value of RH may be 100%.
- The saturation vapour pressure of water at 100ºC is 760 mm of Hg at sea level.
- As the temperature rises, the absolute humidity may increase and the relative humidity may remain constant or may even decrease.
- If the relative humidity is high then at the same temperature one feels hotter.
- If the air is absolutely dry, the dew point is not observed.
- The relative humidity decreases with the increase in temperature.
- If water is sprinkled in the room, both relative humidity as well as the dew point increase.
- Dew appears on the leaves of the trees etc. due to the condensation of saturated vapours.
- The mist or fog is the small droplets of water formed due to the condensation of water vapours near the surface of earth.
- Mist or fog formed much higher above the surface of earth is called cloud.
- The Relative humidity between 50% and 60% gives comfortable feeling to human beings.
- When the relative humidity is 100%, the reading of the dry and wet bulbs is same.
- Smaller the difference in the temperature of dry and wet bulbs, larger is the relative humidity.
- Water vapours are always seen around the ice, because the temperature around it is less than the dew point.
HEAT TRANSFER
- Conduction
- Convection
- Radiation
CONDUCTION
CONVECTION
RADIATION
- The equation
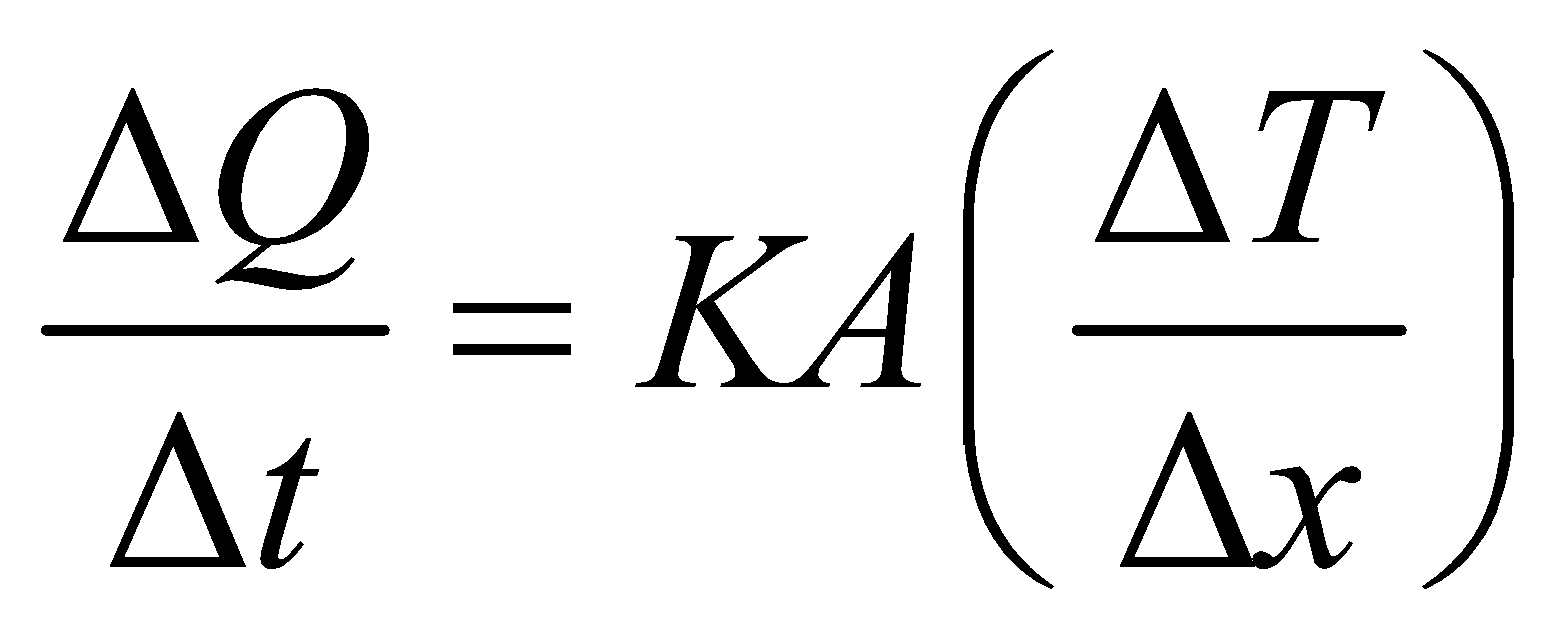 is valid for steady state condition. The condition is said to occur when no part of heat is used up in raising the temperature of any part of cross-section of the solid.
is valid for steady state condition. The condition is said to occur when no part of heat is used up in raising the temperature of any part of cross-section of the solid. - On comparing equation (1) with the following equation used for flowing of charge on account of potential difference.
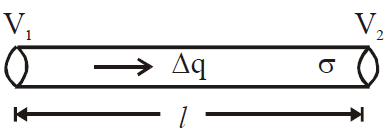
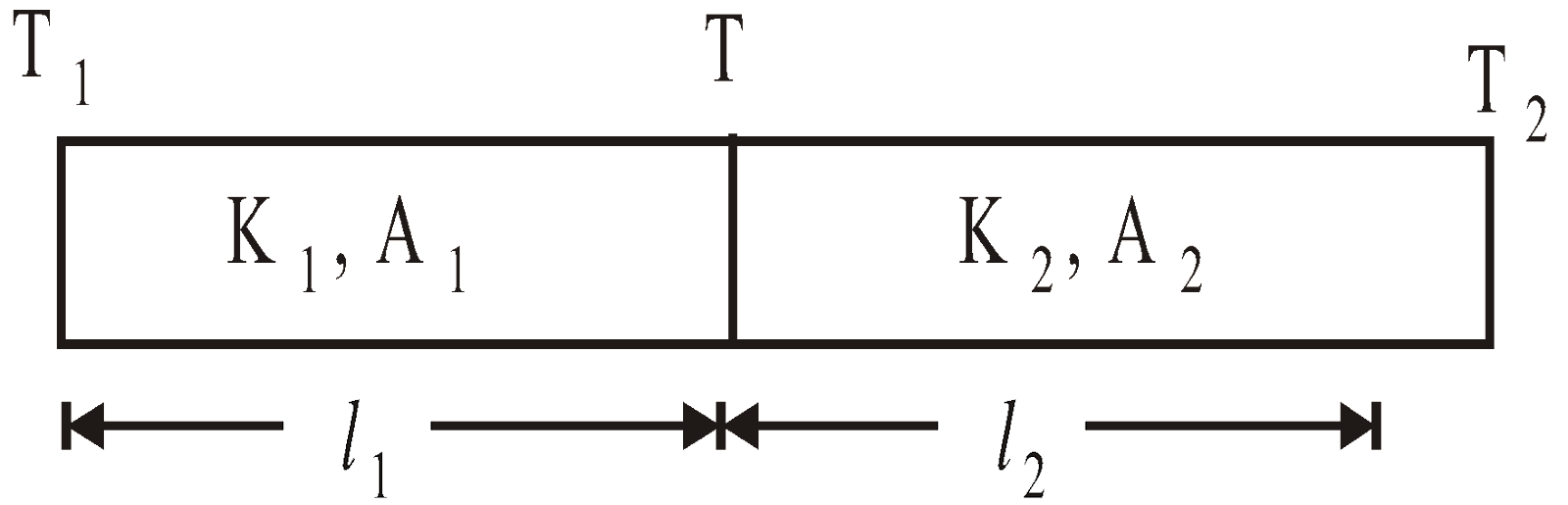
- Series combination of conductors

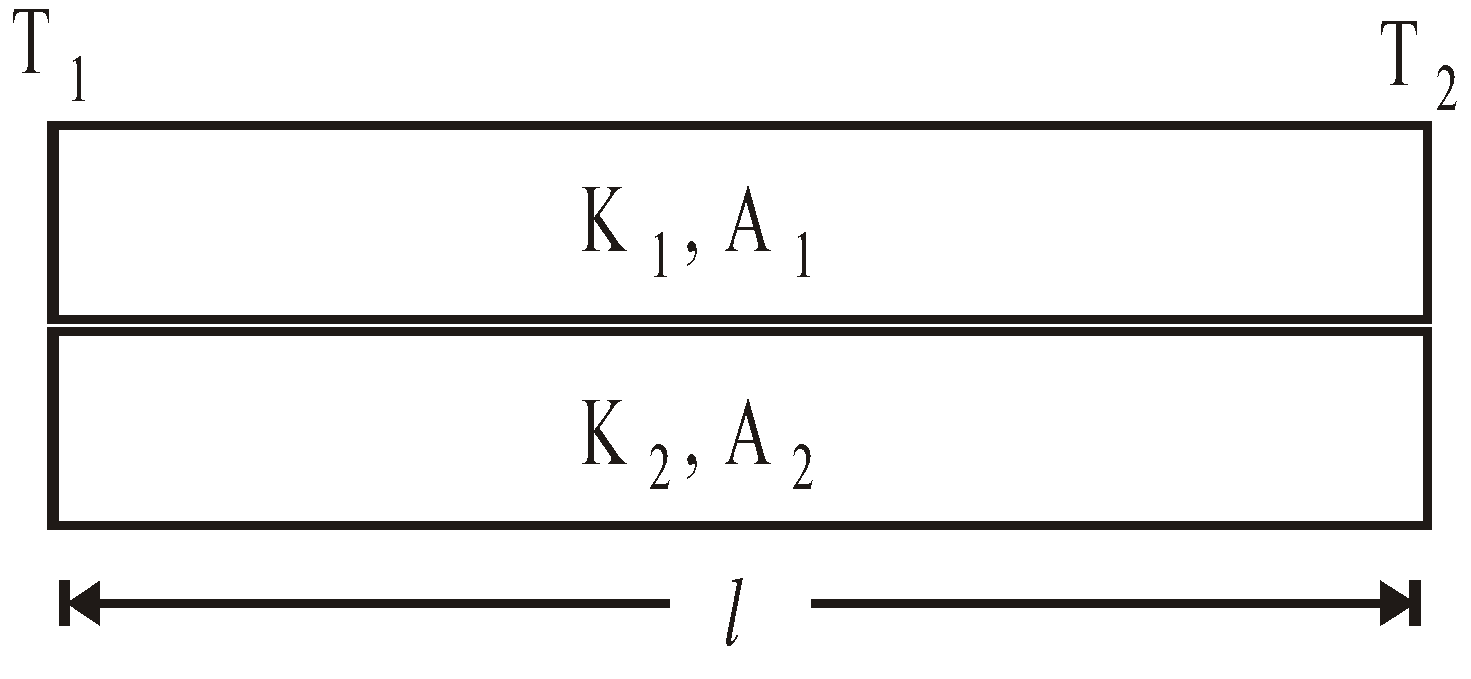
- Parallel combination of conductors
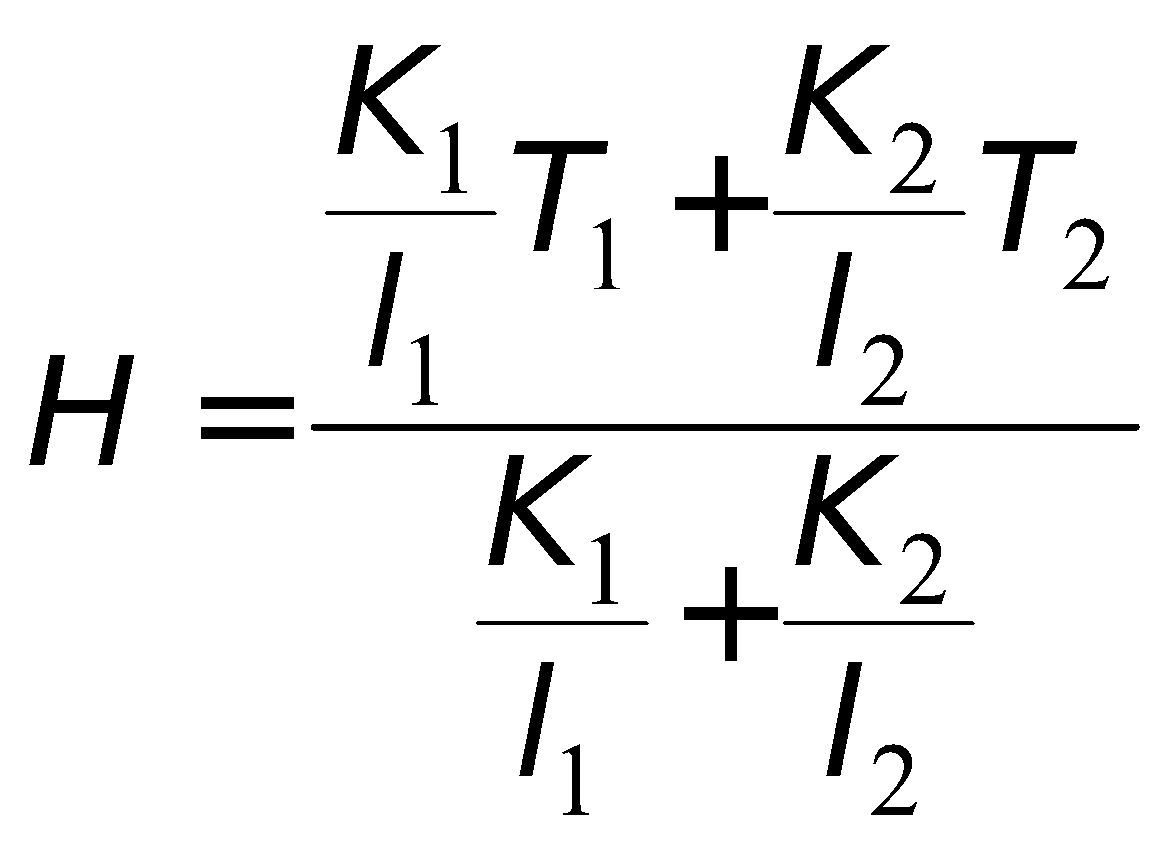
- Davy’s safety lamp is based on the conduction. It is used in mines to know the ignition temperature of gases. Danger of explosion can be avoided.
- Principle of chimney used in a kitchen or a factory is based on the convection.
- Land and sea breezes are due to the convection.
- Temperature of the upper part of the flame is more than the temperature on the sides, because the currents of air carry the heat upwards.
- Radiation can be detected by differential air thermometer, Bolometer, thermopile, etc.
HEAT TRANSFER BY RADIATION AND NEWTON’S LAW OF COOLING
STEFAN’S LAW
σ = 5.67×10–8 Wm–2 K–4.
WIEN’S LAW
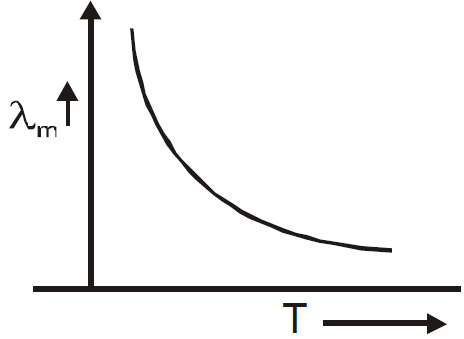
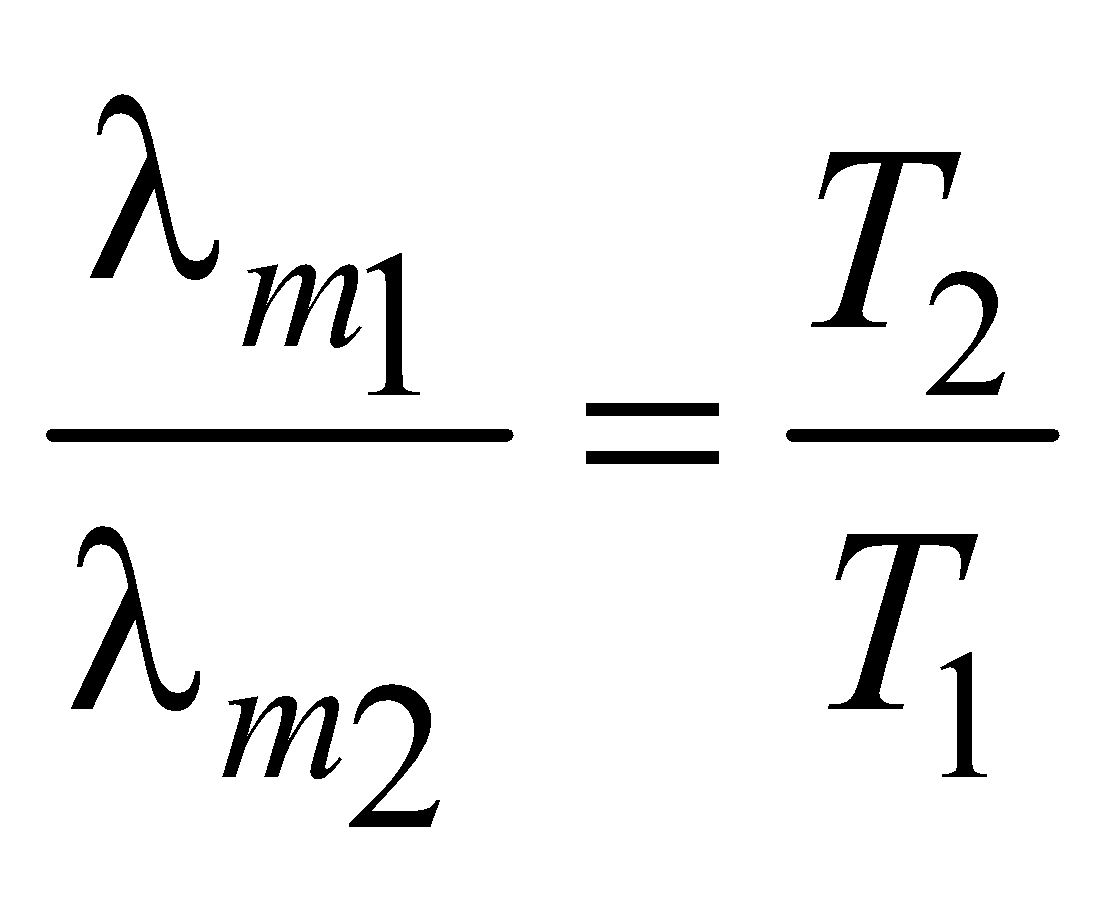
KIRCHOFF’S LAW
- For a perfect black body, A = 1,
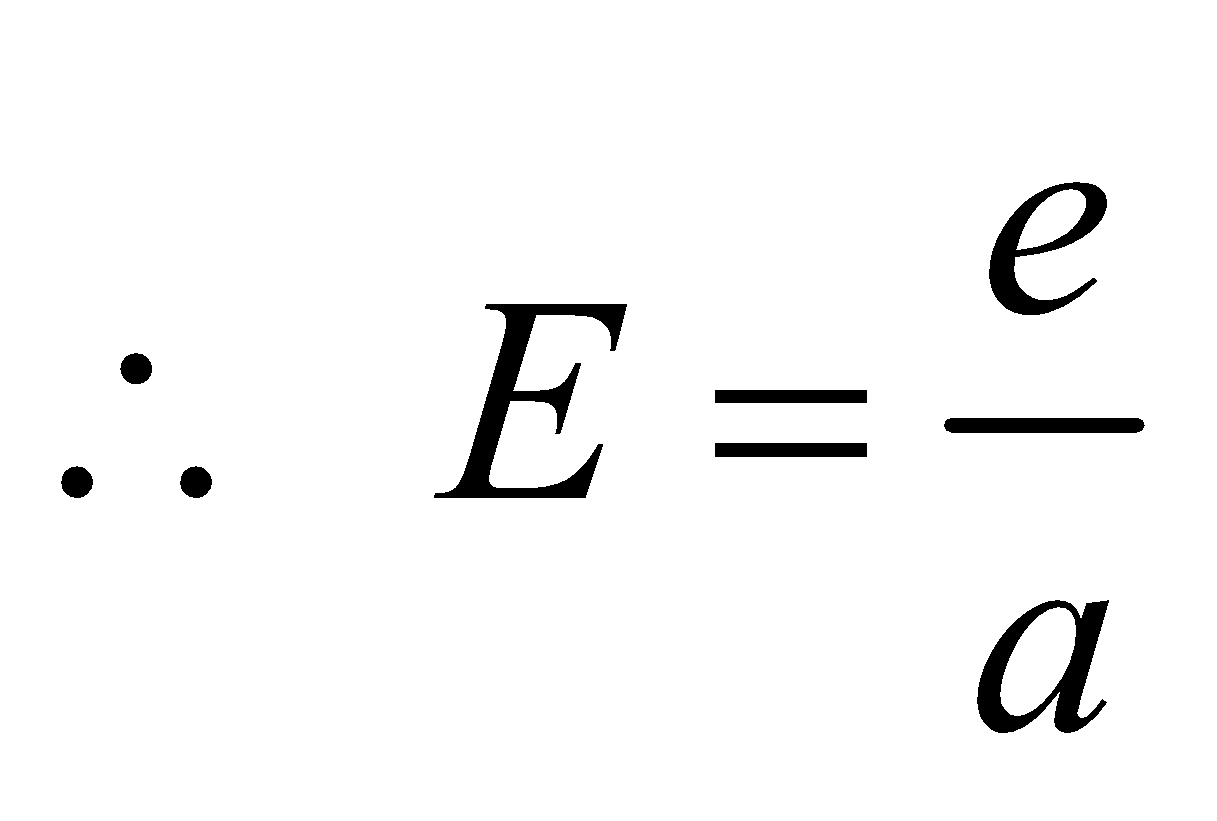
- If emissive and absorptive power are considered for a particular wavelength λ then
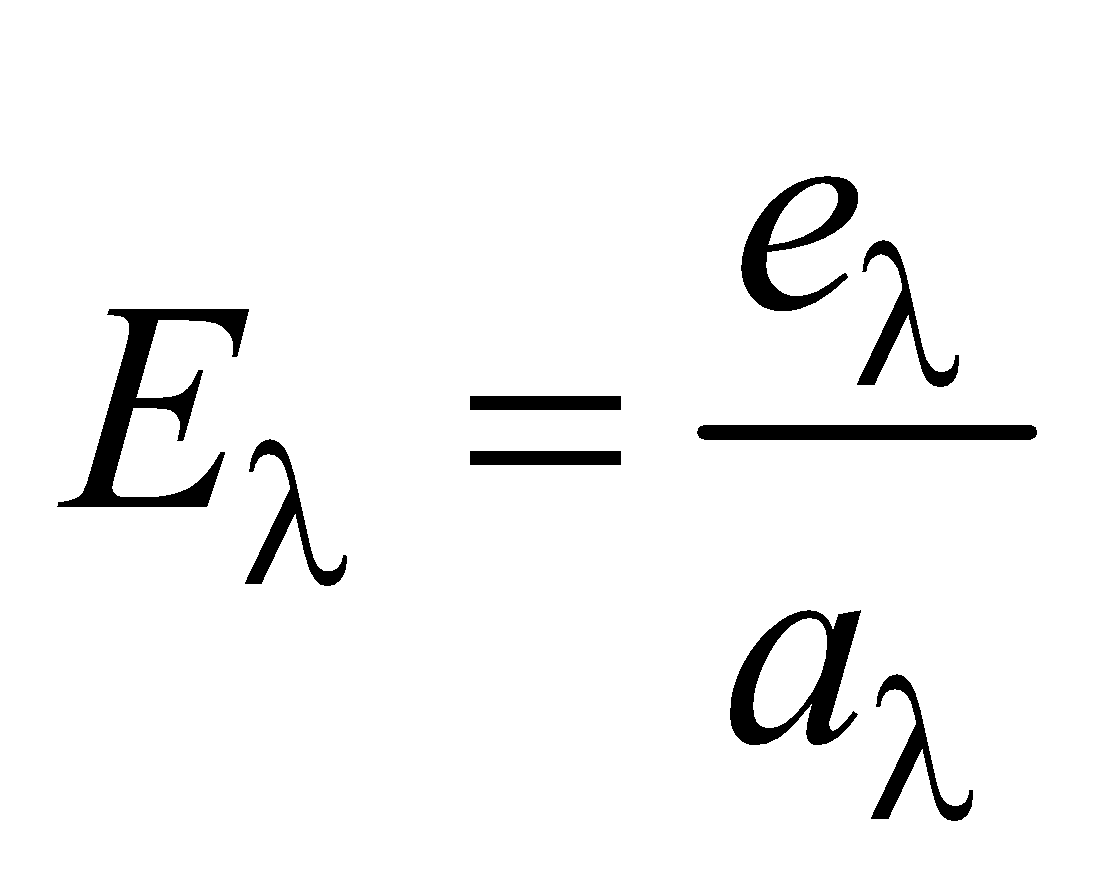
- Since Eλ is constant at a given temperature, according to this law if a surface is good absorber of a particular wavelength then it is also a good emitter of that wavelength.
FRAUNHOFER’S LINE
- Fraunhofer lines are the dark lines in the spectrum of sun and are explained on the basis of Kirchoff’s law. When white light emitted from central core of sun (photosphere) passes through its atmosphere (chromosphere) radiation of those wavelength will be absorbed by the gases present there, which they usually emit (as good emitter is a good absorber) resulting dark lines in the spectrum of sun.
- On the basis of Kirchoff’s law, Fraunhofer identified some of the elements present in the chromosphere. They are hydrogen, helium, sodium, iron, calcium, etc. Fraunhofer had observed about 600 darklines in the spectrum of sun.
NEWTON’S LAW OF COOLING
SOLAR CONSTANT
- Good absorber is a good emitter.
- Cooking utensils are provided with wooden or ebonite handles, since wood or ebonite is a bad conductor of heat.
- Good conductor of heat are good conductors of electricity, Mica is an exception which being a good conductor of heat is a bad conductor of electricity.
