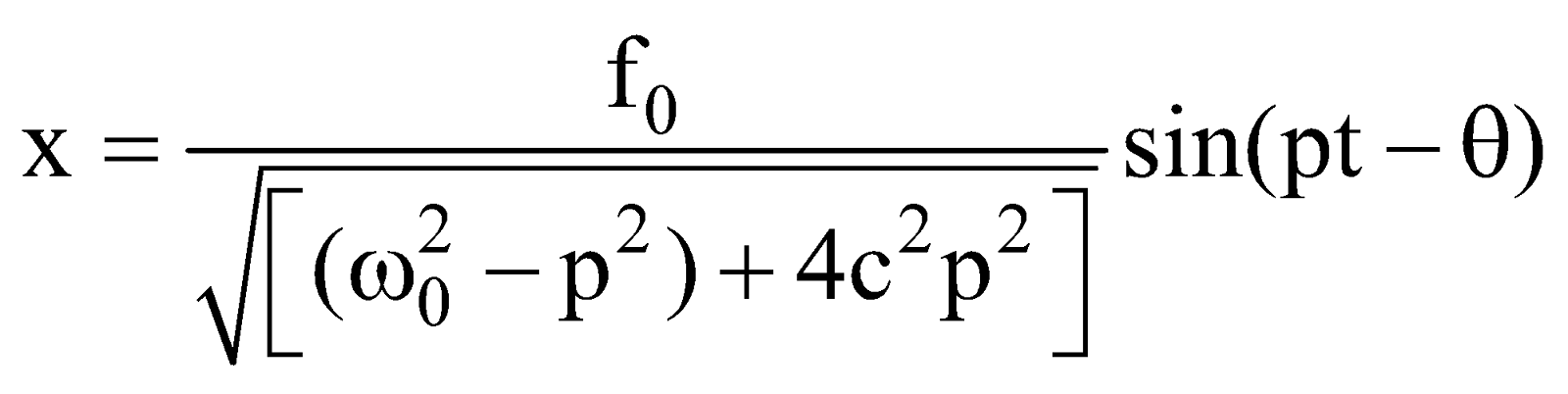4.1 Oscillations
Essential Idea:
A study of oscillations underpins many areas of physics with simple harmonic motion (shm), a fundamental oscillation that appears in various
natural phenomena.
Understandings:
- Simple harmonic oscillations
- Time period, frequency, amplitude, displacement and phase difference
- Conditions for simple harmonic motion
Applications and Skills:
- Qualitatively describing the energy changes taking place during one cycle of an oscillation
- Sketching and interpreting graphs of simple harmonic motion examples
Data booklet reference:
- a ∝ -x
- \(T=\frac{1}{f}\)
Big Ideas
- • Simple harmonic motion is a repeating relationship between an object’s position, velocity, and acceleration
- • Waves are formed and transferred by particles oscillating in a medium
- • All waves have properties can be measured and mathematically related
- • Instruments resonate at specific frequencies due to the number of standing waves that fit in the length of the system
- • Waves can occupy the same space at the same space to create constructive or destructive interference
Content Objectives
Simple Harmonic Motion
- I can qualitatively describe the motion of an oscillating system
- I can relate the acceleration of an object in simple harmonic motion to its position
- I can graph the displacement, velocity, and acceleration vs time for simple harmonic motion
- I can interpret an SHM graph to describe the conditions at a specific point in an object’s motion
- I can describe and relate the properties of period and frequency
- I can calculate period and frequency from a scenario
- I can qualitatively describe the energy changes that take place during an oscillation
Properties of Traveling Waves
- I can describe how waves carry energy through a medium
- I can compare the properties of transverse and longitudinal waves
- I can identify a wave example as transverse or longitudinal
- I can read a wave’s amplitude, wavelength, period, and frequency from a graph
- I can label a graph with the location of a wave’s crest/compression and trough/rarefaction
- I can describe the number of complete wavelengths represented in a picture
- I can use the wave speed equation to mathematically relate speed, wavelength, and frequency
- I can relate pitch and frequency for sound waves
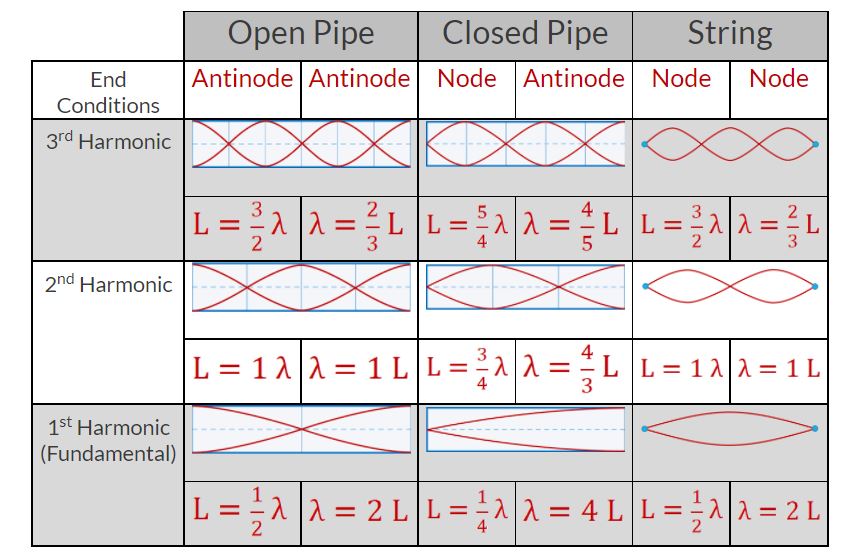
Standing Waves and Sound
- I can describe the motion of a standing wave
- I can identify and label the node and antinodes on a standing wave diagram
- I can calculate the wavelength of a standing wave for different harmonics
- I can describe how harmonics make it possible for one system to resonate at different frequencies
- I can describe the end conditions and nodes/antinodes for open/closed pipes and vibrating strings
- I can relate length and wavelength for open/closed pipes and vibrating strings
- I can calculate the length of a pipe/string required to resonate a specific frequency
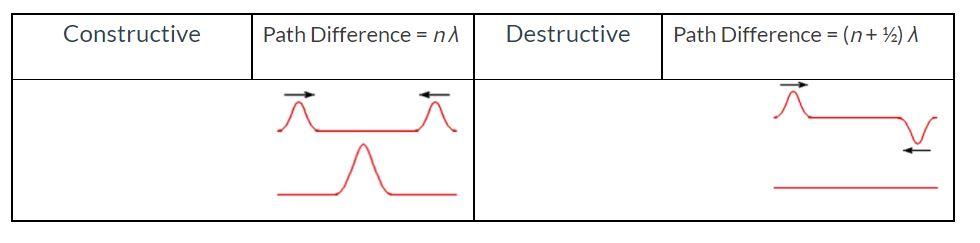
Speed of Sound and Wave Interference
- I can describe why sound travels at different speeds in different media
- I can calculate how far a distant object is by timing an echo
- I can qualitatively and quantitatively interpret cases of constructive and destructive interference
- I can add up two waves with superposition to create a new waveform
- I can describe applications and real-world examples for wave interference
- I can use wavelength and source distance to identify maxima and minima for interference
Waves – Sound
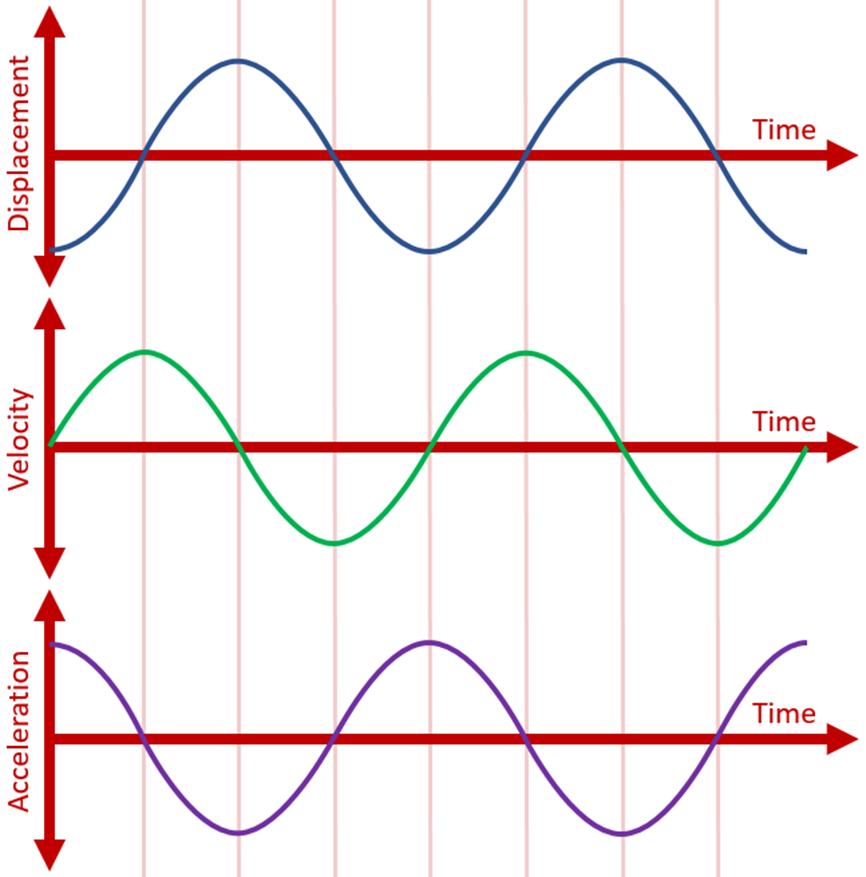
Simple Harmonic Motion Graphs
 | Velocity vs Displacement
| Accel. vs Displacement
|
Parts of a Wave
Label the Wave:
|  |
Harmonics
Interference
OSCILLATIONS
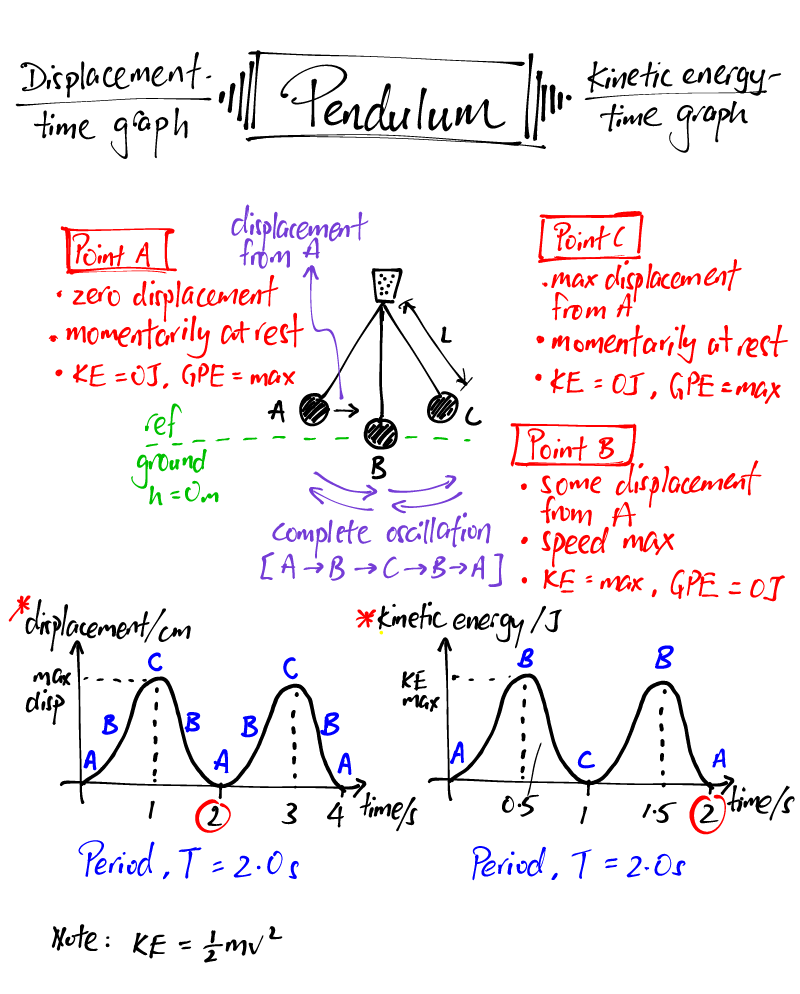
PERIODIC AND OSCILLATORY MOTION
PERIODIC MOTION
- Motion of moon around earth
- Motion of a piston in a cylinder
- Motion of a simple pendulum etc.
OSCILLATORY MOTION
- The motion of a ball in bowl

- The needle of a sewing machine
- Vibrations of prongs of tuning fork etc.
- All oscillatory motion are periodic but all periodic motion are not oscillatory motion.
- The oscillatory motion which can be expressed in terms of sine and cosine function, is said to be harmonic motion.
SIMPLE HARMONIC MOTION (S.H.M.)
- Motion of a body suspended by a spring
- Oscillations of simple pendulum
EQUATIONS OF S.H.M.
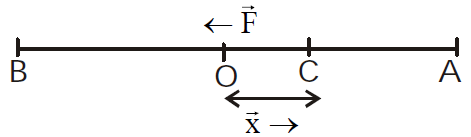
TERMS RELATED TO S.H.M.
- Amplitude : The maximum displacement of the oscillating particle on either side of its mean position is called its amplitude. It is denoted by A.
- Time period : The time taken by a oscillating particle to complete one oscillation is called its time period. It is denoted by T.
- Frequency : It is the number of oscillations completed in one second.
It is denoted by υ.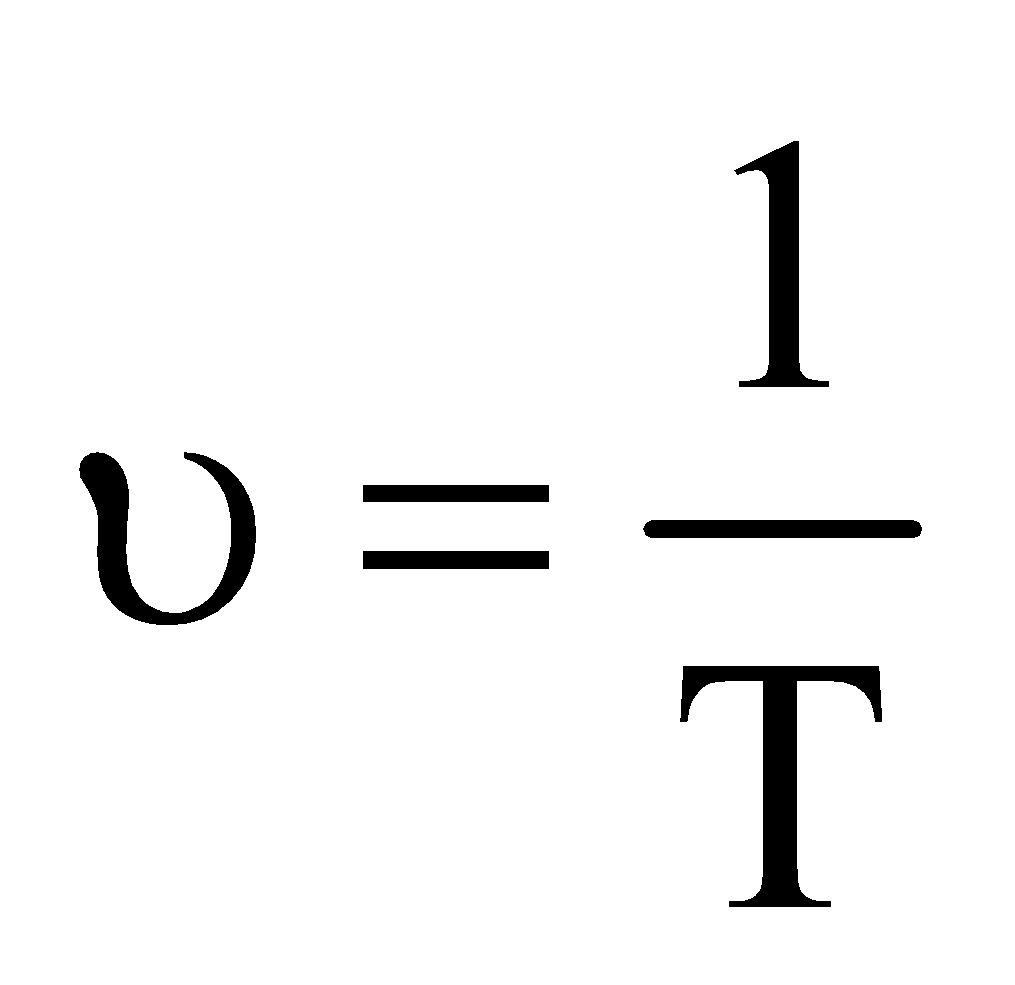
- Angular frequency
- Phase : The parameter, by which the position of particle from its mean position is represented, is known as phase. The phase at any instant tells the state of position & direction of motion at that instant. The phase at time t = 0 is known as the initial phase or epoch (e).
- Total phase angle : The total angle (ωt + θ) is known as total phase angle.
CHARACTERISTICS OF S.H.M.
The displacement of a particle in S.H.M. is given by
The velocity of a particle in S.H.M. is given by

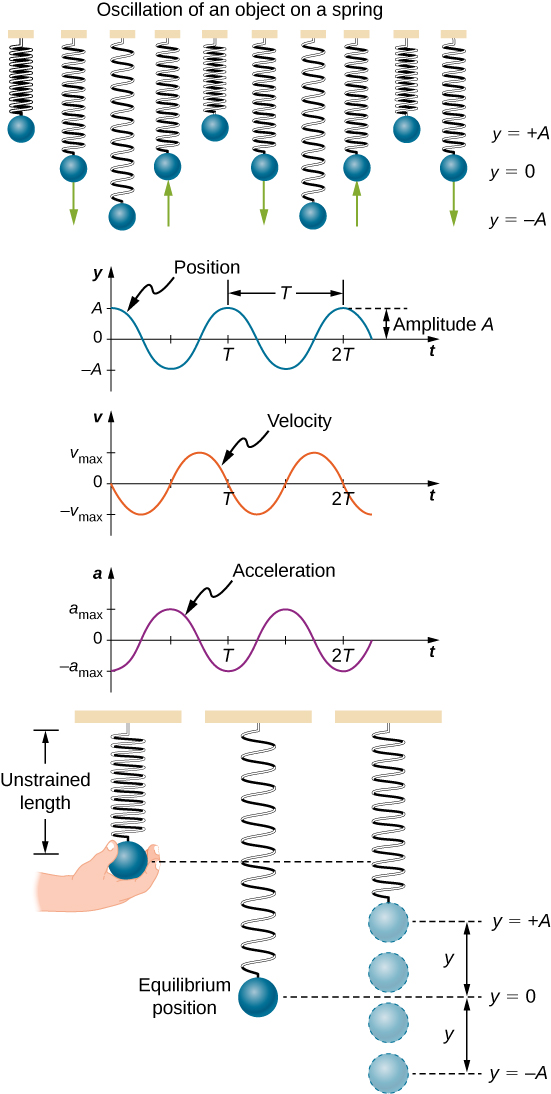

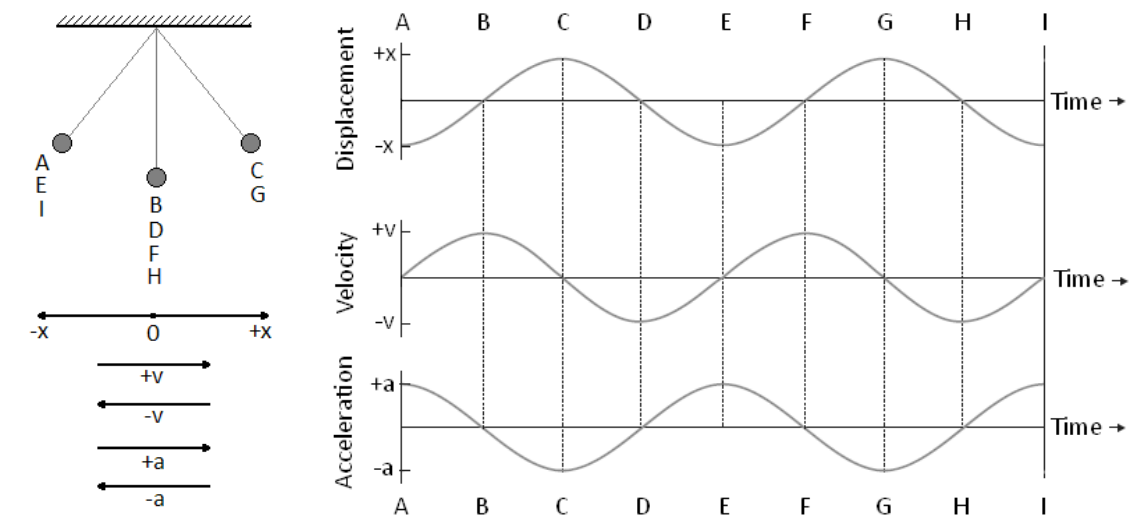
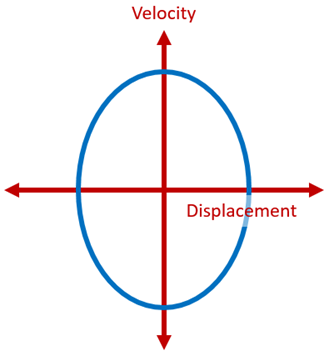
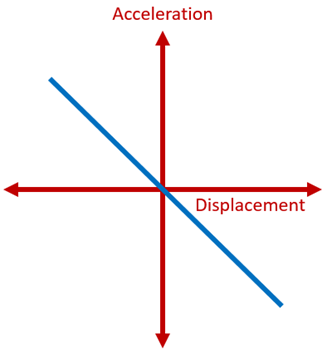
Graphical Representation of Simple Harmonic Motion
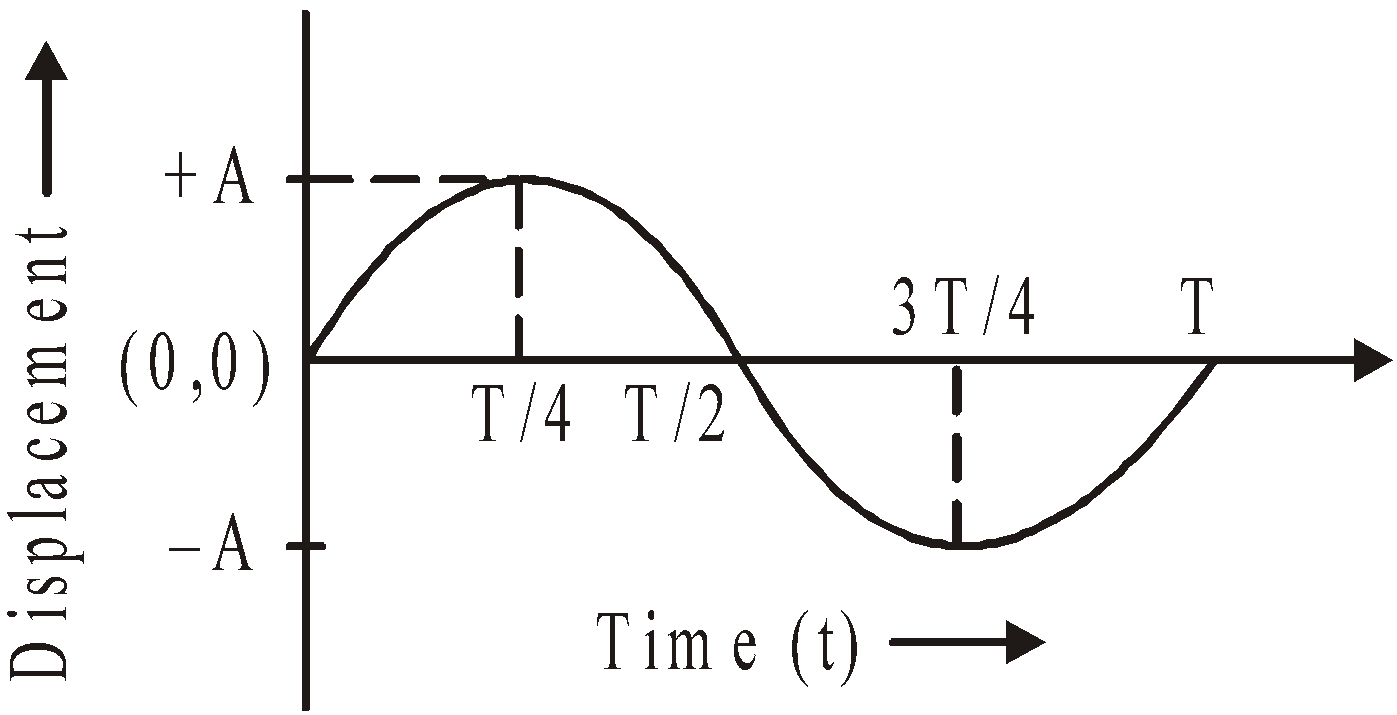
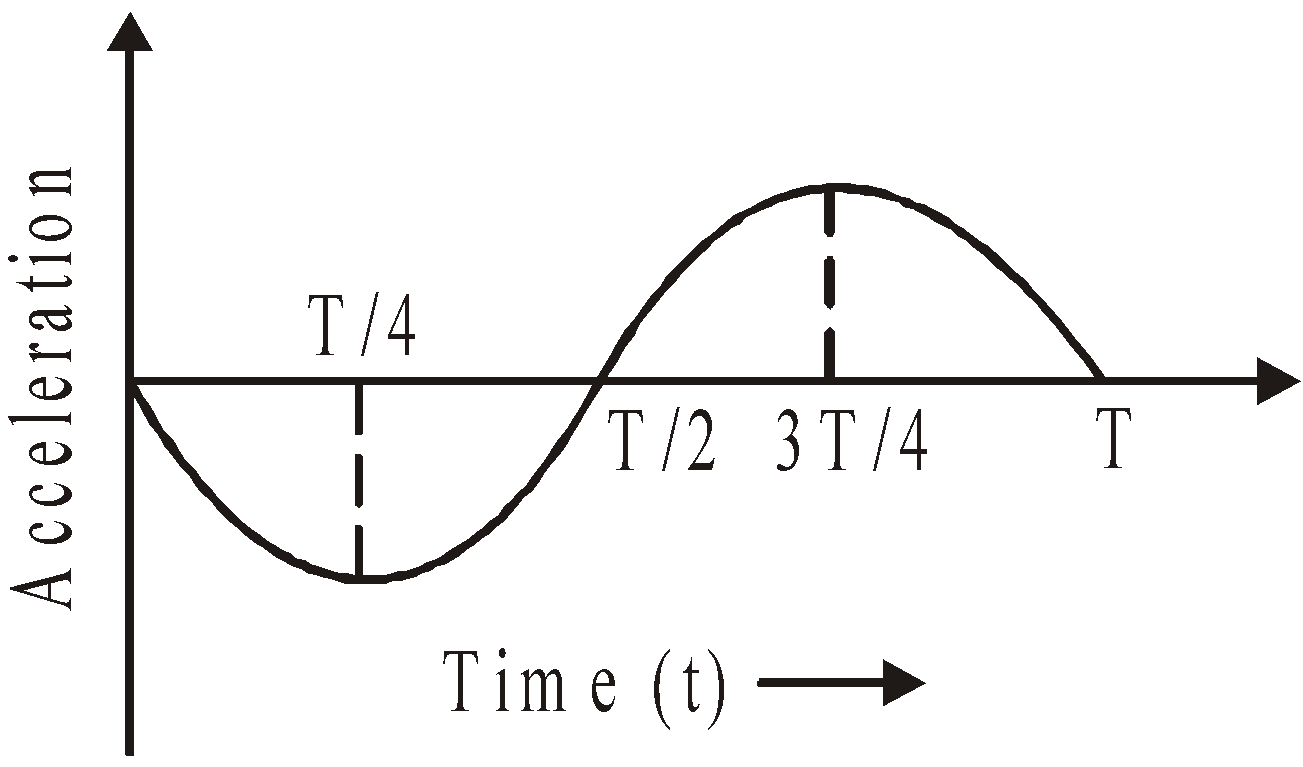
The graphical representation of displacement, velocity and acceleration of the particle vibrating in SHM is given below.
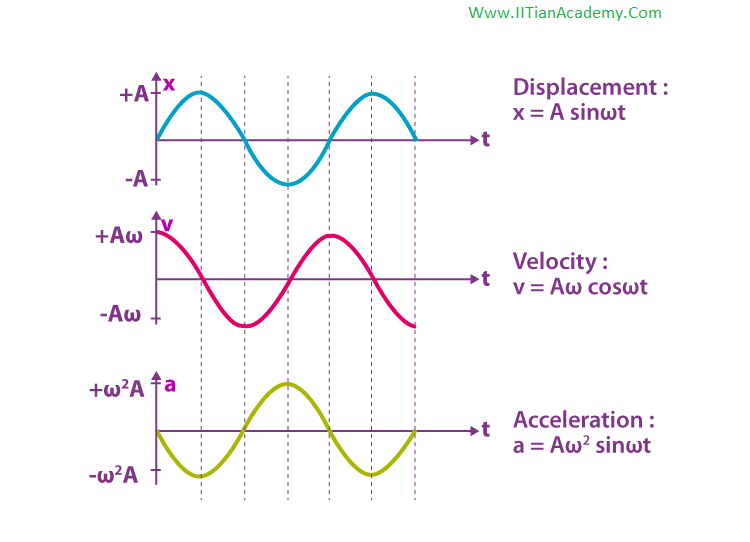
(i) The displacement of the particle is given by the expression y = A sin ωt. When y = ± A, the displacement of the particle is maximum.
The equation of velocity can also be written as y = A sin (ωt + 0) ——-(1)
(ii) The velocity of the particle executing SHM is given by v = Aω cos (ωt). The velocity of the particle is maximum at the mean position i.e., v = ± Aω and at the extreme position, it will be zero.
The equation of velocity can also be written as v =Aω sin (ωt + π/2) ——–(2)
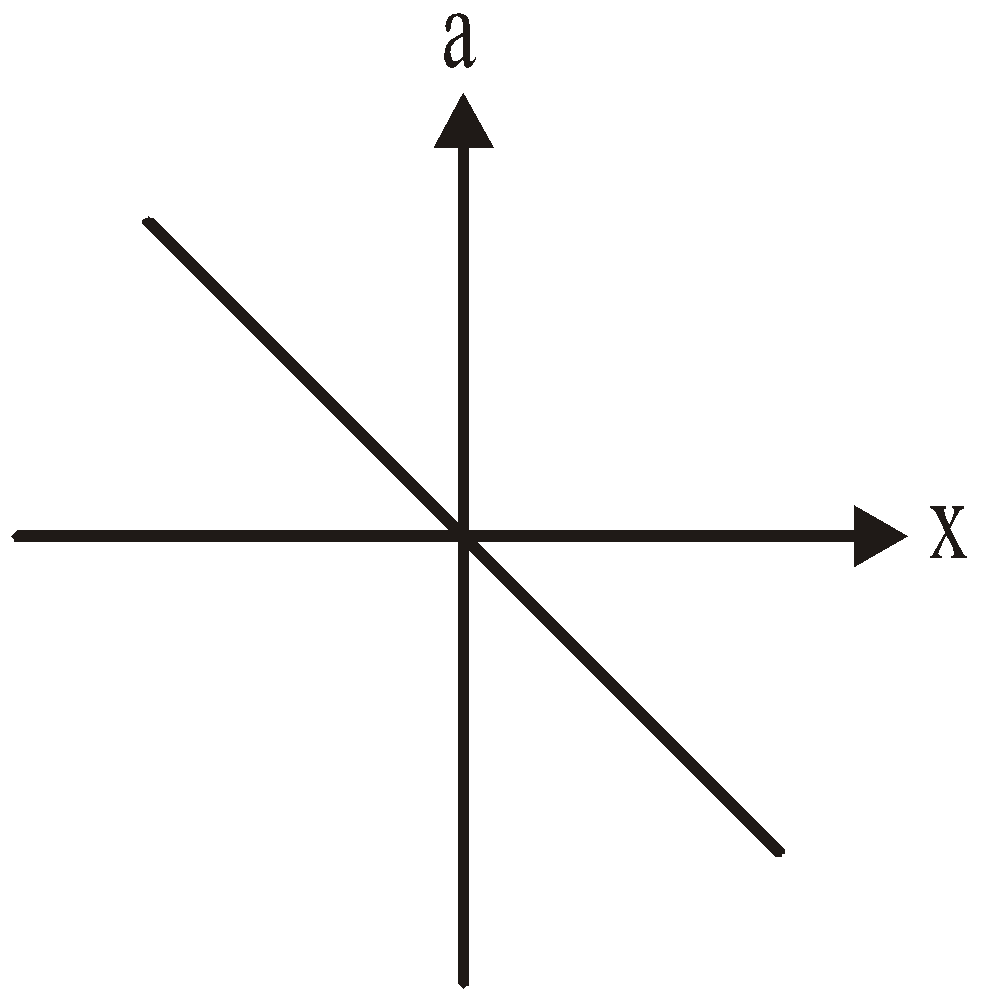
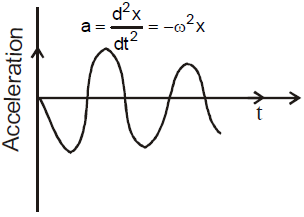
(iii) The acceleration of the particle executing simple harmonic motion is a = – Aω2sin(ωt). The acceleration will be maximum at the extreme position and it is zero at the mean position.
The equation of acceleration can also be written as a = Aω2 sin (ωt + π) ——–(3)
From the equations (1), (2) and (3) we can understand that the phase difference between displacement – velocity is π/2 , Velocity – acceleration is π/2. and between displacement and acceleration is π.
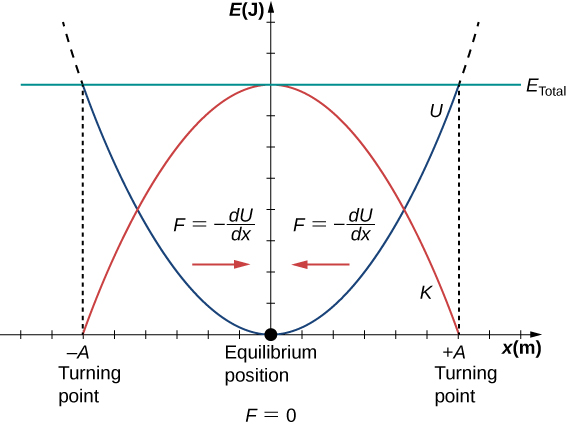
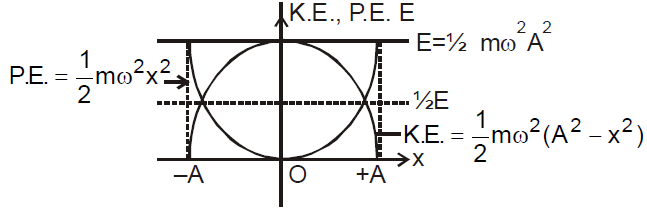
- Kinetic energy : A particle in S.H.M. possesses kinetic energy by virtue of its motion.
- Potential energy : A particle in S.H.M. possesses potential energy due to its displacement from the mean position.
- Total mechanical energy
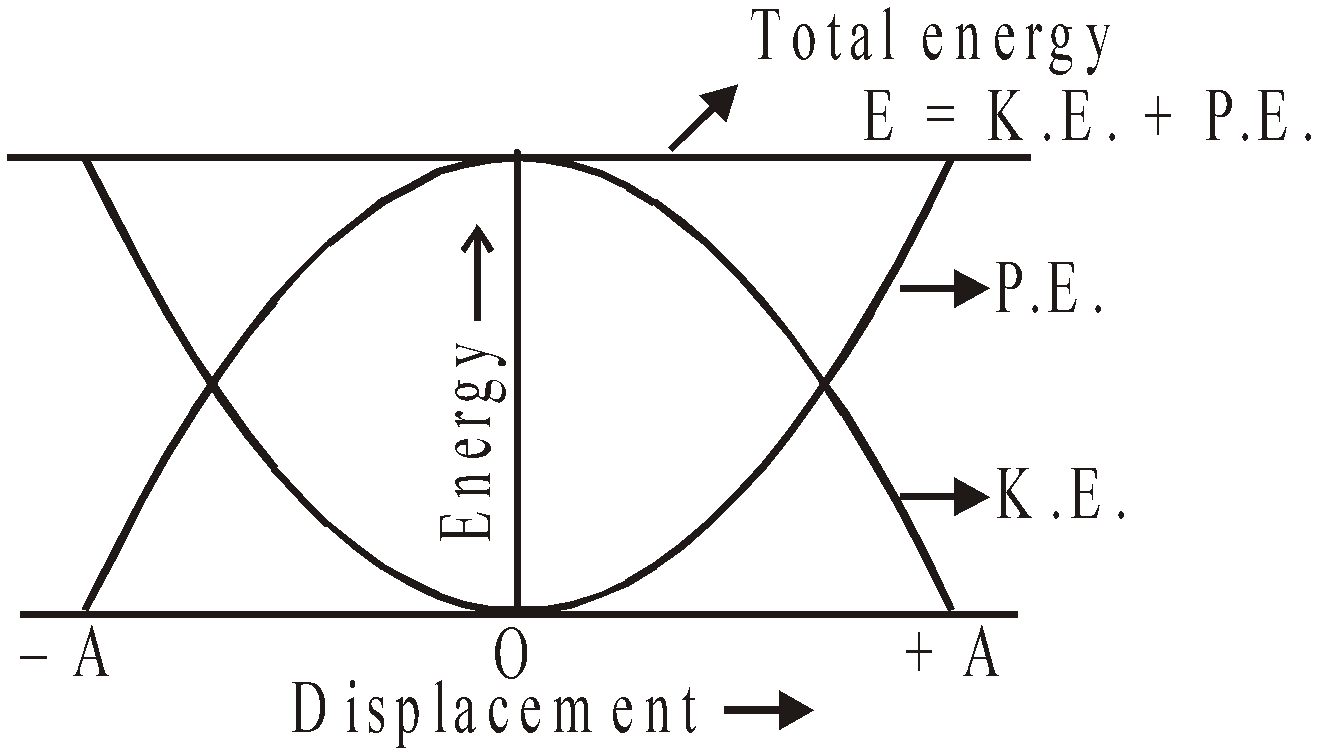
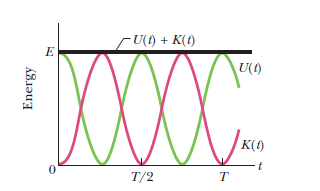
As time changes, the energy shifts between the two types, but the total is constant.
- Restoring force F = – Mω2x
- Kinetic energy = (1/2) Mω2(A2 – x2)
- Potential energy = 1/2 Mω2x2
- Total energy of SHM = 1/2 Mω2A2
- The kinetic and potential energy of SHM varies sinusoidally with a frequency twice that of SHM.
- Total energy \(\frac{1}{2}m\omega^2 A^2 = 2\pi^2 m A^2 n^2\)
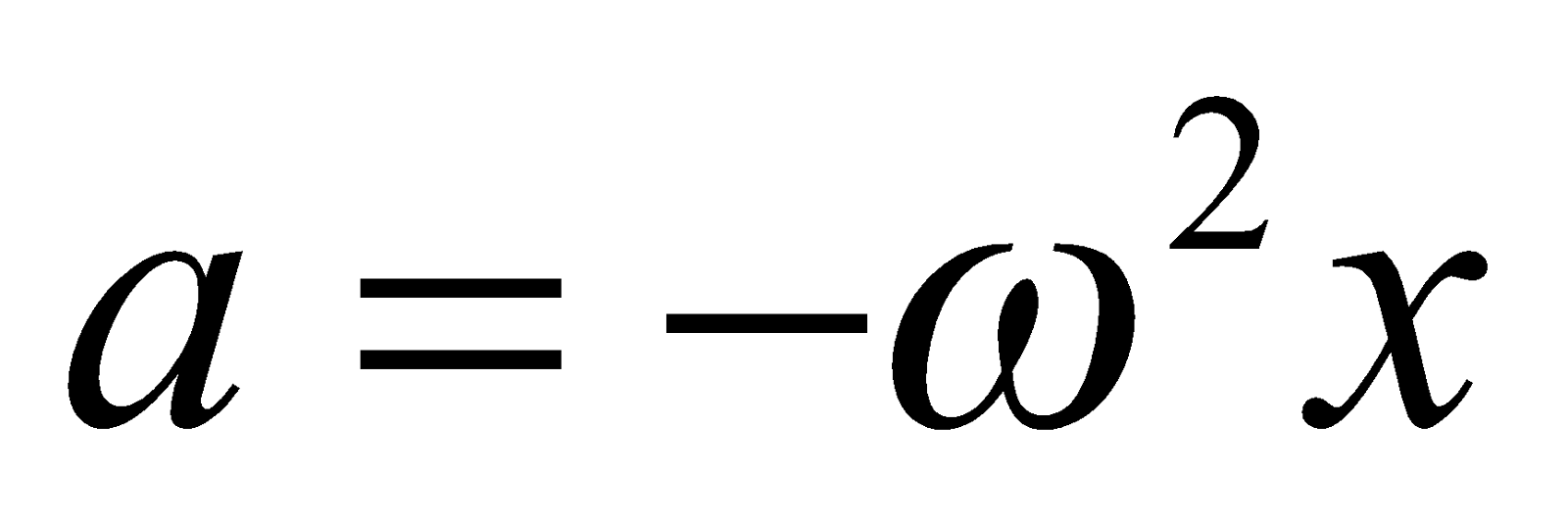 where ω is constant
where ω is constant 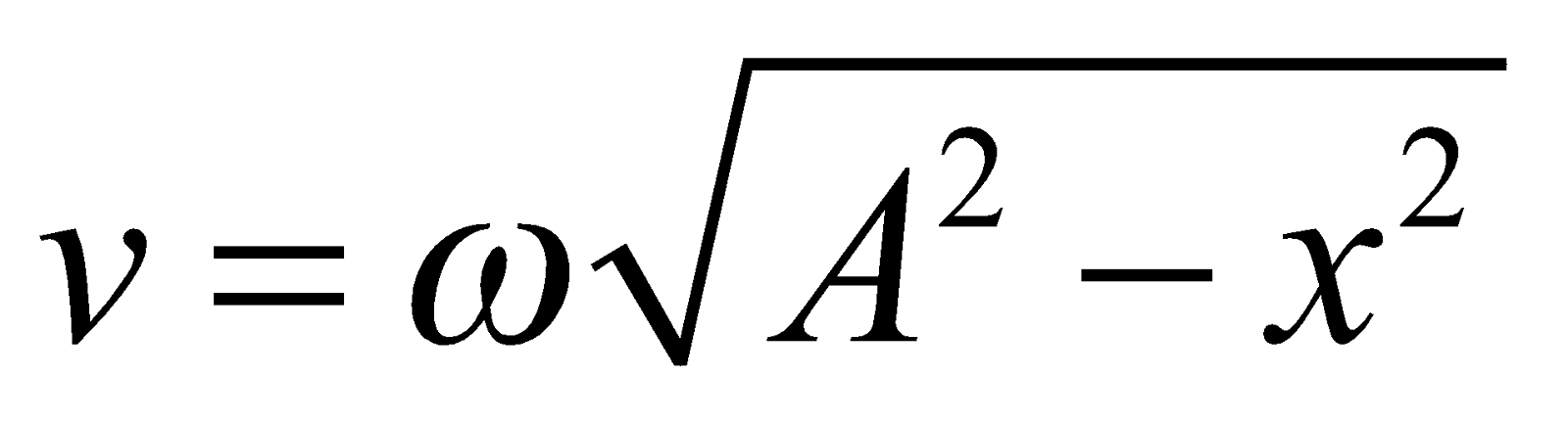
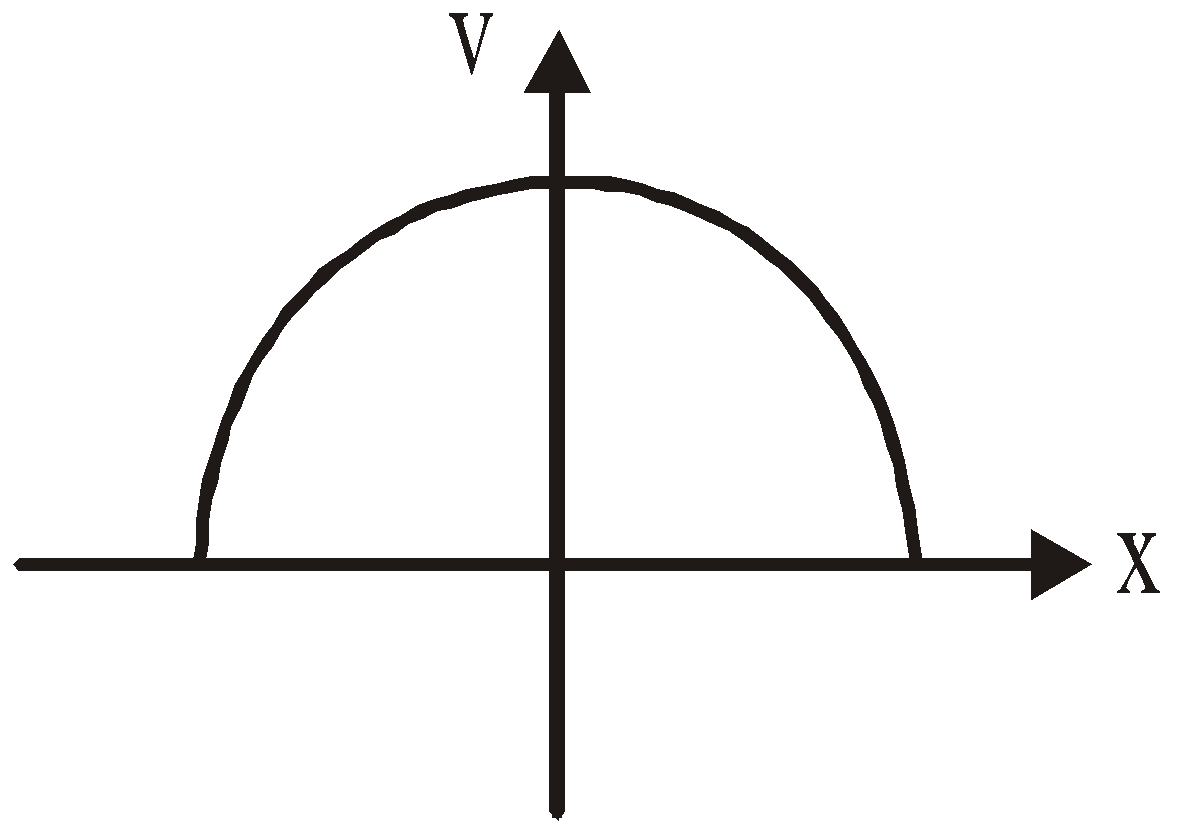
- Geometrically the projection of the body undergoing uniform circular motion on the diameter of the circle is SHM.
- In a non-inertial frame.
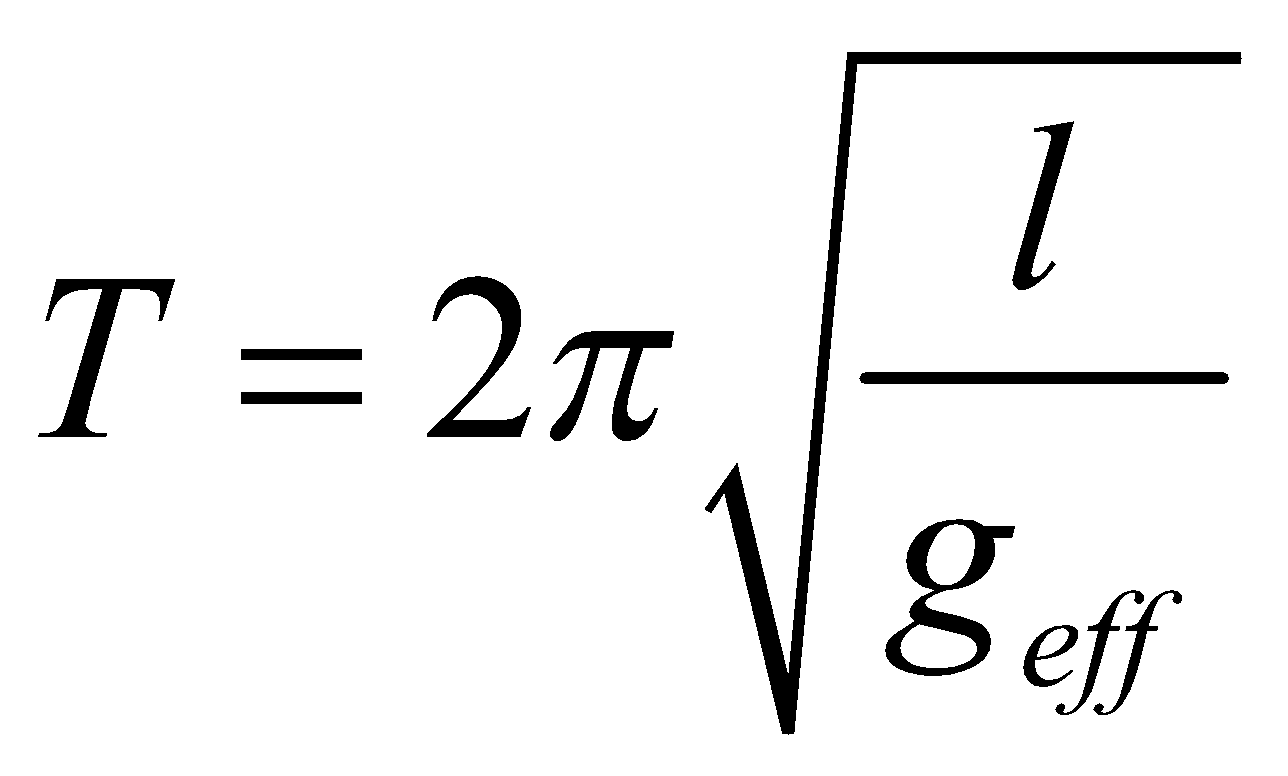
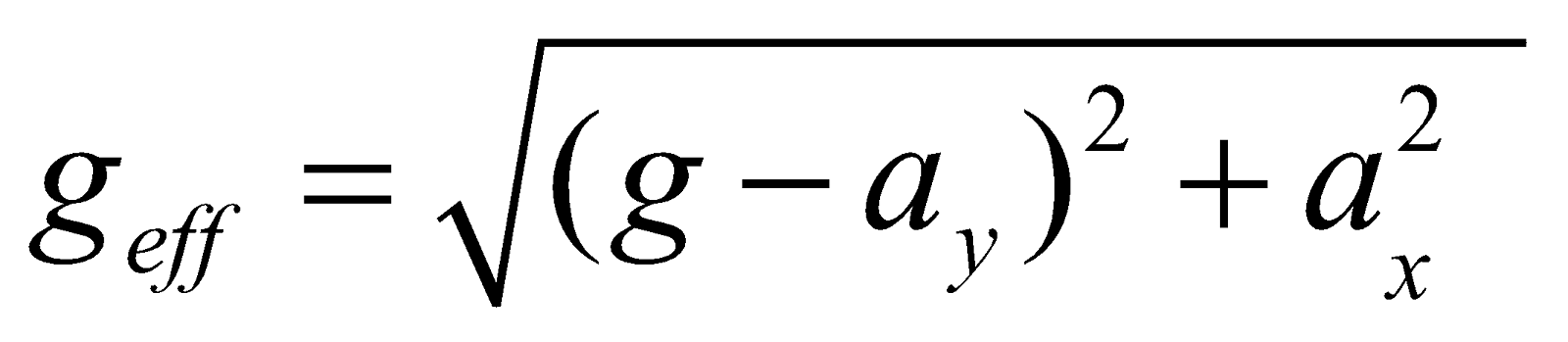
SOME SYSTEMS EXECUTING S.H.M.
- When two springs having force constants k1 and k2 connected in parallel, then
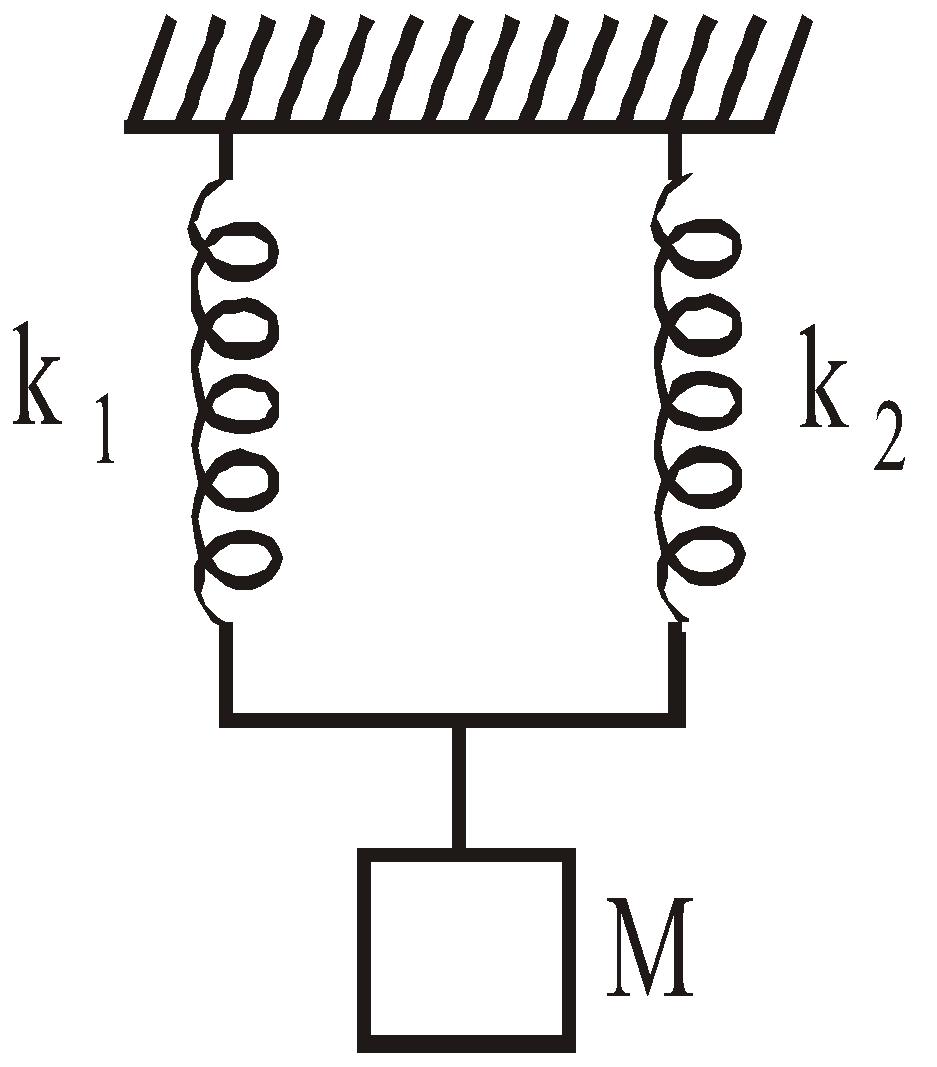
- When two springs of force constants k1 and k2 are connected in series, then
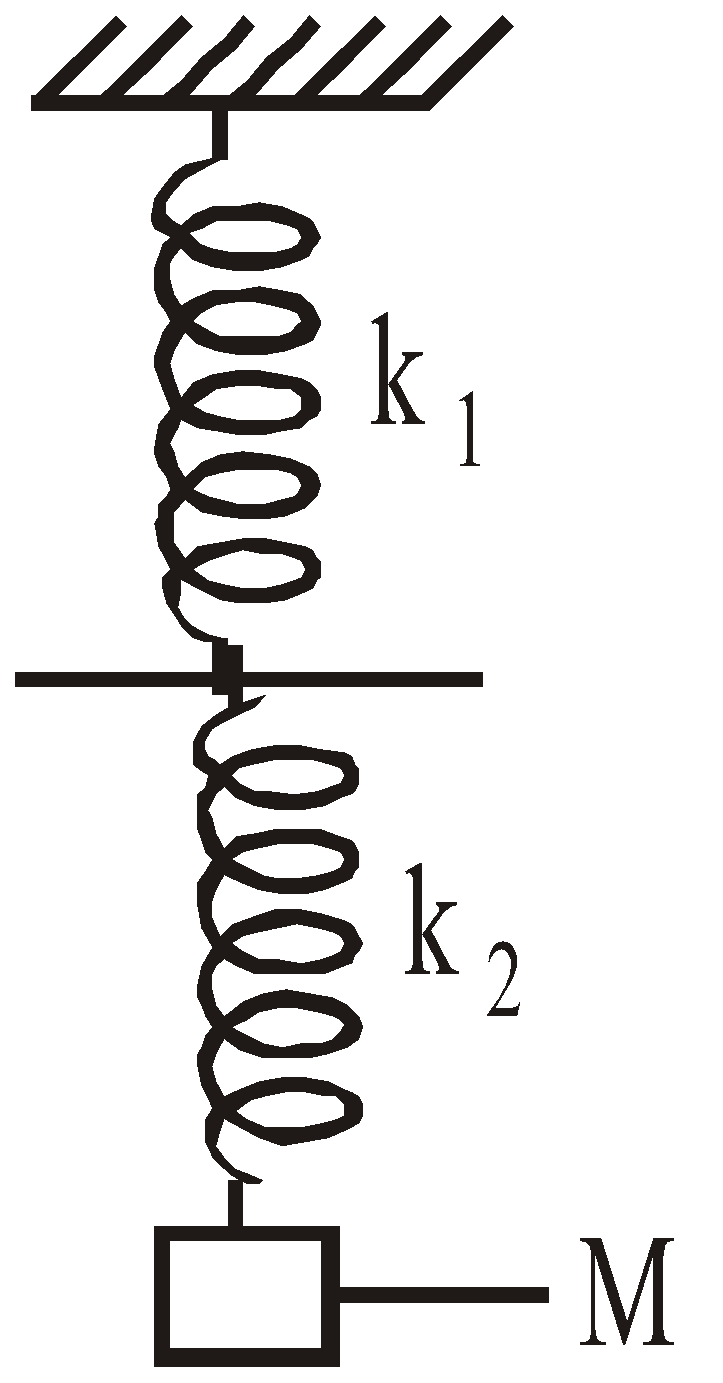
- If two mass M1 and M2 are connected at the two ends of the spring, then their period of oscillation is given by
- When the length of spring increases, spring constant decreases. If the length of spring becomes n times, its spring constant becomes
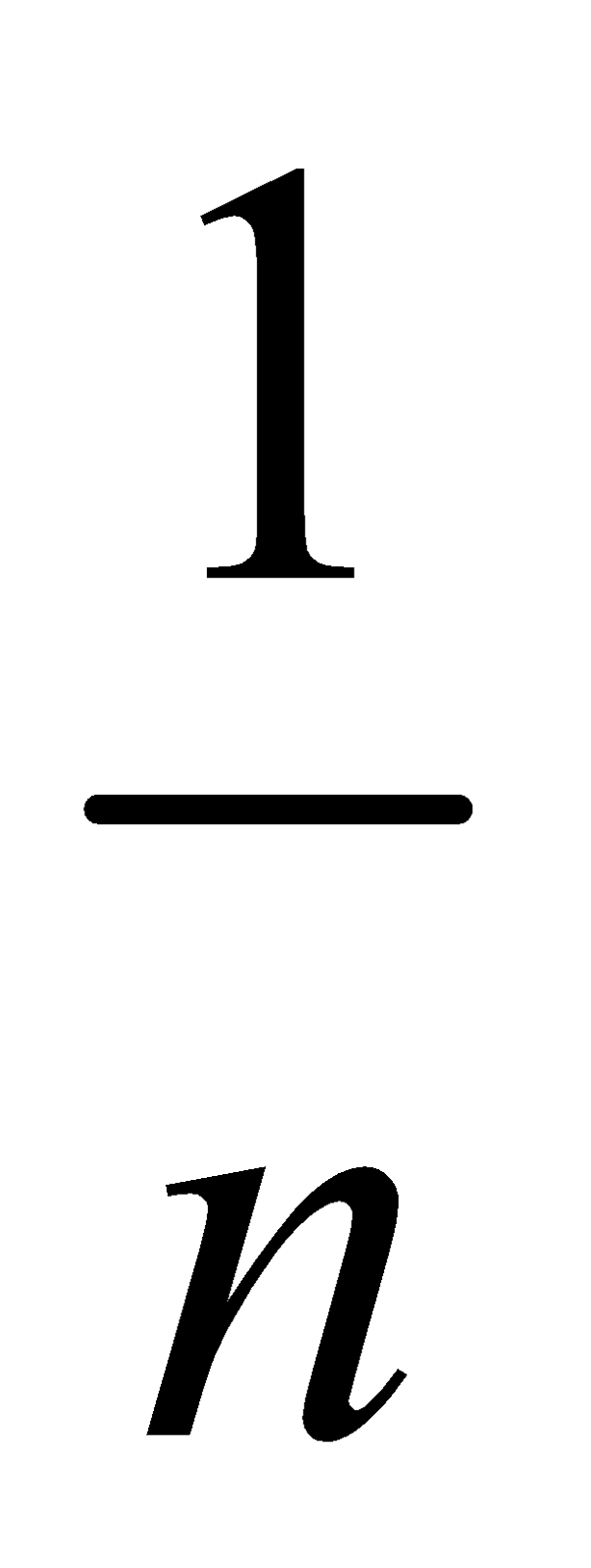 times and therefore time period will be increased by
times and therefore time period will be increased by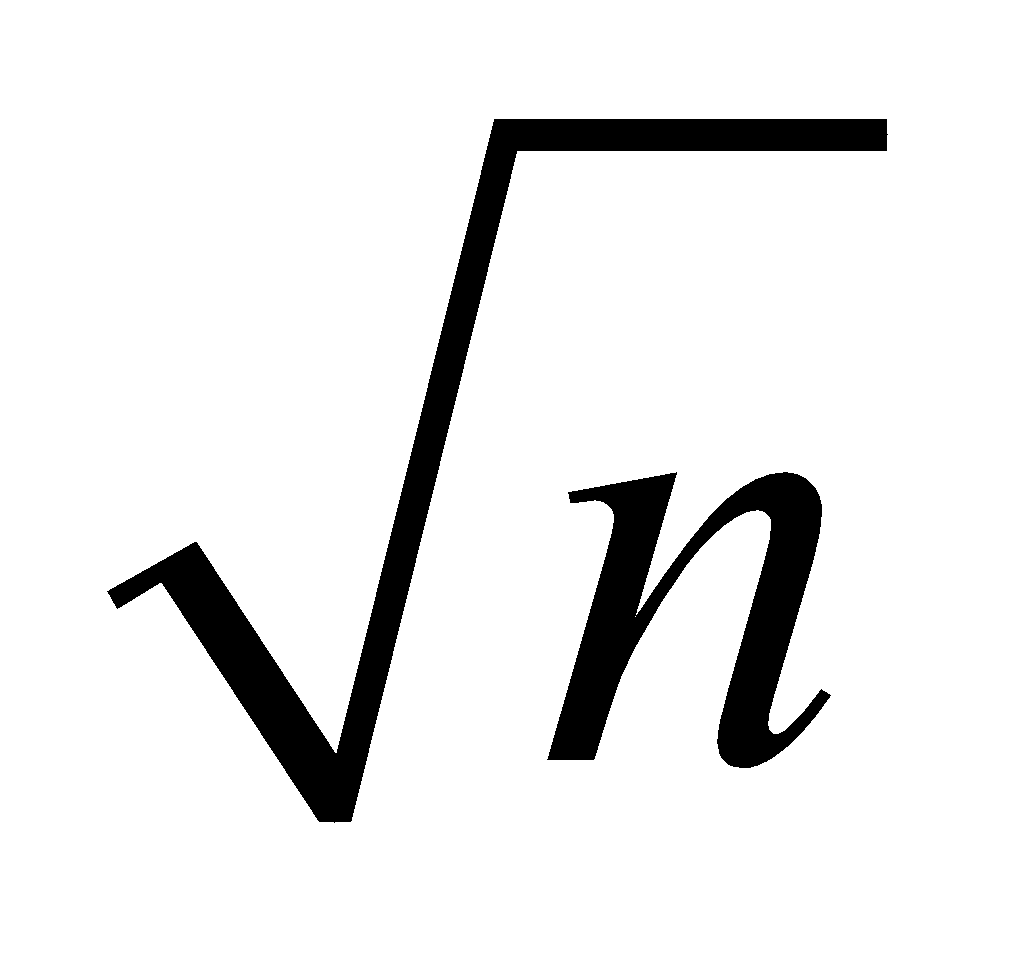 times.
times. - If we divide the spring into n equal parts, the spring constant of each part becomes n k. Hence time period when the same mass is suspended from each part is:
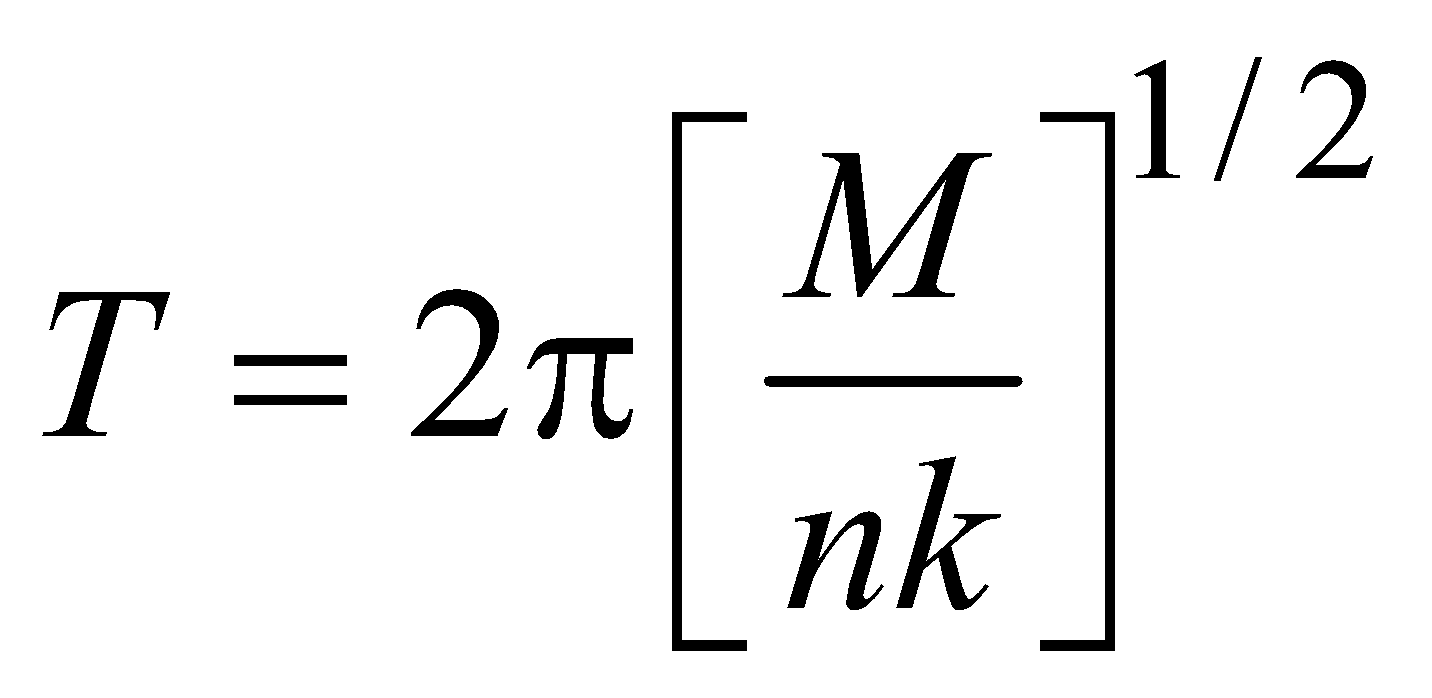
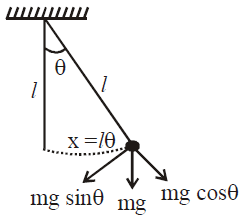
sin θ ≈ θ, so from equation (i)
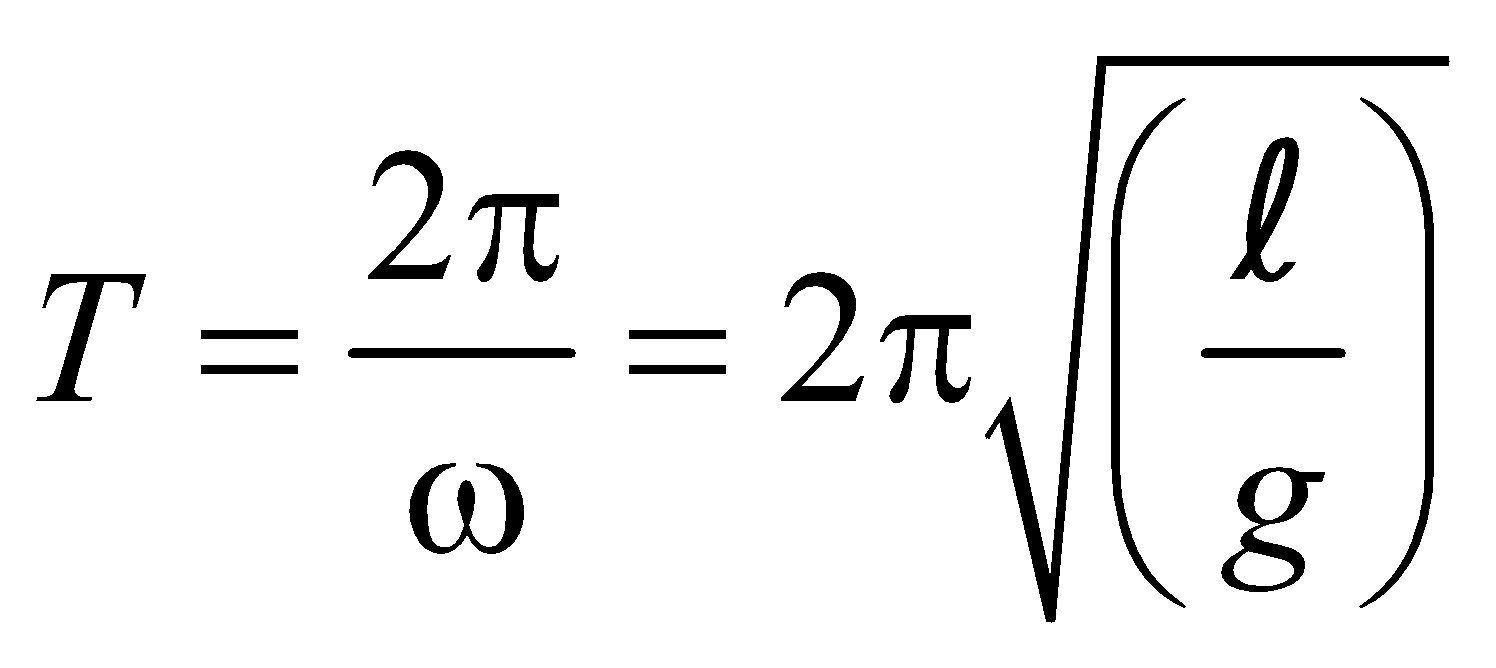
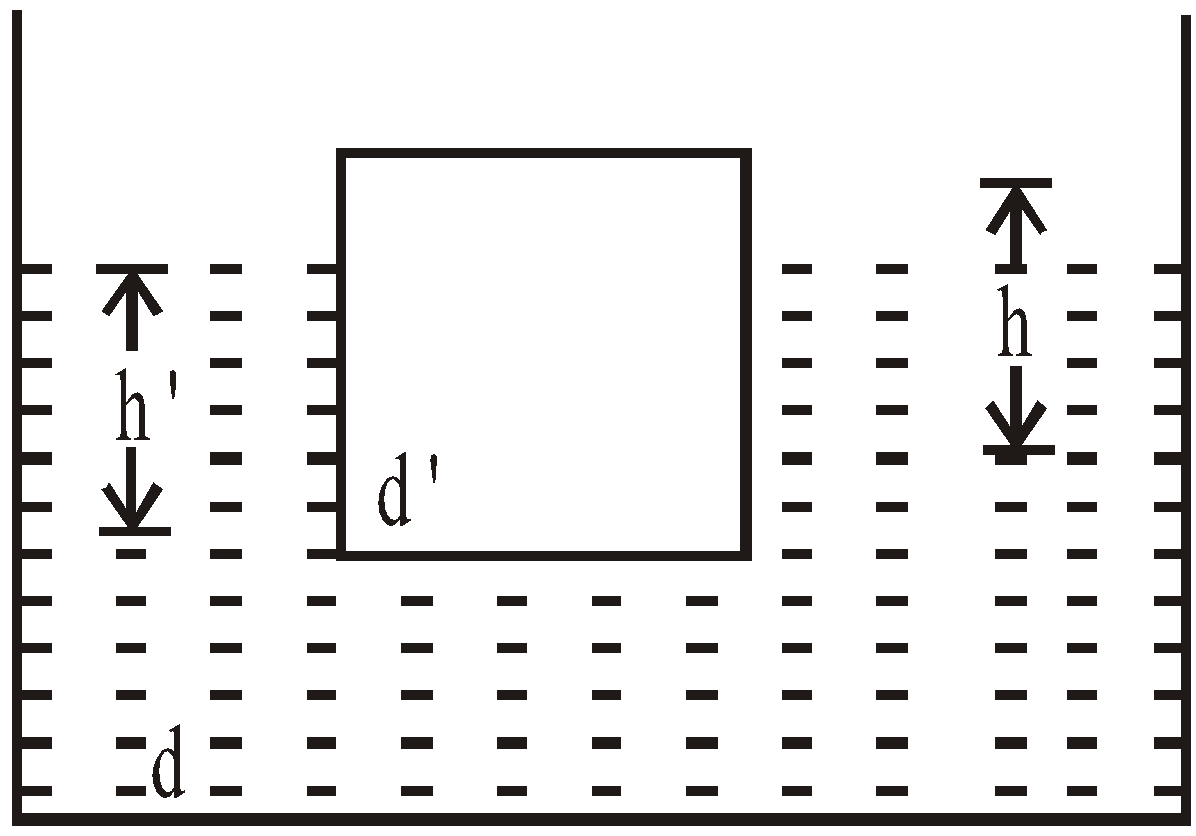
where d = density of liquid, d′ = density of block, h = height of block

- In S.H.M. the phase relationship between displacement, velocity and acceleration, is as follows :
- The velocity is leading the displacement by a phase
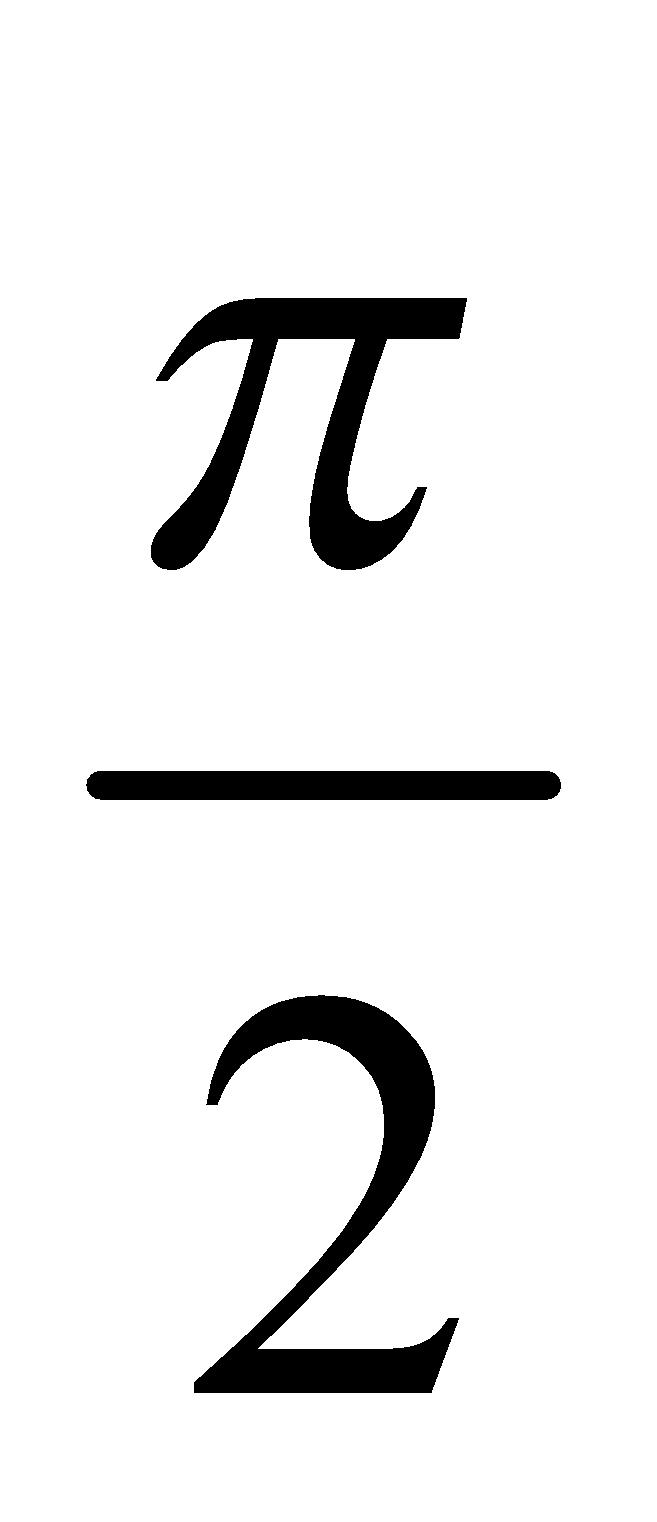 radian
radian - The acceleration is leading the displacement by a phase π radian
- The acceleration is leading the velocity by a phase
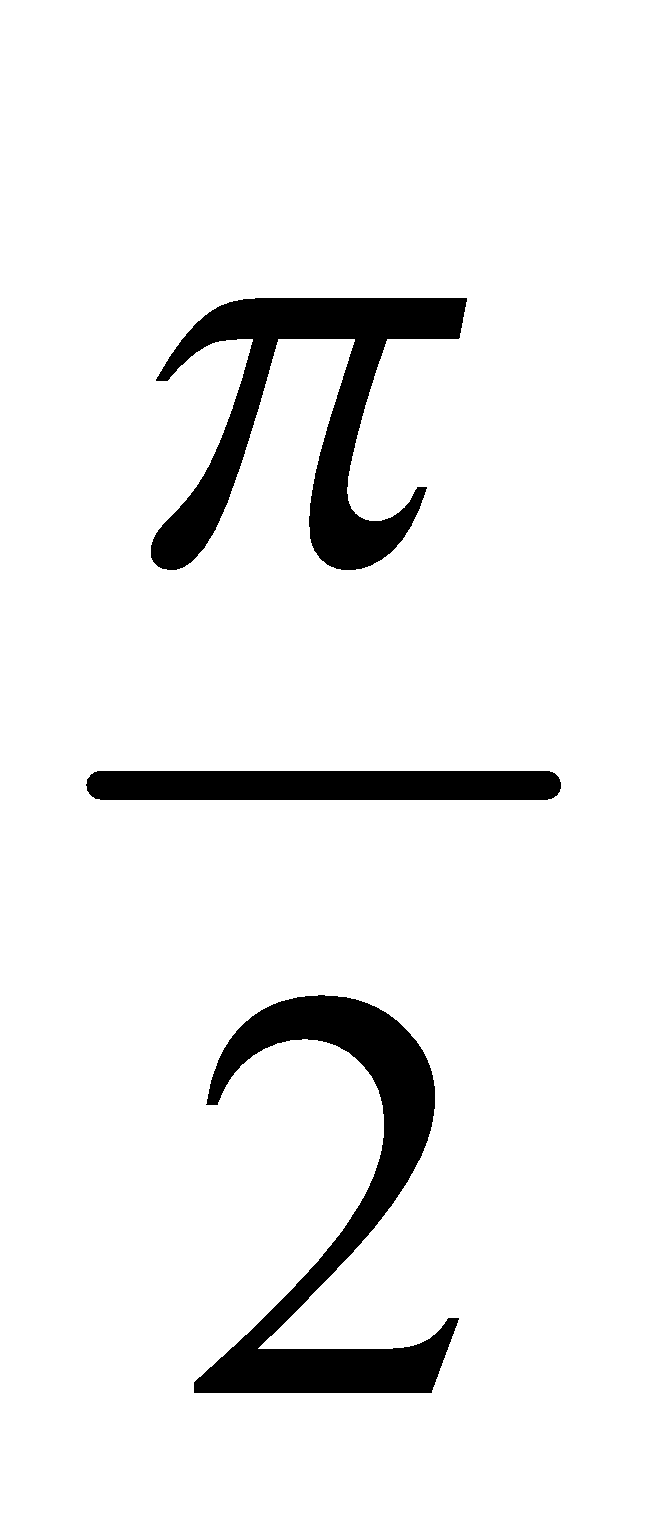 radian.
radian. - When
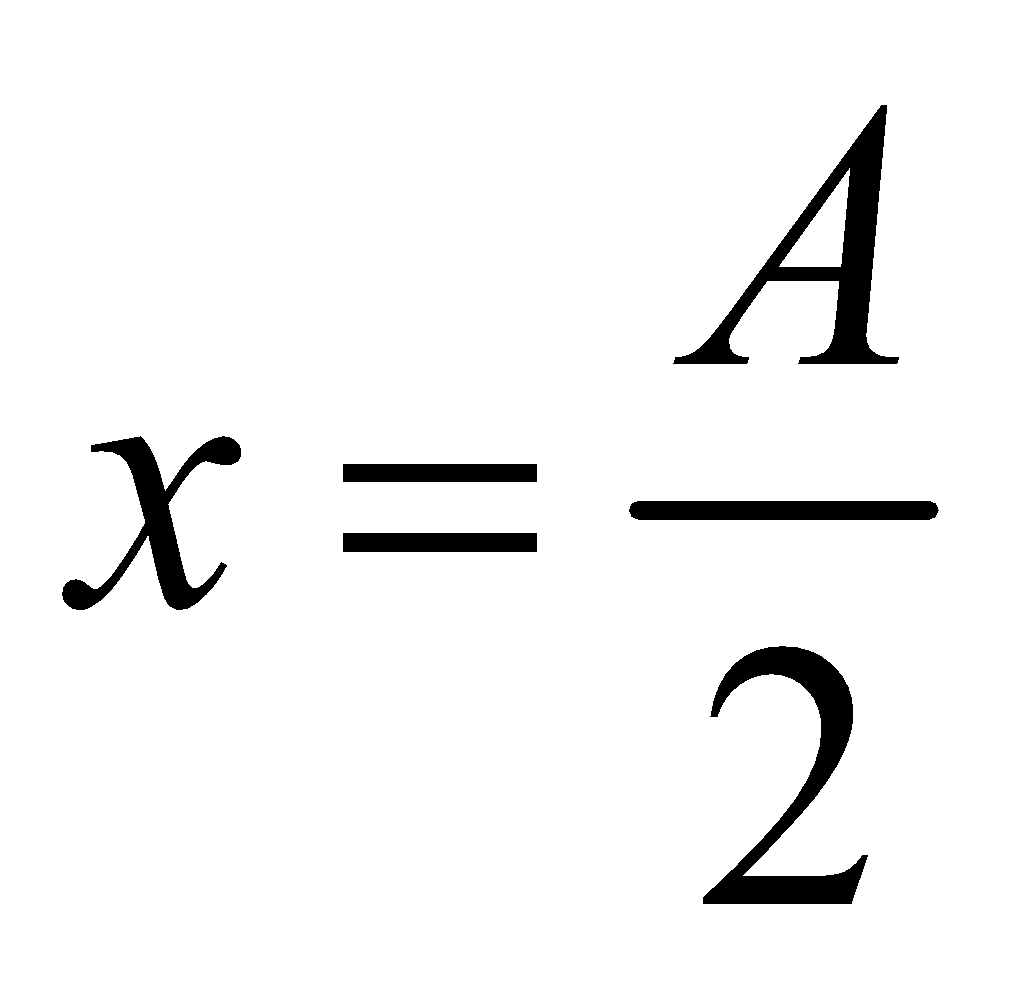 , then velocity V = 0.86Vmax.
, then velocity V = 0.86Vmax. - When V = Vmax/2, the displacement x = 0.87A.
- When
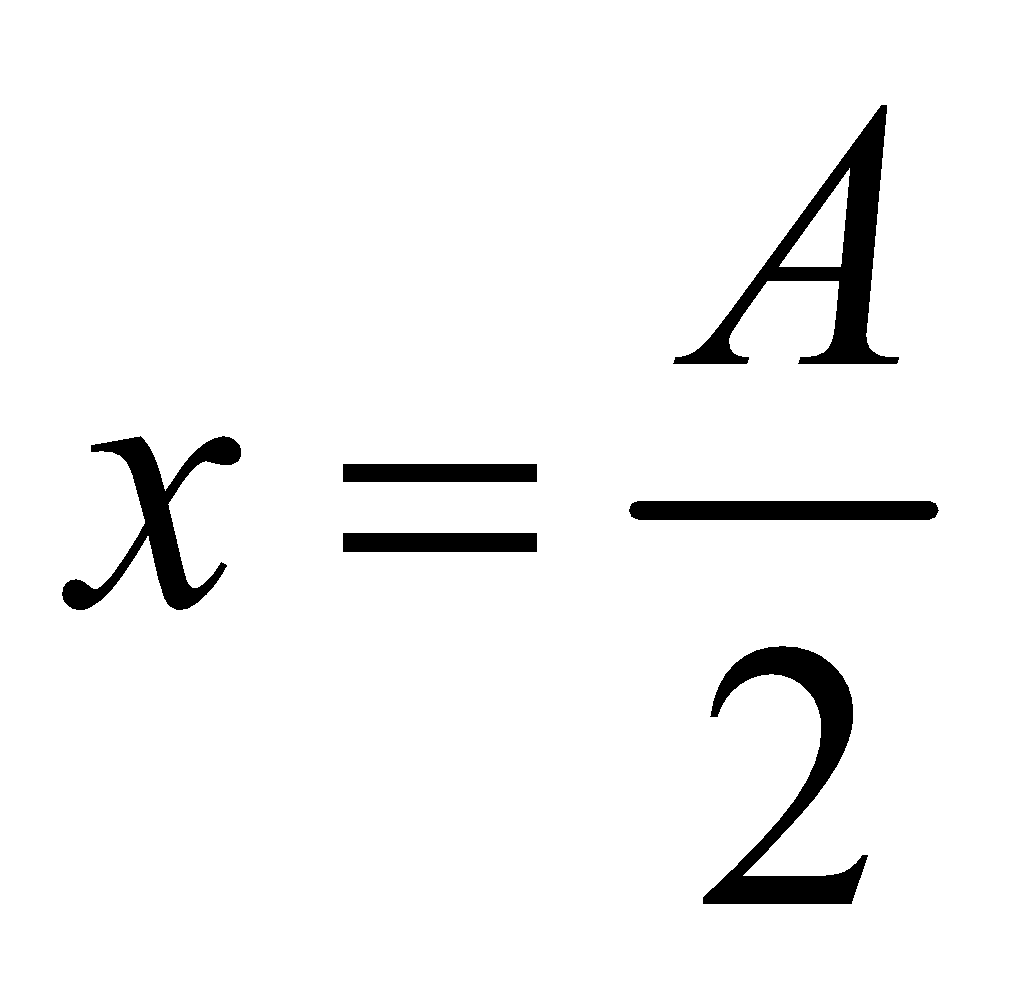 , the kinetic energy of S.H.M. is 75% of the total energy and potential energy 25% of the total energy.
, the kinetic energy of S.H.M. is 75% of the total energy and potential energy 25% of the total energy. - When the kinetic energy of S.H.M. is 50% of the total energy, the displacement is 71% of the amplitude.
- The time period of a simple pendulum of length l which is comparable with radius of earth.
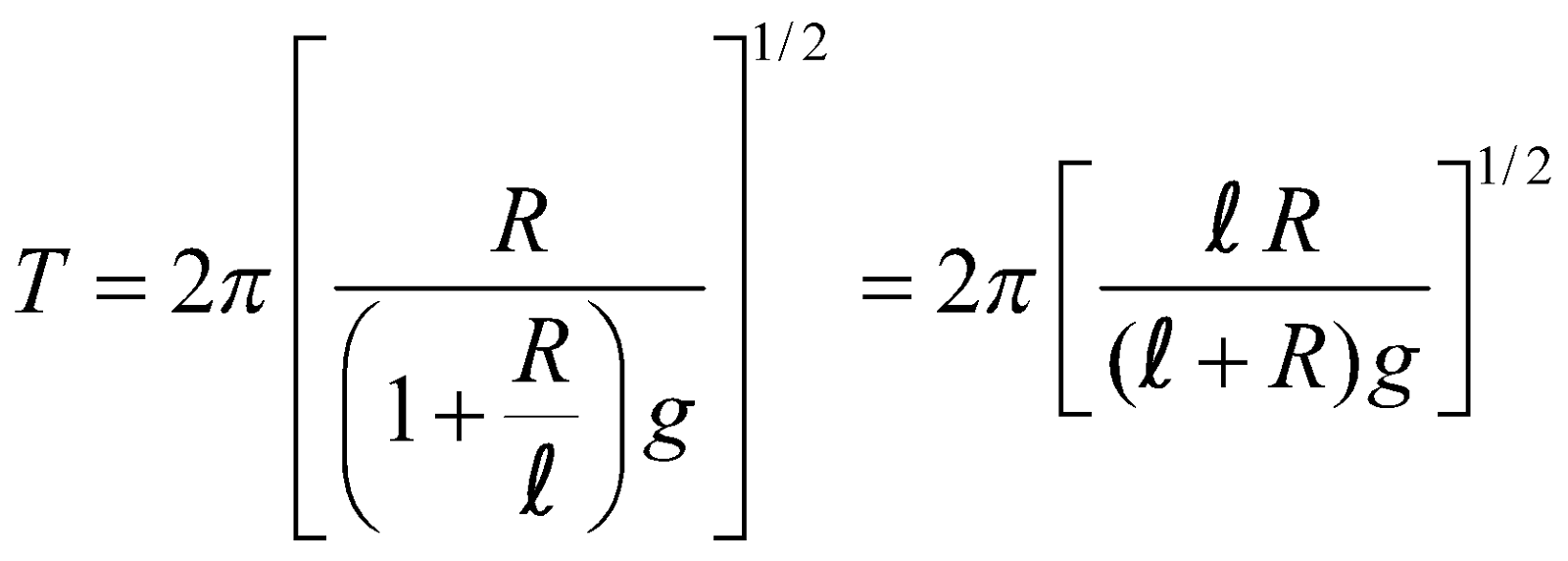
- When l << R, then
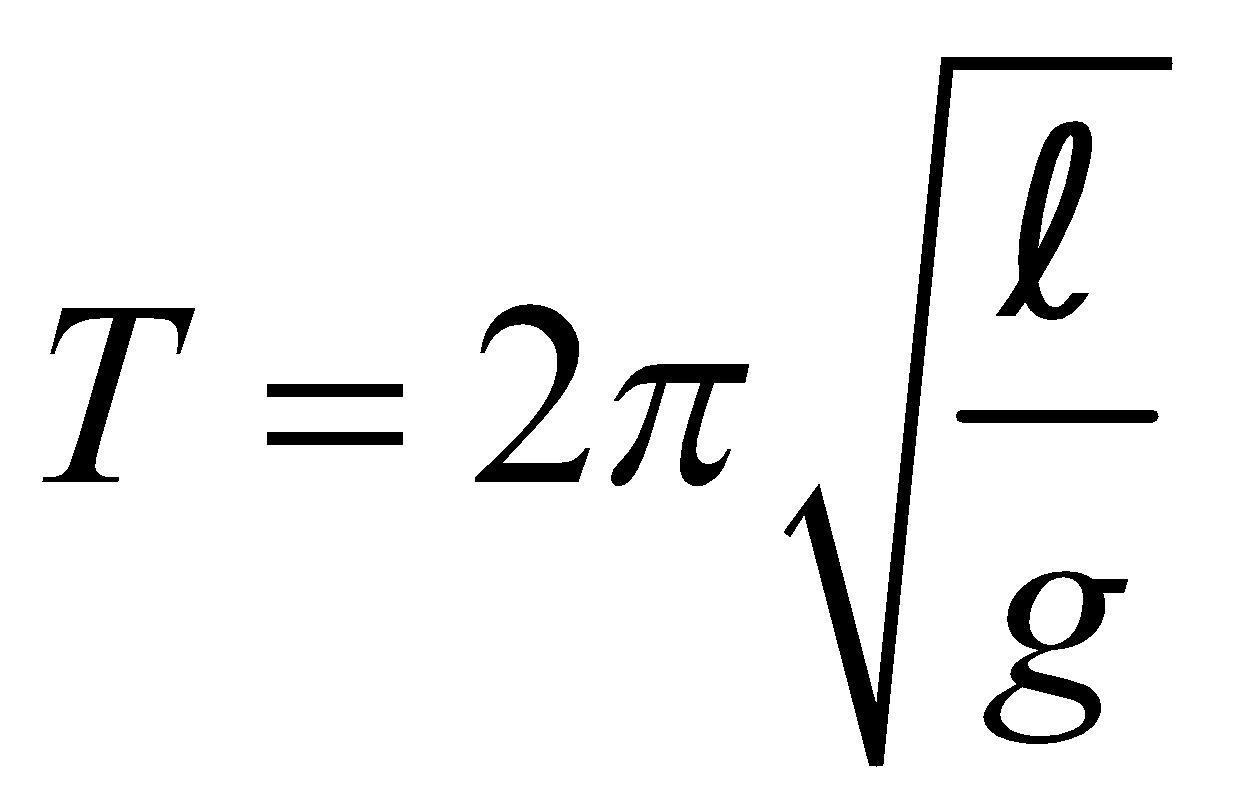
- When l = R, we find
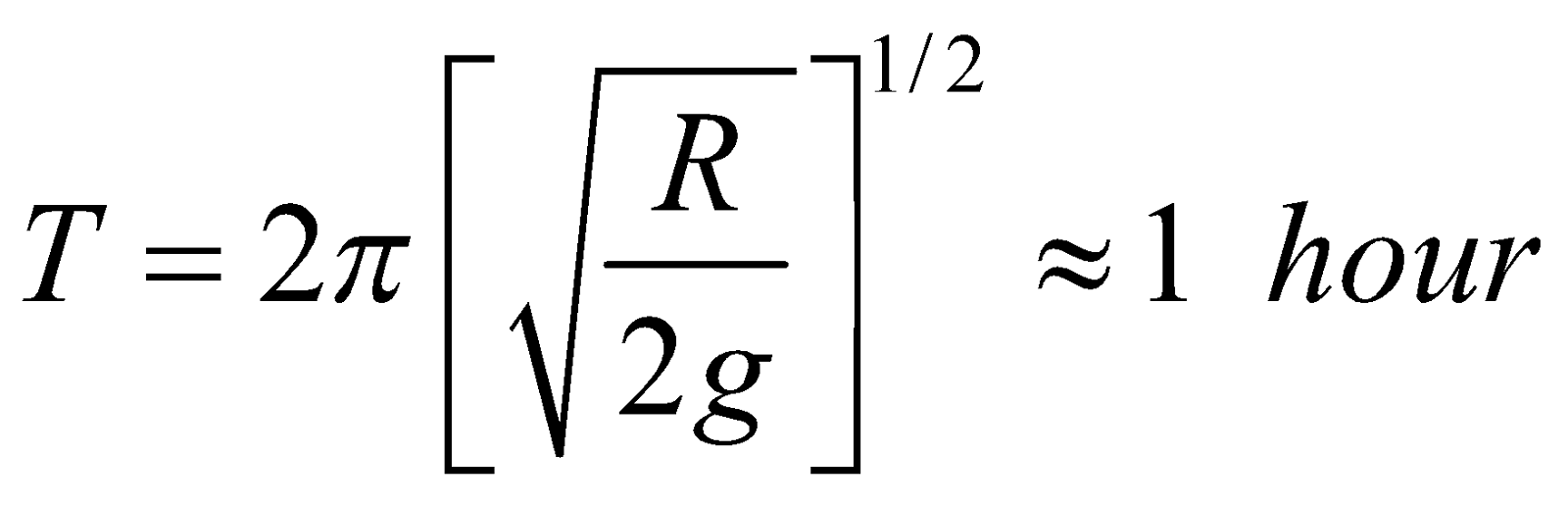
- When l =
 , then
, then
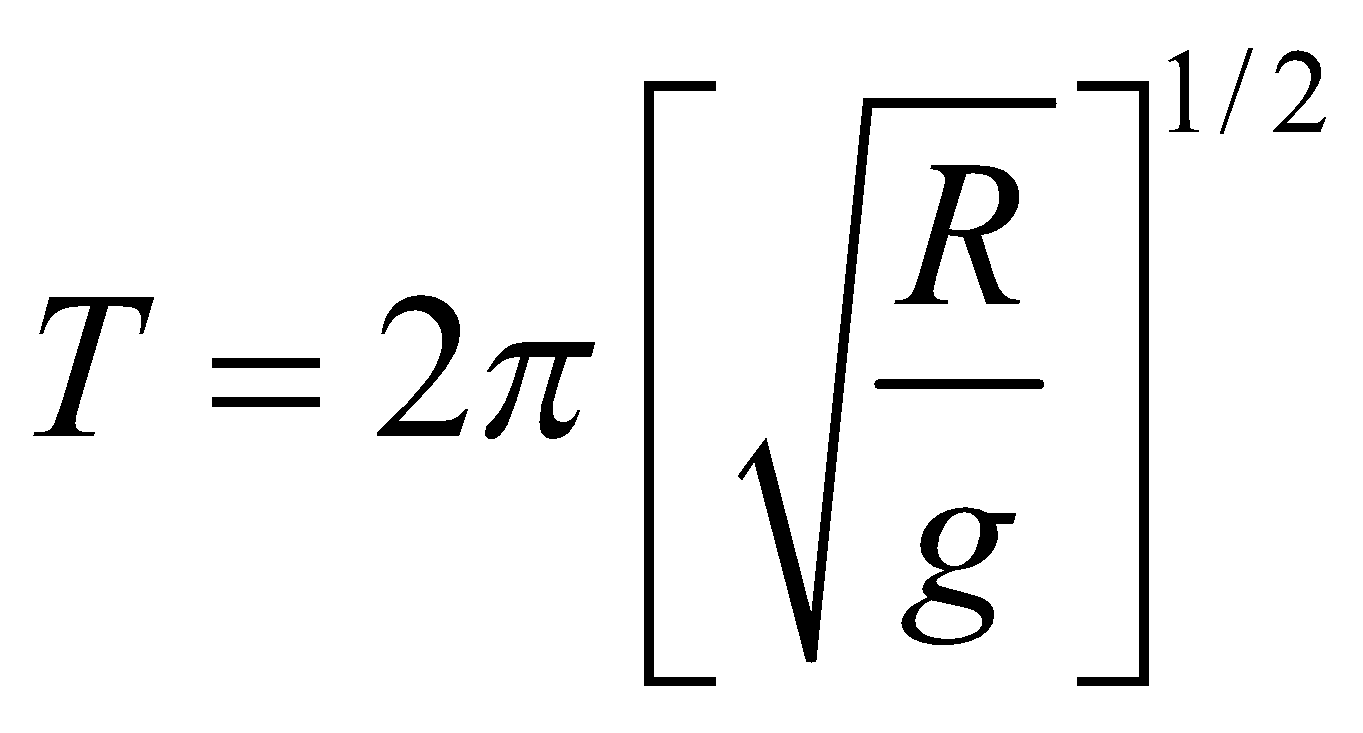 = 84.6 minutes. Thus maximum of T is 84.6 minutes.
= 84.6 minutes. Thus maximum of T is 84.6 minutes.- Under weightlessness or in the freely falling lift
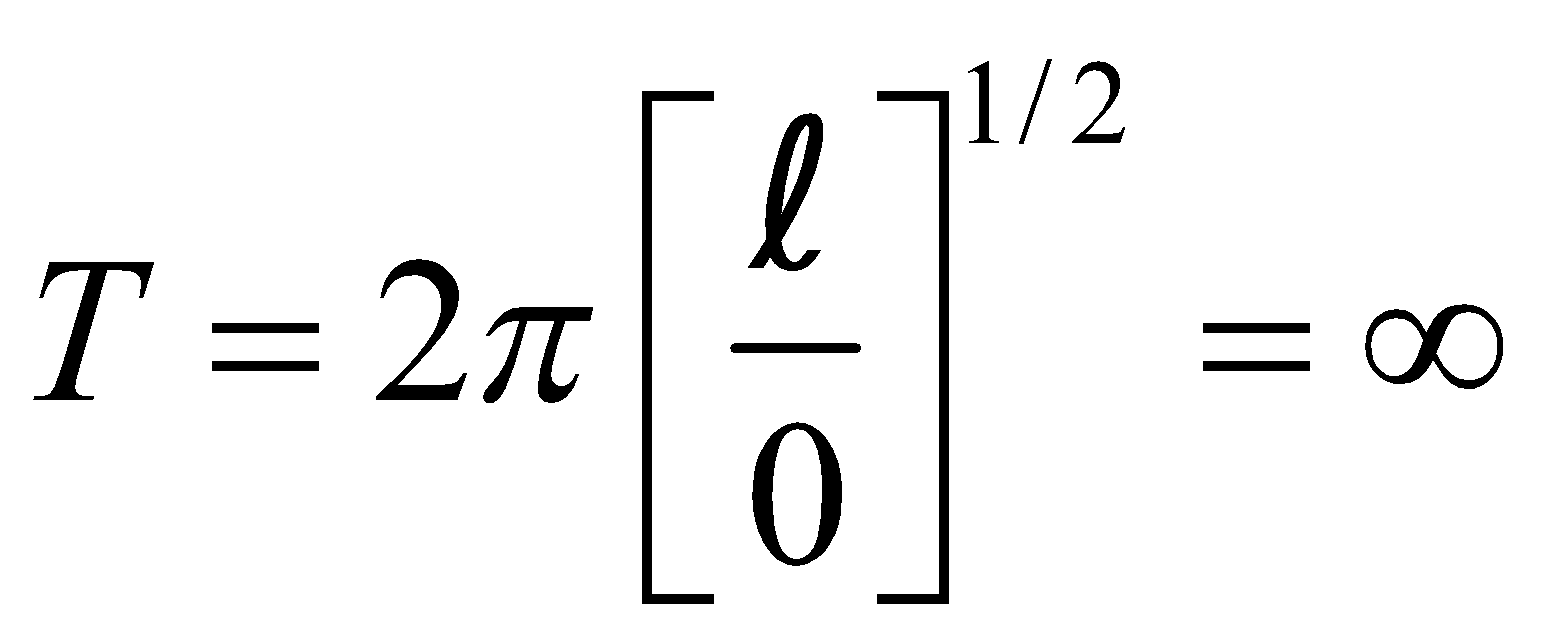
This means, the pendulum does not oscillate at all.
- Time period of a simple pendulum in a train accelerating or retarding at the rate a is given by
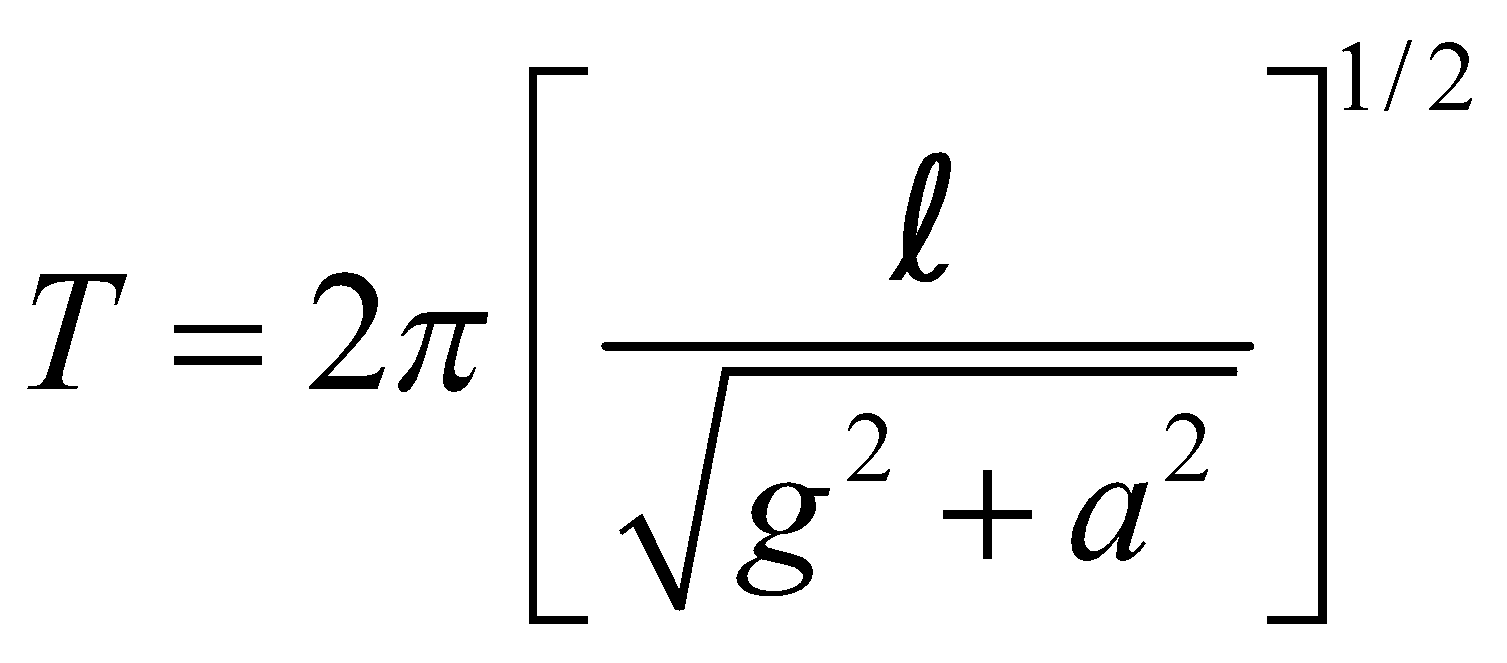
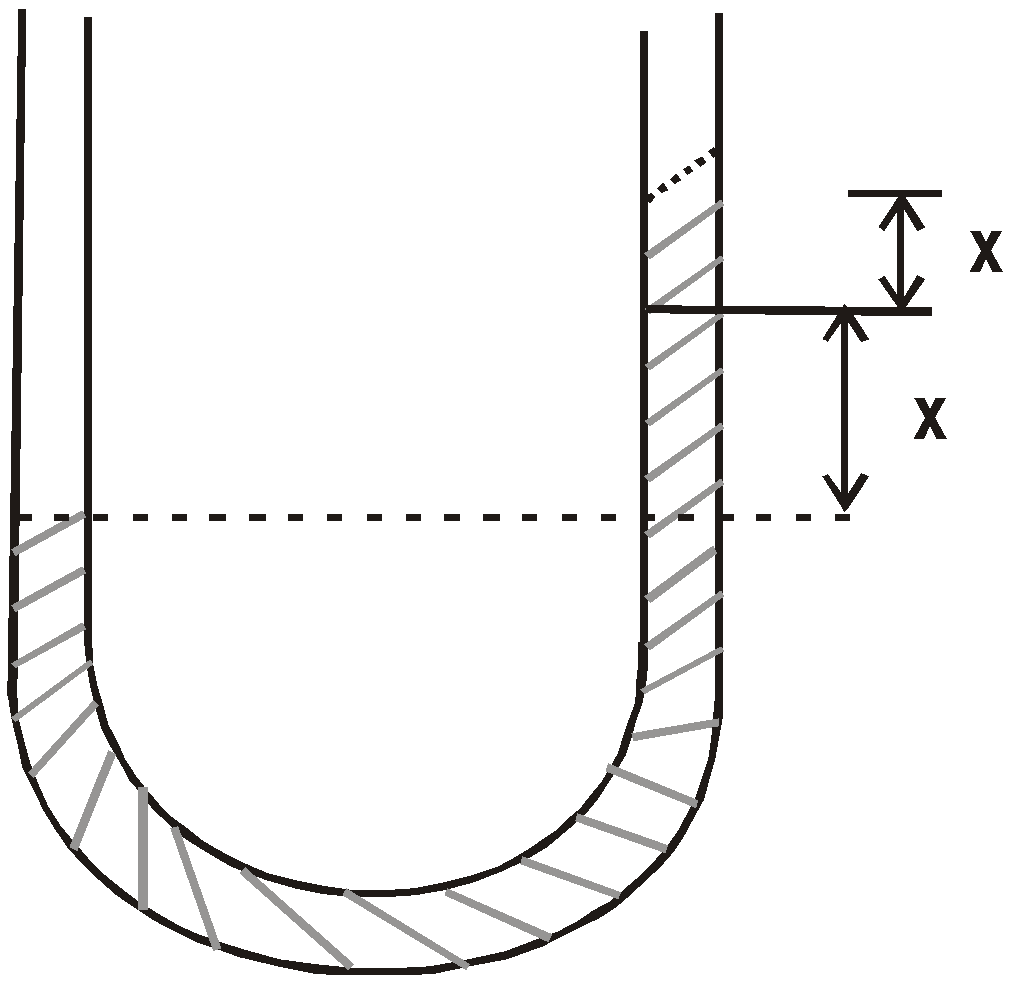
- If a simple pendulum whose bob is of density do is made to oscillate in a liquid of density d, then its time period of vibration in liquid will increase and is given by
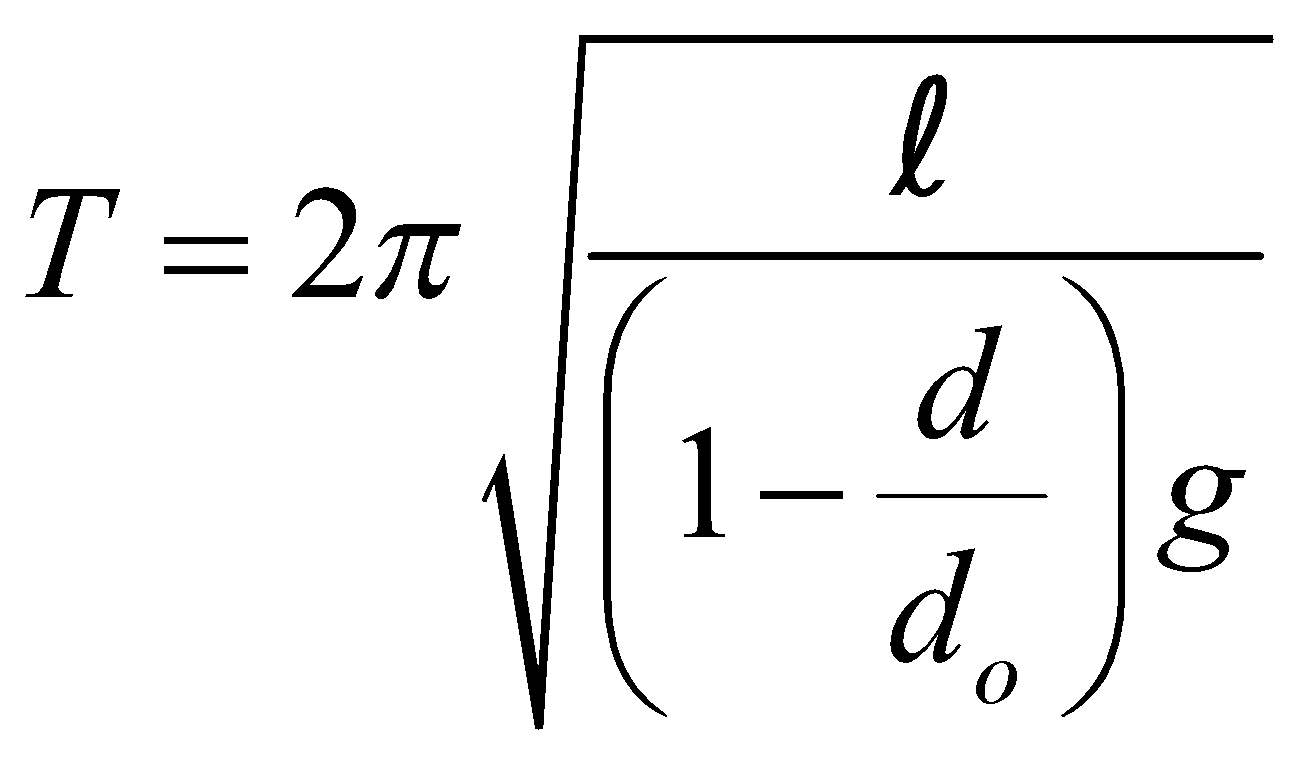 (where d0 > d)
(where d0 > d)- The time period of a simple pendulum in a vehicle moving along a circular path of radius r and with constant velocity V is given by,
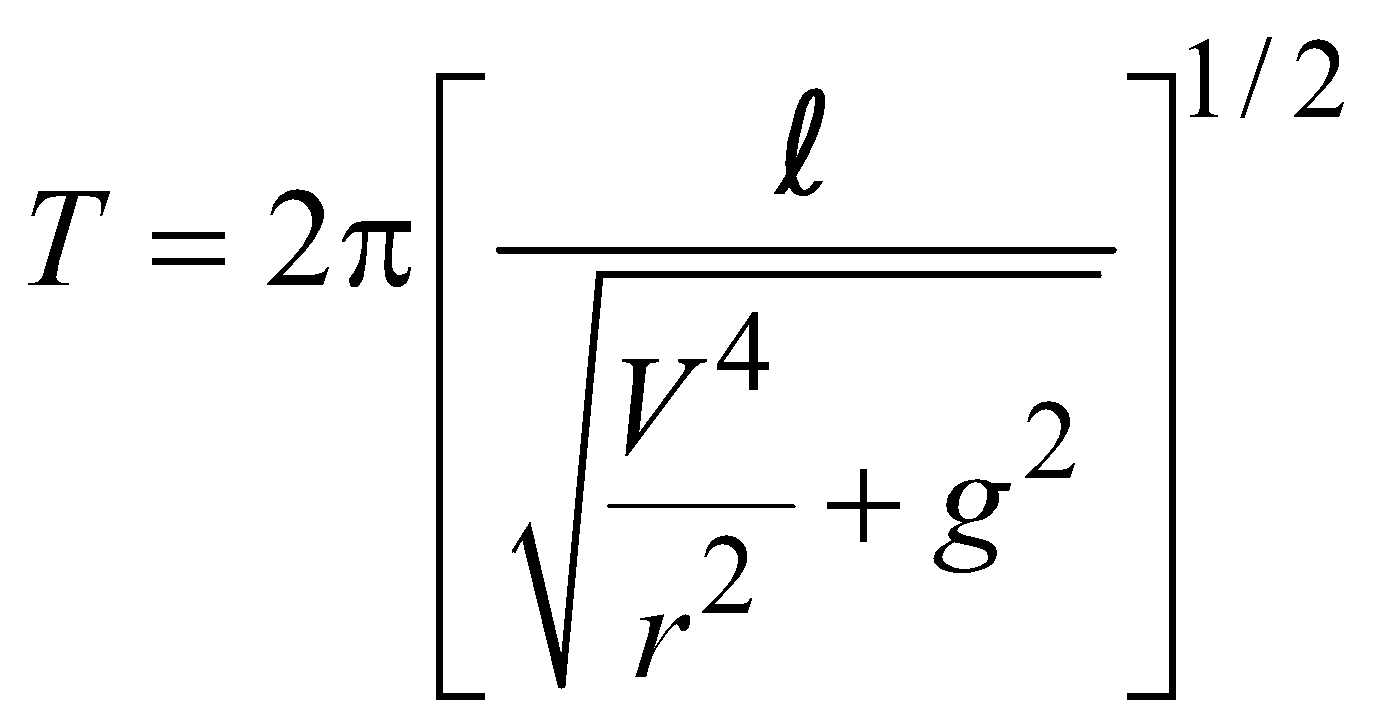
- If T1 and T2 are the time periods of a body oscillating under the restoring force F1 and F2 then the time period of the body under the influence of the resultant force
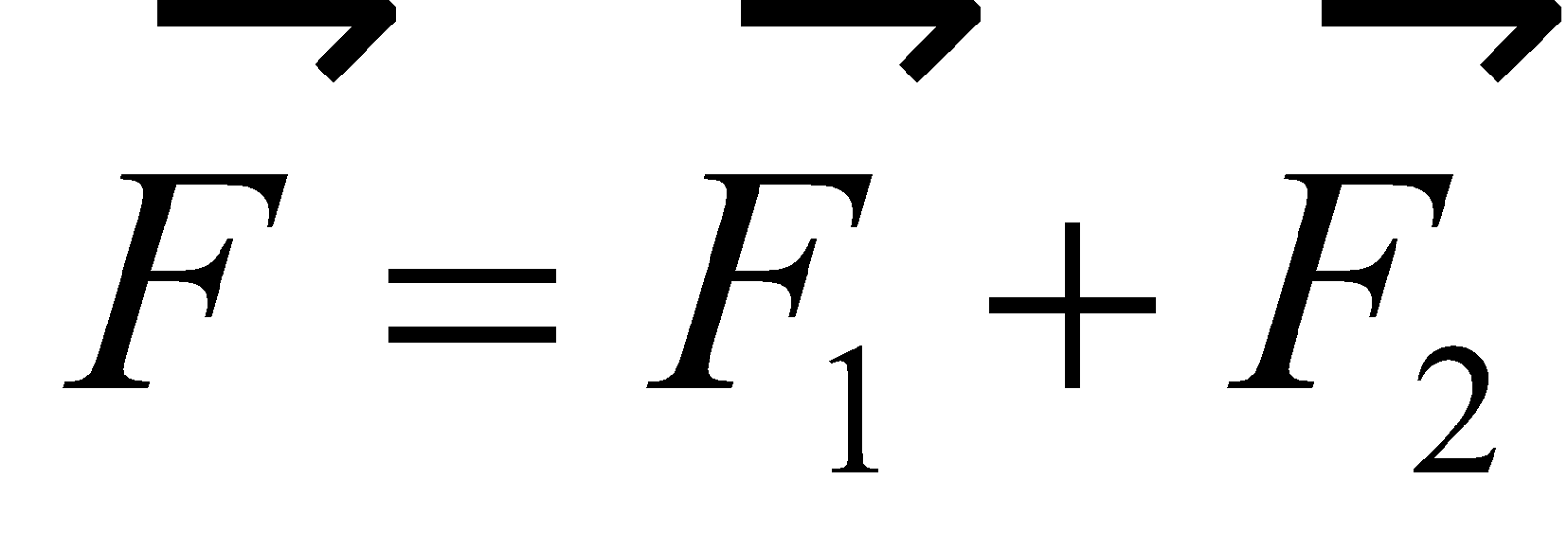 will be
will be 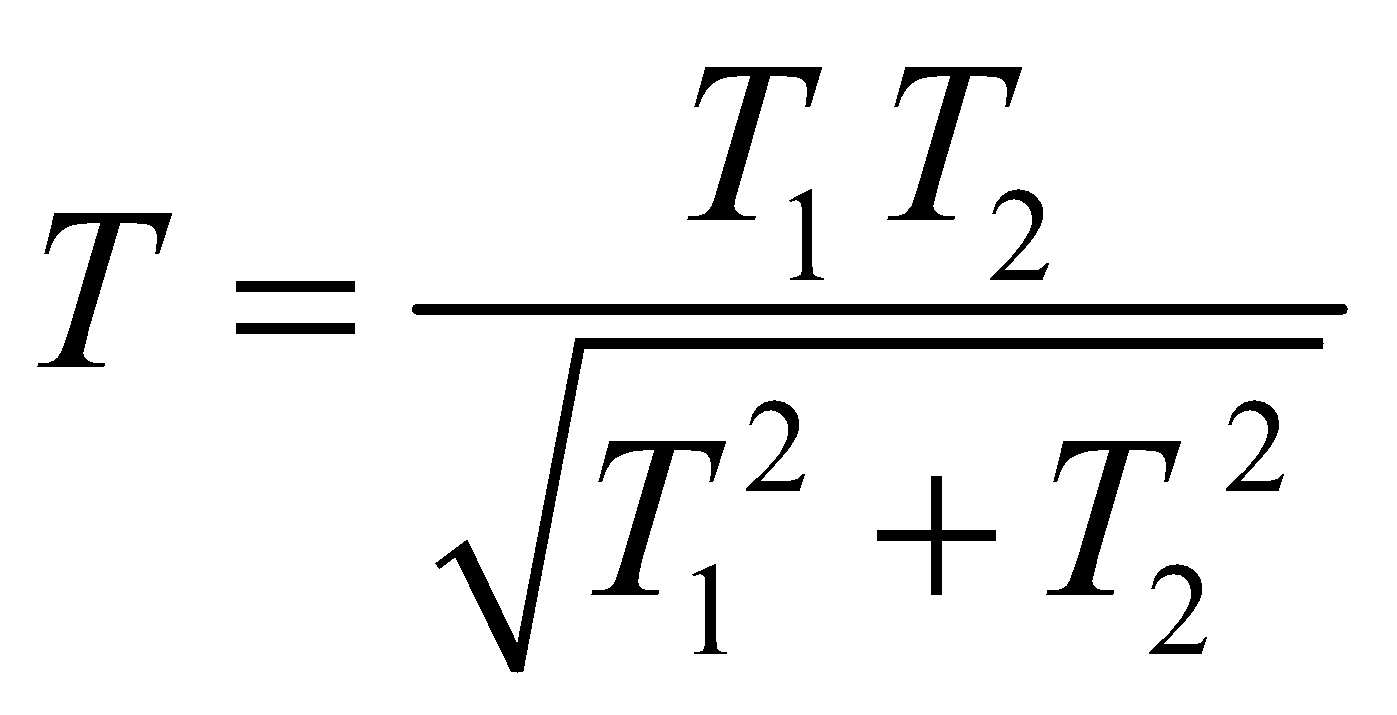
- (a) The percentage change in time period of simple pendulum when its length changes is
- If a wire of length l, area of cross-section A, Young’s modulus Y is stretched by suspending a mass m, then the mass can oscillate with time period
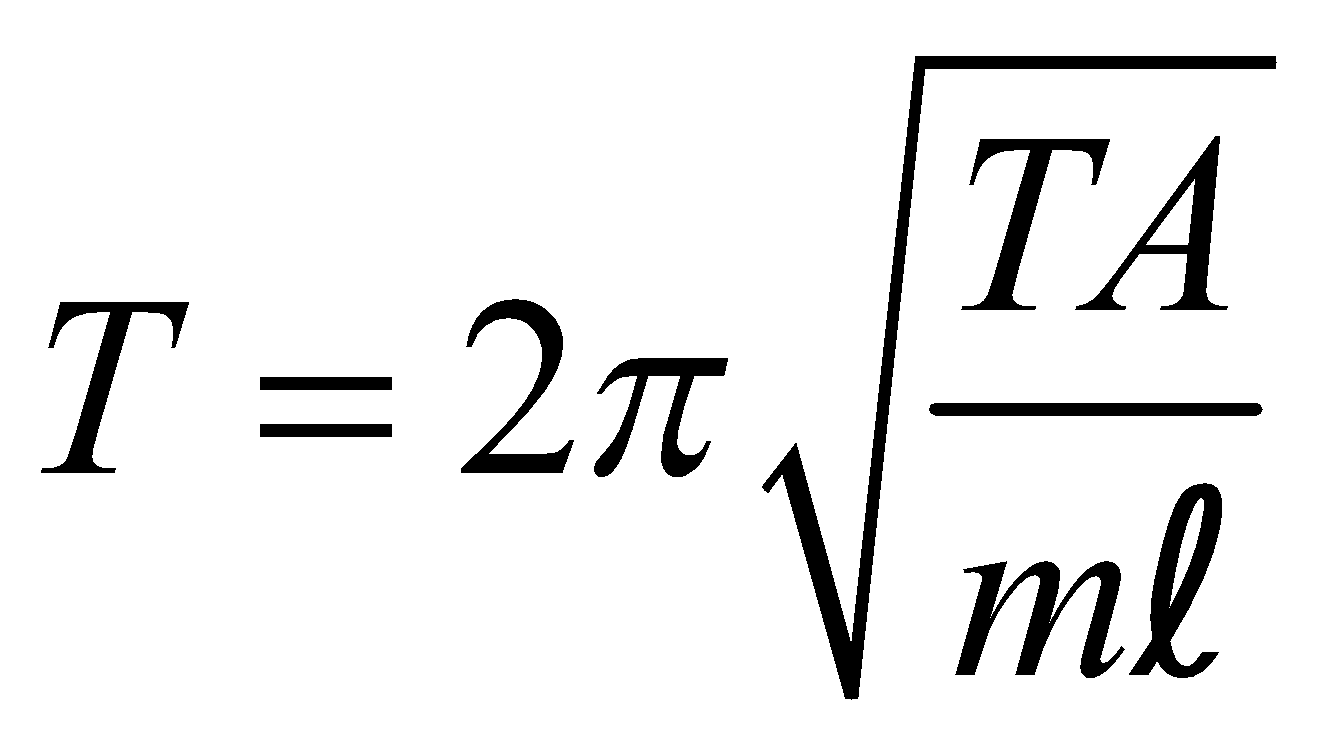
- If a simple pendulum is suspended from the roof of compartment of a train moving down an inclined plane of inclination θ, then the time period of oscillations
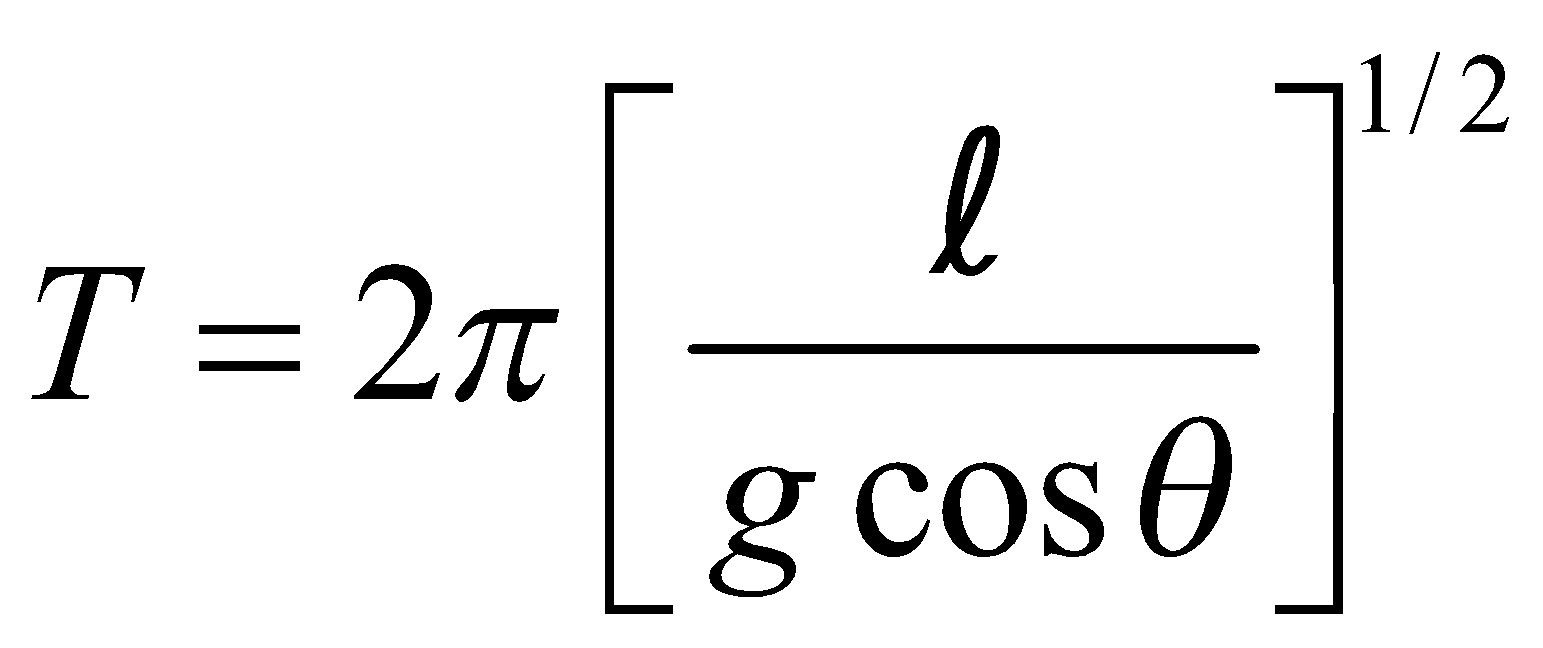
- If a ball of radius r oscillates in a bowl of radius R, then its time period is given by :
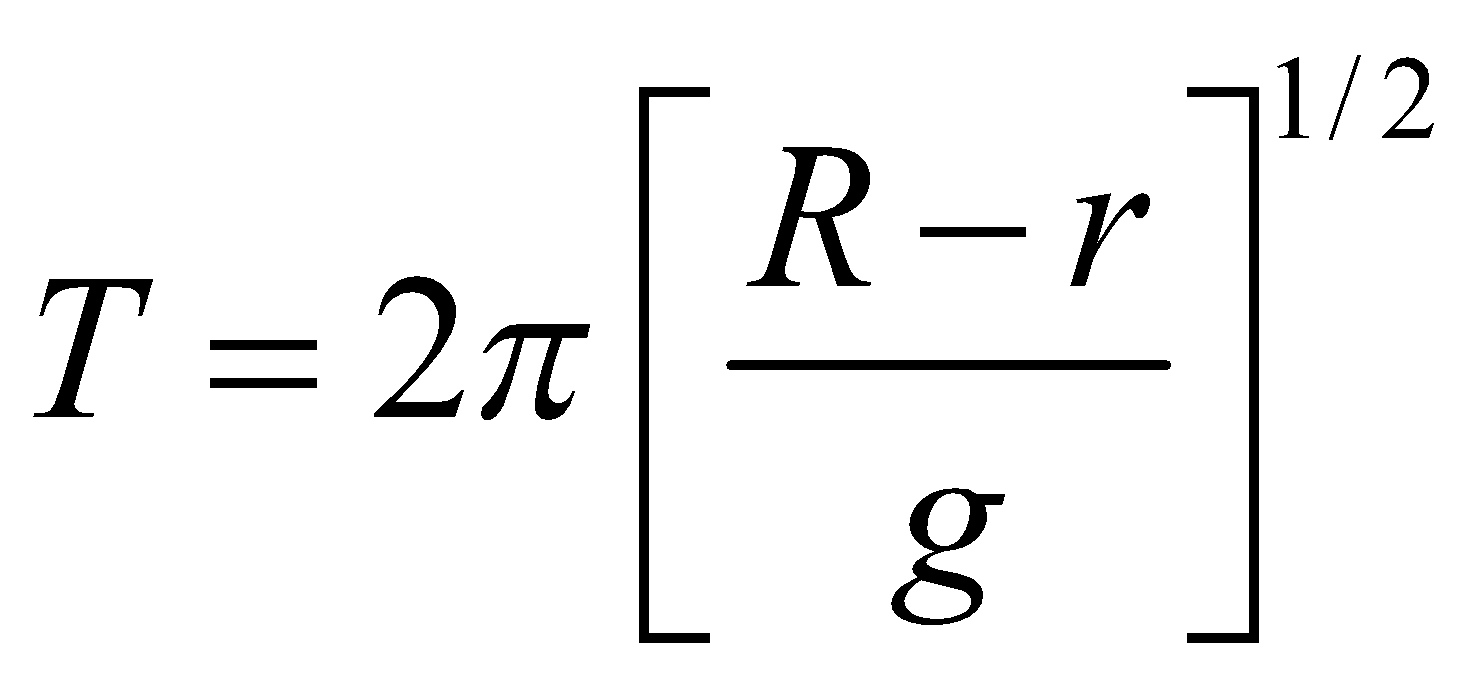
- If a disc of radius r oscillates about a point at its rim, then its time period is given by:
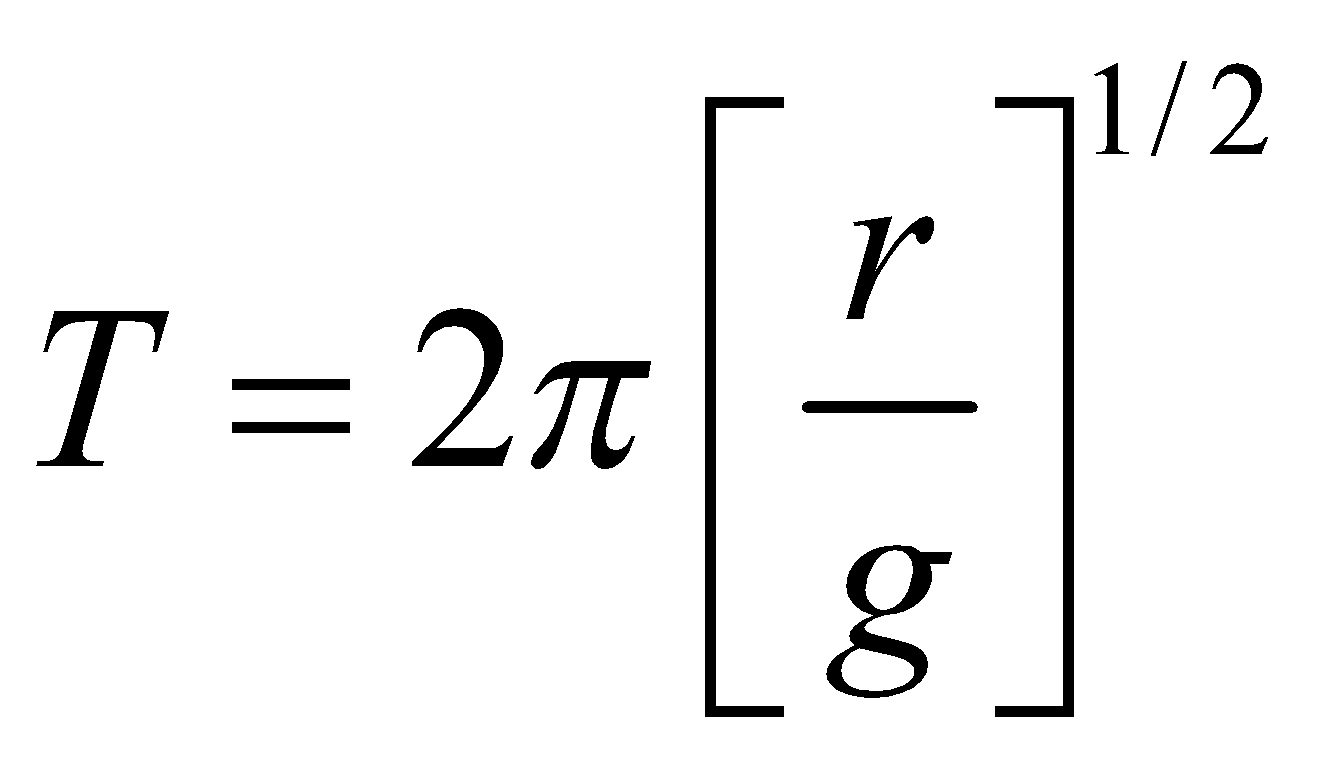
- The graph between the length of a simple pendulum and its time period is a parabola.
- The graph between the length of a simple pendulum and the square of its time period is a straight line.
- The graph between l & T and between l & T2 intersect at T = 1 second.
- The time period of the mass attached to spring does not change with the change in acceleration due to gravity.
- If the mass m attached to a spring oscillates in a non-viscous liquid density σ, then its time period is given by
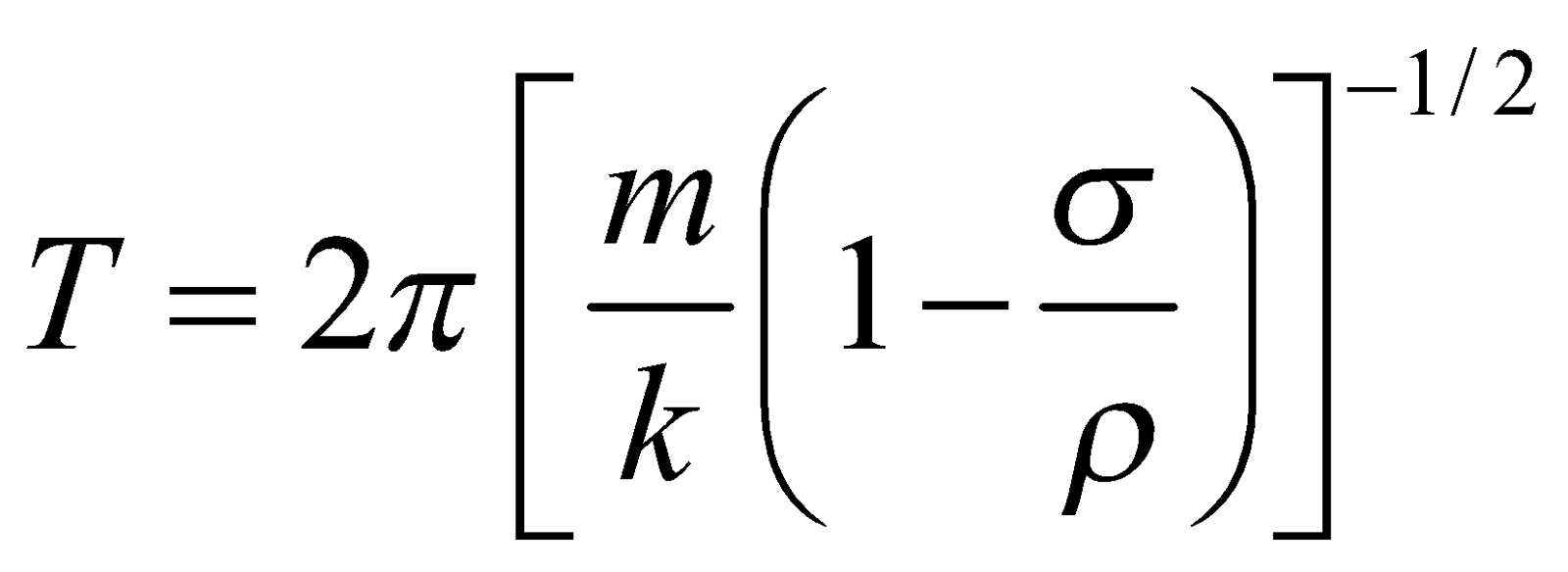
- The length of second pendulum (T = 2 sec) is 99 cm
PHYSICAL PENDULUM

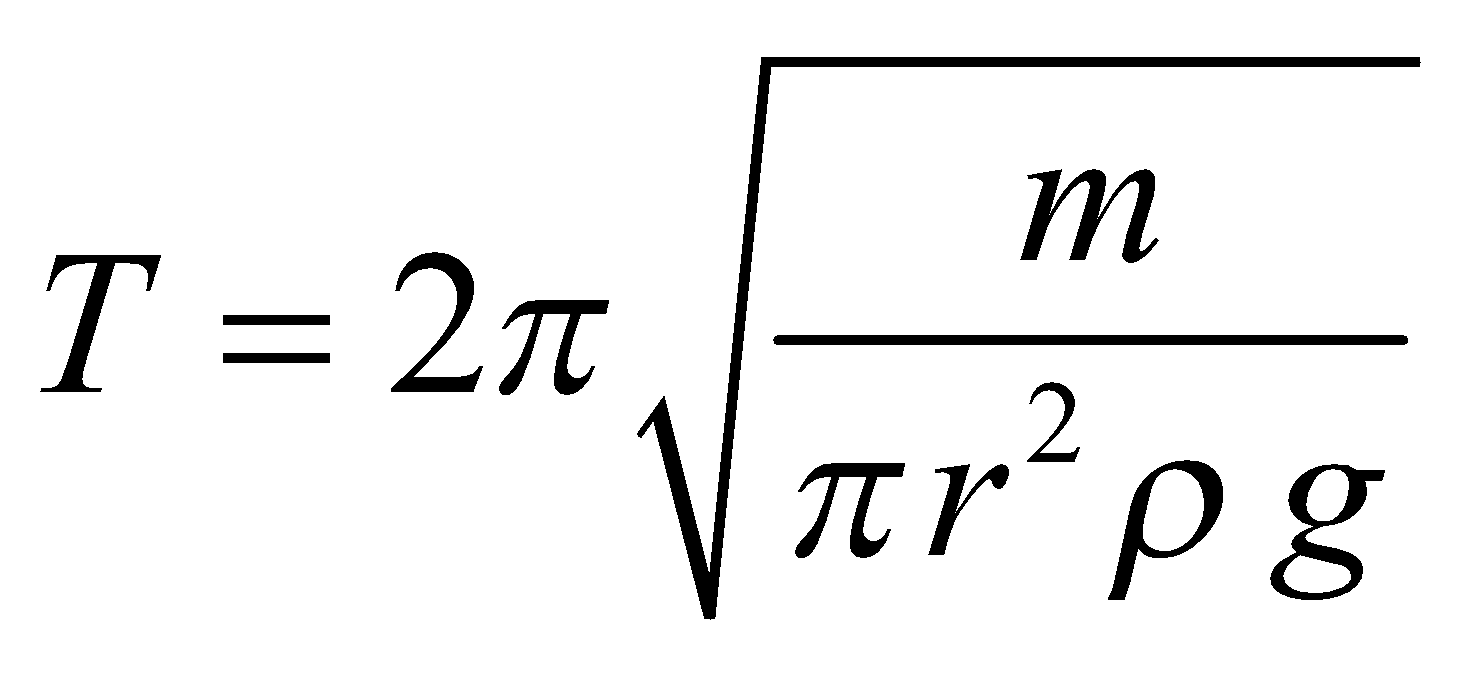
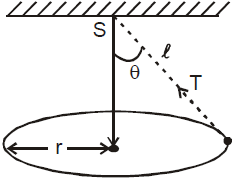
CONICAL PENDULUM
TORSIONAL PENDULUM
- The displacement, velocity and acceleration of S.H.M. vary simple harmonically with the same time period and frequency.
- The kinetic energy and potential energy vary periodically but not simple harmonically. The time period of kinetic energy or potential energy is half that of displacement, velocity and acceleration.
- The graph between displacement, velocity or acceleration and t is a sine curve. But the graph between P.E. or K.E. of S.H.M. and time t is parabola.
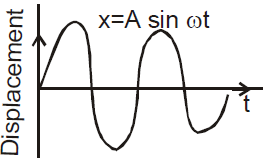

- If the bob of simple pendulum is -vely charged and a +vely charged plate is placed below it, then the effective acceleration on bob increases and consequently time period decreases.
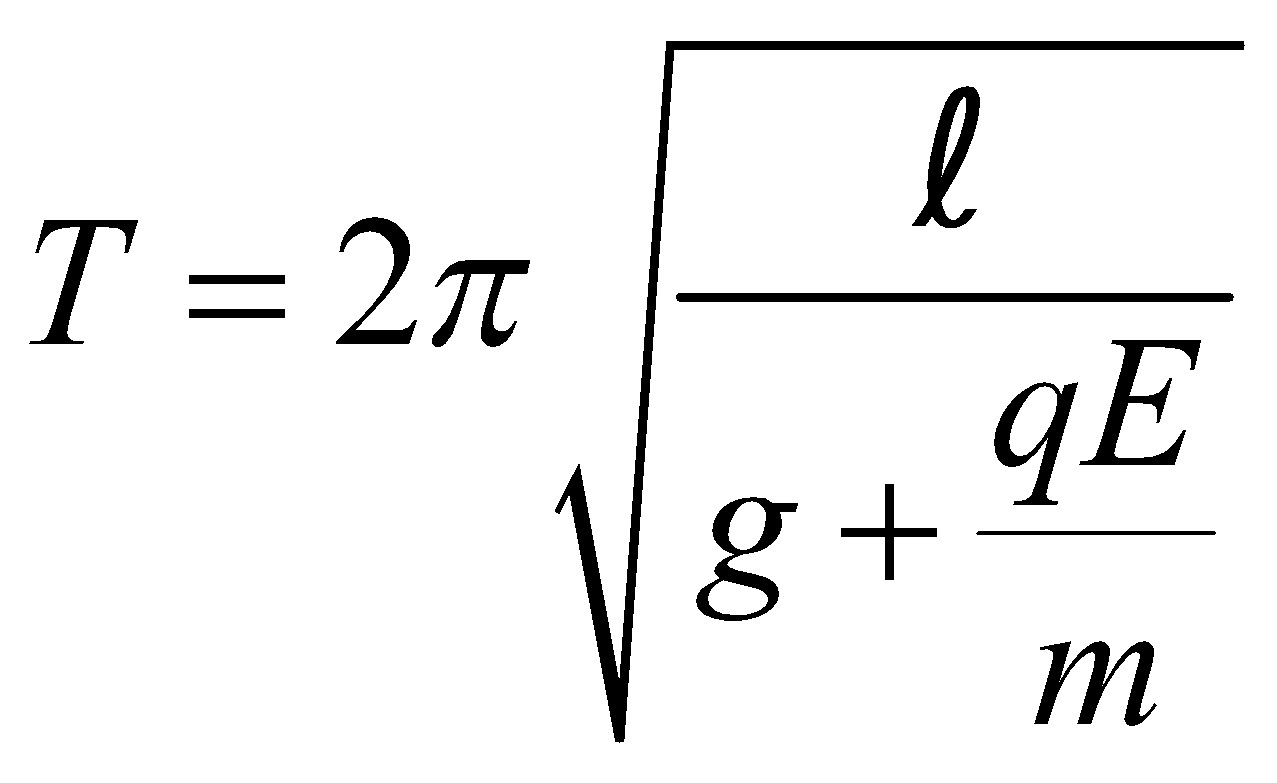
- If the bob of a simple pendulum is -vely charged and is made to oscillate above the -vely charged plate, then the effective acceleration on bob decreases and the time period increases.
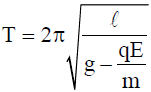
- A pendulum clock slows down in summer and goes faster in winter.
- Potential energy of a particle executing S.H.M. is equal to average force × displacement.
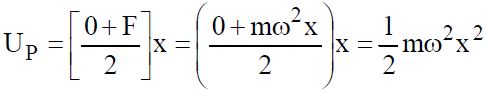
- If the total energy of a particle executing S.H.M. is E, then its potential energy at displacement x is
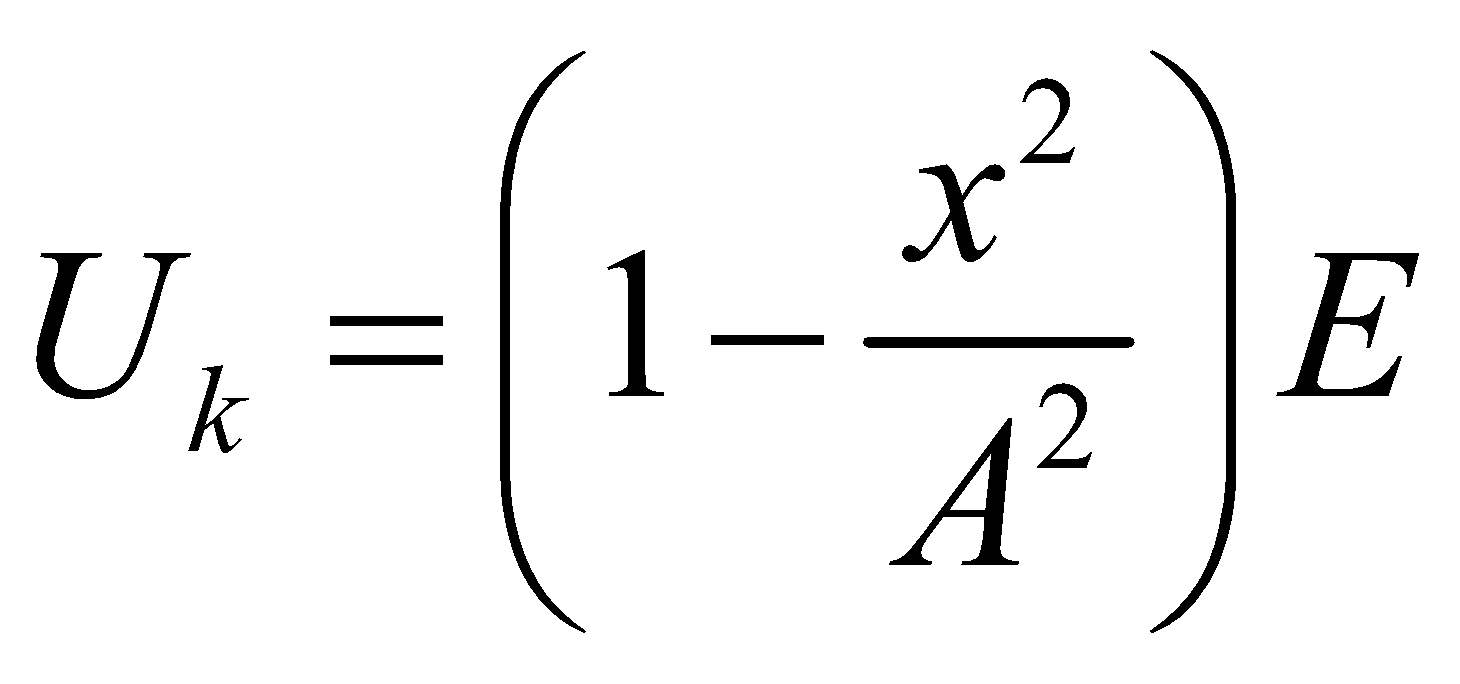
FREE, DAMPED, FORCED OSCILLATIONS AND RESONANCE
FREE OSCILLATION
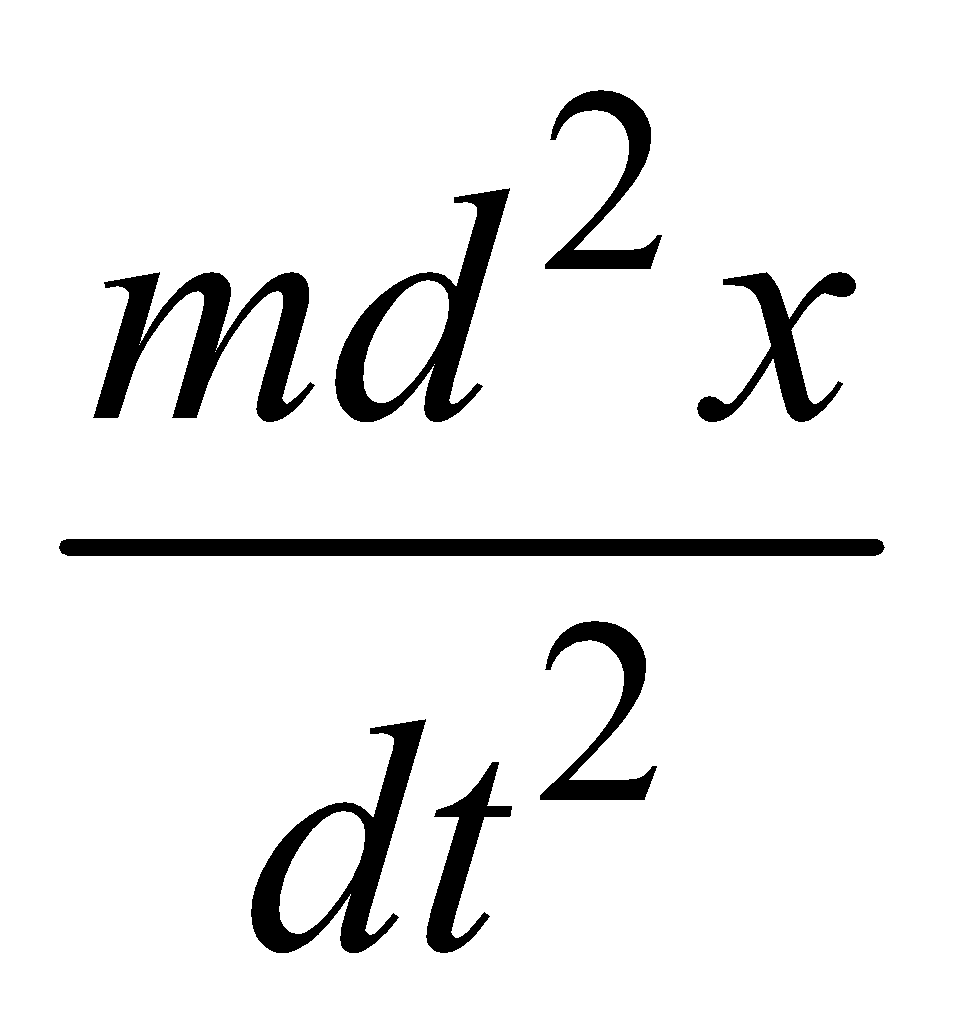 = Frestoring force = –kx, where k is constant.
= Frestoring force = –kx, where k is constant.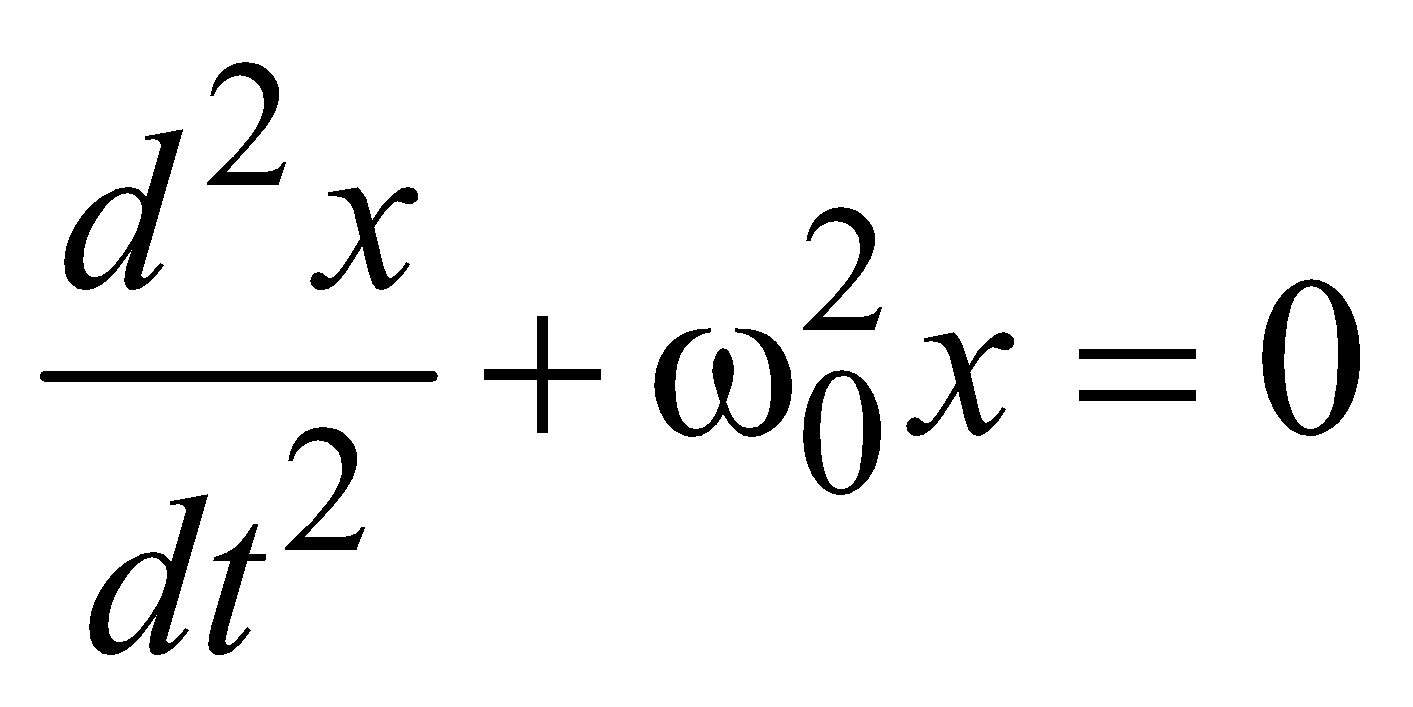 , where ω0 is natural frequency of body.
, where ω0 is natural frequency of body. 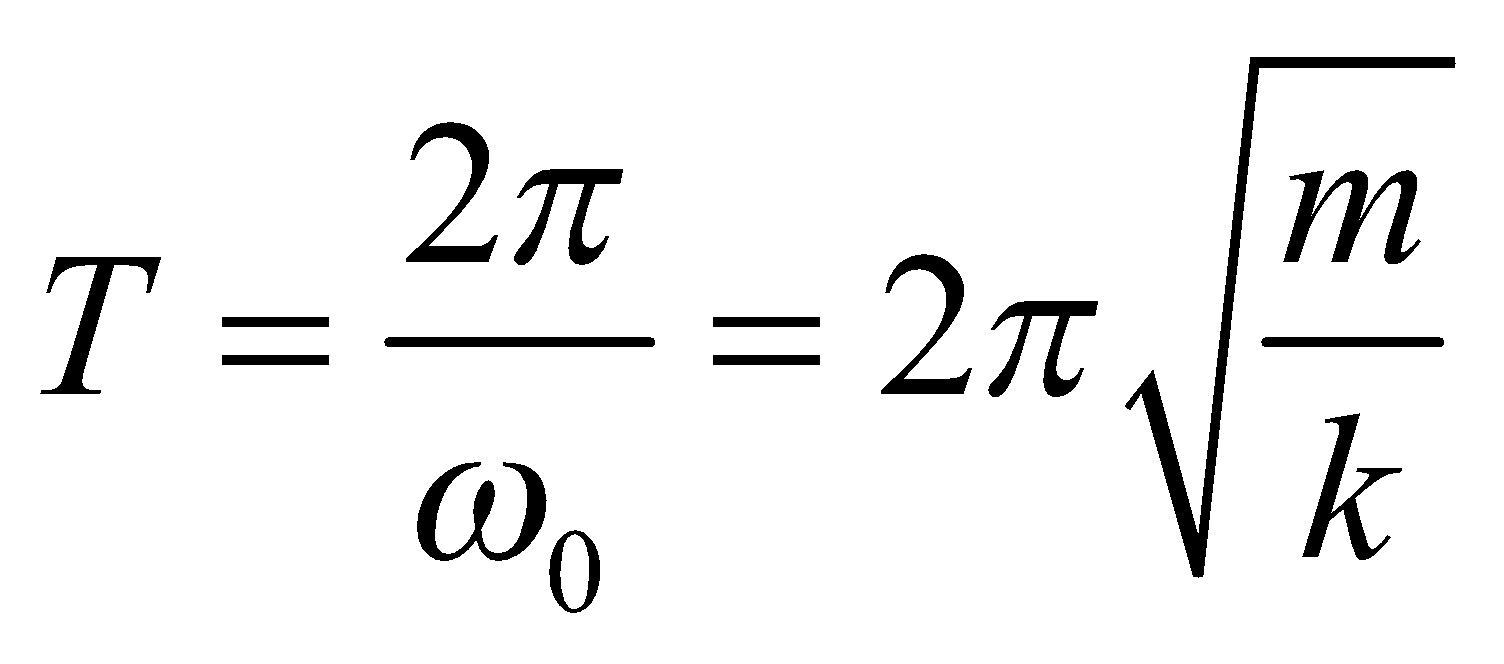
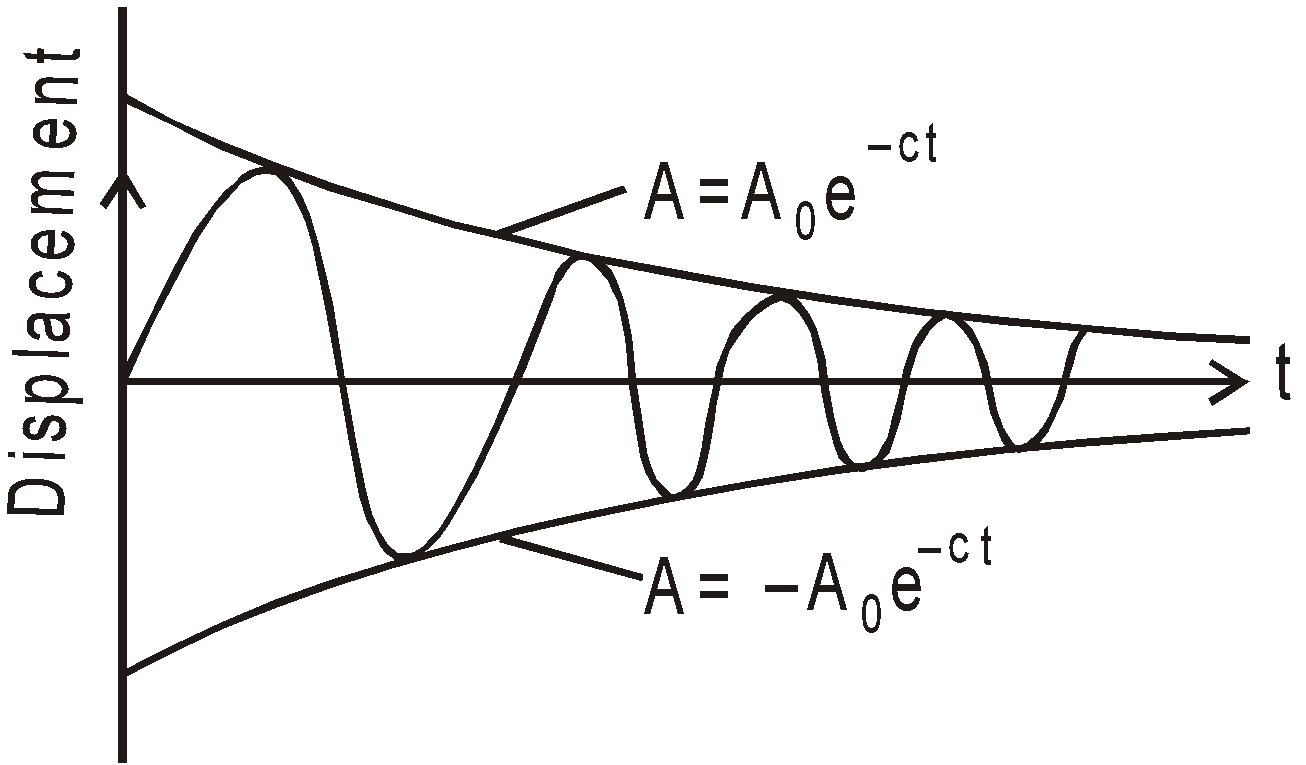
DAMPED OSCILLATION

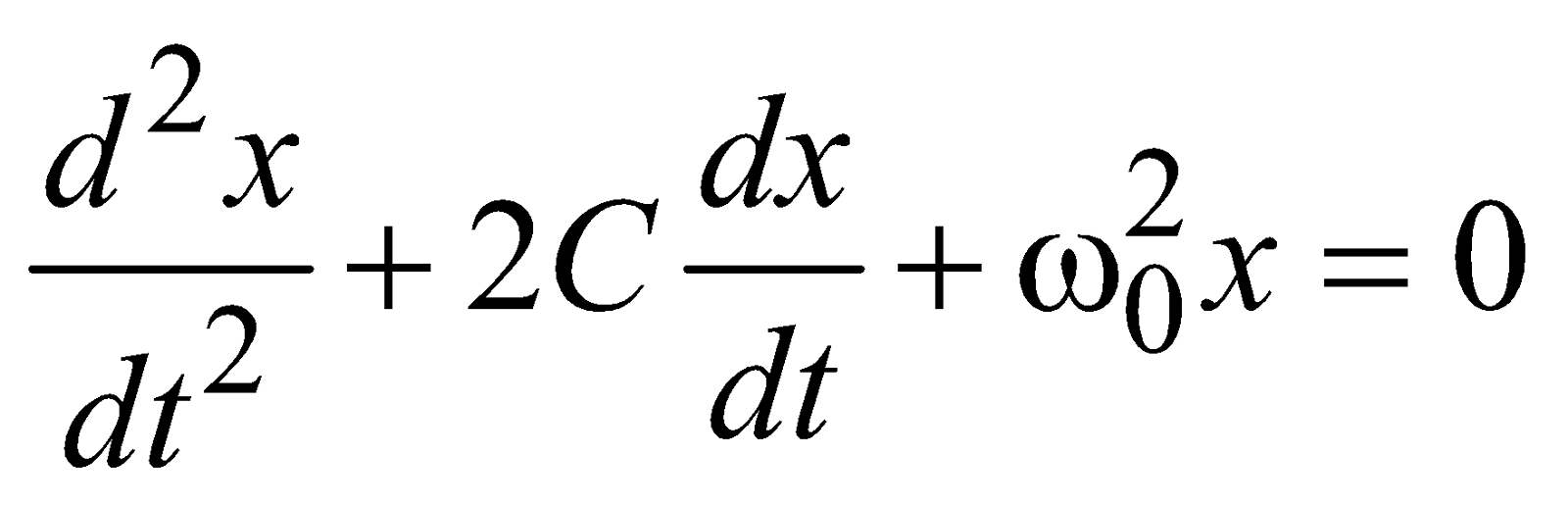 …(i)
…(i)
FORCED OSCILLATION AND RESONANCE
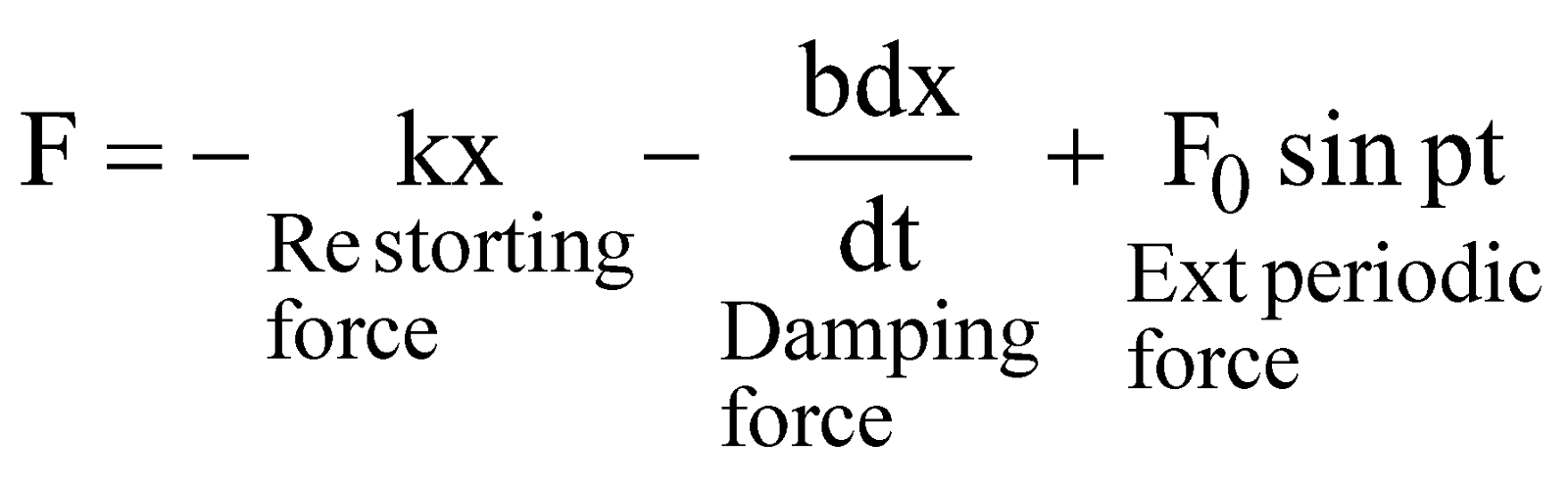 …… (i)
…… (i)