Question
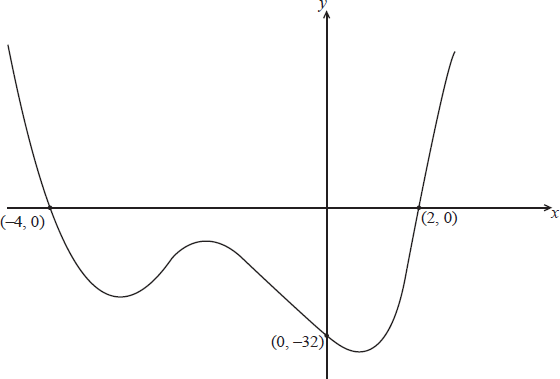
The graph of a polynomial function f of degree 4 is shown below.
Given that \({(x + {\text{i}}y)^2} = – 5 + 12{\text{i}},{\text{ }}x,{\text{ }}y \in \mathbb{R}\) . Show that
(i) \({x^2} – {y^2} = – 5\) ;
(ii) \(xy = 6\) .[2]
Hence find the two square roots of \( – 5 + 12{\text{i}}\) .[5]
For any complex number z , show that \({(z^*)^2} = ({z^2})^*\) .[3]
Hence write down the two square roots of \( – 5 – 12{\text{i}}\) .[2]
Explain why, of the four roots of the equation \(f(x) = 0\) , two are real and two are complex.[2]
The curve passes through the point \(( – 1,\, – 18)\) . Find \(f(x)\) in the form
\(f(x) = (x – a)(x – b)({x^2} + cx + d),{\text{ where }}a,{\text{ }}b,{\text{ }}c,{\text{ }}d \in \mathbb{Z}\) .[5]
Find the two complex roots of the equation \(f(x) = 0\) in Cartesian form.[2]
Draw the four roots on the complex plane (the Argand diagram).[2]
Express each of the four roots of the equation in the form \(r{{\text{e}}^{{\text{i}}\theta }}\) .[6]
Answer/Explanation
Markscheme
(i) \({(x + {\text{i}}y)^2} = – 5 + 12{\text{i}}\)
\({x^2} + 2{\text{i}}xy + {{\text{i}}^2}{y^2} = – 5 + 12{\text{i}}\) A1
(ii) equating real and imaginary parts M1
\({x^2} – {y^2} = – 5\) AG
\(xy = 6\) AG
[2 marks]
substituting M1
EITHER
\({x^2} – \frac{{36}}{{{x^2}}} = – 5\)
\({x^4} + 5{x^2} – 36 = 0\) A1
\({x^2} = 4,\, – 9\) A1
\(x = \pm 2\) and \(y = \pm 3\) (A1)
OR
\(\frac{{36}}{{{y^2}}} – {y^2} = – 5\)
\({y^4} – 5{y^2} – 36 = 0\) A1
\({y^2} = 9,\, – 4\) A1
\({y^2} = \pm 3\) and \(x = \pm 2\) (A1)
Note: Accept solution by inspection if completely correct.
THEN
the square roots are \((2 + 3{\text{i}})\) and \(( – 2 – 3{\text{i}})\) A1
[5 marks]
EITHER
consider \(z = x + {\text{i}}y\)
\(z^* = x – {\text{i}}y\)
\({(z^*)^2} = {x^2} – {y^2} – 2{\text{i}}xy\) A1
\(({z^2}) = {x^2} – {y^2} + 2{\text{i}}xy\) A1
\(({z^2})^* = {x^2} – {y^2} – 2{\text{i}}xy\) A1
\({(z^*)^2} = ({z^2})^*\) AG
OR
\(z^* = r{{\text{e}}^{ – {\text{i}}\theta }}\)
\({(z^*)^2} = {r^2}{{\text{e}}^{ – 2{\text{i}}\theta }}\) A1
\({z^2} = {r^2}{{\text{e}}^{2{\text{i}}\theta }}\) A1
\(({z^2})^* = {r^2}{{\text{e}}^{ – 2{\text{i}}\theta }}\) A1
\({(z^*)^2} = ({z^2})^*\) AG
[3 marks]
\((2 – 3{\text{i}})\) and \(( – 2 + 3{\text{i}})\) A1A1
[2 marks]
the graph crosses the x-axis twice, indicating two real roots R1
since the quartic equation has four roots and only two are real, the other two roots must be complex R1
[2 marks]
\(f(x) = (x + 4)(x – 2)({x^2} + cx + d)\) A1A1
\(f(0) = – 32 \Rightarrow d = 4\) A1
Since the curve passes through \(( – 1,\, – 18)\),
\( – 18 = 3 \times ( – 3)(5 – c)\) M1
\(c = 3\) A1
Hence \(f(x) = (x + 4)(x – 2)({x^2} + 3x + 4)\)
[5 marks]
\(x = \frac{{ – 3 \pm \sqrt {9 – 16} }}{2}\) (M1)
\( \Rightarrow x = – \frac{3}{2} \pm {\text{i}}\frac{{\sqrt 7 }}{2}\) A1
[2 marks]
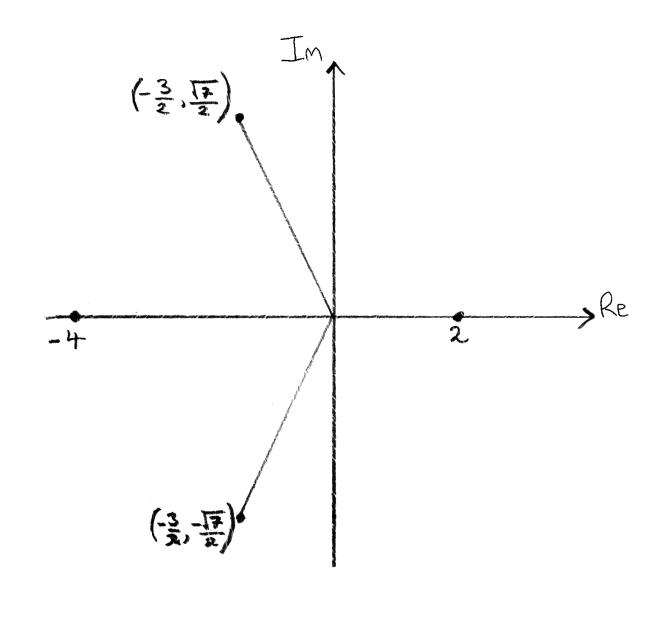 A1A1
A1A1
Note: Accept points or vectors on complex plane.
Award A1 for two real roots and A1 for two complex roots.
[2 marks]
real roots are \(4{{\text{e}}^{{\text{i}}\pi }}\) and \(2{{\text{e}}^{{\text{i}}0}}\) A1A1
considering \( – \frac{3}{2} \pm {\text{i}}\frac{{\sqrt 7 }}{2}\)
\(r = \sqrt {\frac{9}{4} + \frac{7}{4}} = 2\) A1
finding \(\theta \) using \(\arctan \left( {\frac{{\sqrt 7 }}{3}} \right)\) M1
\(\theta = \arctan \left( {\frac{{\sqrt 7 }}{3}} \right) + \pi {\text{ or }}\theta = \arctan \left( { – \frac{{\sqrt 7 }}{3}} \right) + \pi \) A1
\( \Rightarrow z = 2{{\text{e}}^{{\text{i}}\left( {\arctan \left( {\frac{{\sqrt 7 }}{3}} \right) + \pi } \right)}}{\text{ or}} \Rightarrow z = 2{{\text{e}}^{{\text{i}}\left( {\arctan \left( {\frac{{ – \sqrt 7 }}{3}} \right) + \pi } \right)}}\) A1
Note: Accept arguments in the range \( – \pi {\text{ to }}\pi {\text{ or }}0{\text{ to }}2\pi \) .
Accept answers in degrees.
[6 marks]
Question
The quadratic equation \({x^2} – 2kx + (k – 1) = 0\) has roots \(\alpha \) and \(\beta \) such that \({\alpha ^2} + {\beta ^2} = 4\). Without solving the equation, find the possible values of the real number \(k\).
Answer/Explanation
Markscheme
\(\alpha + \beta = 2k\) A1
\(\alpha \beta = k – 1\) A1
\({(\alpha + \beta )^2} = 4{k^2} \Rightarrow {\alpha ^2} + {\beta ^2} + 2\underbrace {\alpha \beta }_{k – 1} = 4{k^2}\) (M1)
\({\alpha ^2} + {\beta ^2} = 4{k^2} – 2k + 2\)
\({\alpha ^2} + {\beta ^2} = 4 \Rightarrow 4{k^2} – 2k – 2 = 0\) A1
attempt to solve quadratic (M1)
\(k = 1,{\text{ }} – \frac{1}{2}\) A1
[6 marks]
Question
Sketch the graphs of \(y = \frac{x}{2} + 1\) and \(y = \left| {x – 2} \right|\) on the following axes.
 [3]
[3]
Solve the equation \(\frac{x}{2} + 1 = \left| {x – 2} \right|\).[4]
Answer/Explanation
Markscheme
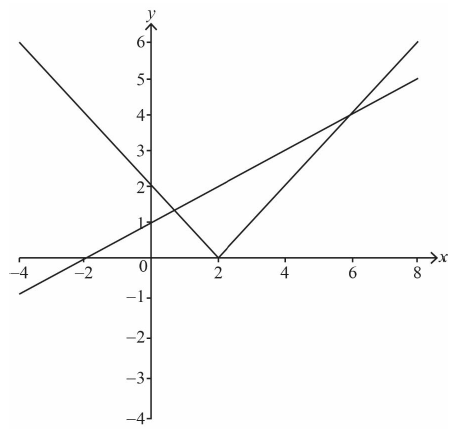
straight line graph with correct axis intercepts A1
modulus graph: V shape in upper half plane A1
modulus graph having correct vertex and y-intercept A1
[3 marks]
METHOD 1
attempt to solve \(\frac{x}{2} + 1 = x – 2\) (M1)
\(x = 6\) A1
Note: Accept \(x = 6\) using the graph.
attempt to solve (algebraically) \(\frac{x}{2} + 1 = 2 – x\) M1
\(x = \frac{2}{3}\) A1
[4 marks]
METHOD 2
\({\left( {\frac{x}{2} + 1} \right)^2} = {\left( {x – 2} \right)^2}\) M1
\(\frac{{{x^2}}}{4} + x + 1 = {x^2} – 4x + 4\)
\(0 = \frac{{3{x^2}}}{4} – 5x + 3\)
\(3{x^2} – 20x + 12 = 0\)
attempt to factorise (or equivalent) M1
\(\left( {3x – 2} \right)\left( {x – 6} \right) = 0\)
\(x = \frac{2}{3}\) A1
\(x = 6\) A1
[4 marks]
Question
A city is concerned about pollution, and decides to look at the number of people using taxis. At the end of the year 2000, there were 280 taxis in the city. After n years the number of taxis, T, in the city is given by\[T = 280 \times {1.12^n} .\]
(i) Find the number of taxis in the city at the end of 2005.
(ii) Find the year in which the number of taxis is double the number of taxis there were at the end of 2000.
At the end of 2000 there were \(25600\) people in the city who used taxis.
After n years the number of people, P, in the city who used taxis is given by\[P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1n}}}} .\](i) Find the value of P at the end of 2005, giving your answer to the nearest whole number.
(ii) After seven complete years, will the value of P be double its value at the end of 2000? Justify your answer.
Let R be the ratio of the number of people using taxis in the city to the number of taxis. The city will reduce the number of taxis if \(R < 70\) .
(i) Find the value of R at the end of 2000.
(ii) After how many complete years will the city first reduce the number of taxis?
Answer/Explanation
Markscheme
(i) \(n = 5\) (A1)
\(T = 280 \times {1.12^5}\)
\(T = 493\) A1 N2
(ii) evidence of doubling (A1)
e.g. 560
setting up equation A1
e.g. \(280 \times {1.12^n} = 560\), \({1.12^n} = 2\)
\(n = 6.116 \ldots \) (A1)
in the year 2007 A1 N3
[6 marks]
(i) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(5)}}}}\) (A1)
\(P = 39635.993 \ldots \) (A1)
\(P = 39636\) A1 N3
(ii) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(7)}}}}\)
\(P = 46806.997 \ldots \) A1
not doubled A1 N0
valid reason for their answer R1
e.g. \(P < 51200\)
[6 marks]
(i) correct value A2 N2
e.g. \(\frac{{25600}}{{280}}\) , 91.4, \(640:7\)
(ii) setting up an inequality (accept an equation, or reversed inequality) M1
e.g. \(\frac{P}{T} < 70\) , \(\frac{{2560000}}{{(10 + 90{{\rm{e}}^{ – 0.1n}})280 \times {{1.12}^n}}} < 70\)
finding the value \(9.31 \ldots \) (A1)
after 10 years A1 N2
[5 marks]